1.本发明涉及航天器姿态确定控制技术领域，具体涉及一种卫星在轨自主立体成像姿态规划方法。


背景技术：

2.立体成像是卫星数据获取模式的一种，利用卫星俯仰轴的快速姿态机动来实现同轨多次对同一地面目标不同角度的观测，专用立体成像测绘卫星采用多线阵相机直接进行立体成像，可进行连续长条带成像，但经济成本高和研制难度大，相应卫星体积大。敏捷卫星只有一个相机，体积小、重量轻，通过整星姿态快速机动和快速稳定控制实现同轨立体成像和异轨立体成像。同轨立体成像与异轨立体成像相比缩短了立体像对的获取时间间隔，避免了成像时间差过大，地物、大气、光照条件变化造成的影像差异等现象，方便测图处理，是目前的发展趋势。
3.现有对立体成像的研究较少，采用的基本为平面地球模型或圆形地球模型，同时为简化分析过程，不考虑地球椭率和自转的影响，也不考虑滚动方向的姿态机动，与实际情况存在偏差。多数研究算法采用搜索策略，遍历计算全部可行的前后视成像时间窗口，进行成像窗口的选取，不适用于在轨实时规划。
4.受matlab、stk等国外软件对国内用户限制的影响，给立体成像任务的规划增加了难度，有必要设计一种采用椭球地球模型，并考虑地球的自转以及滚动方向的机动的立体成像规划方案，提高规划的精度。


技术实现要素：

5.本发明为解决现有立体成像任务的规划增加了难度以及不适用于在轨实时规划等问题，提供一种卫星在轨自主立体成像姿态规划方法。
6.一种卫星在轨自主立体成像姿态规划方法，该方法通过卫星成像姿态求解、成像时间窗口确定和成像时长确定三个步骤实现；该方法的具体步骤如下：
7.步骤一、卫星成像姿态求解；
8.将卫星的实时位置、实时速度和成像点的经度、纬度和高度以及地球自转角速度作为卫星成像姿态求解的输入，定义卫星成像时的姿态对应的本体系指向为期望坐标系，得到轨道系相对期望坐标系的旋转四元数
[0009][0010]
式中，为旋转轴旋转角度，为旋转轴向量在轨道坐标系下的表示形式；
[0011]
步骤二、成像时间窗口确定；包括对双视成像模式和三视成像模式成像时间窗口的确定；
[0012]
所述三视成像时间窗口方法为：
[0013]
步骤a、设定卫星前视、正视和后视成像时间初值分别为t1、t2和t3，且t1＝t2＝t3
＝max，max＝10
20
，初始时间time＝t0；
[0014]
步骤b、通过轨道递推得到时间time对应的卫星位置和速度信息；
[0015]
步骤c、由卫星位置、速度信息、成像点的经纬高以及地球自转角速度，经过卫星成像姿态求解，获得初始时间time对应的旋转角度在卫星飞行方向的分量
[0016]
步骤d、判定初始时间time，如果time＜t1，则执行步骤d1；
[0017]
如果t1＜time＜t2，则执行步骤d2；
[0018]
如果t2＜time＜t3，则执行步骤d3；
[0019]
步骤d1、判断如果成立，获取对应的前视成像时间t01与成像姿态q
f1
，修改成像时间值t1＝t01，执步骤e，否则，直接执行步骤e；
[0020]
步骤d2、判断如果成立，获取对应的正视成像时间t02与成像姿态q
f2
，修改成像时间值t2＝t02，执步骤e，否则，直接执行步骤e；
[0021]
步骤d3、判断如果成立，获取对应的后视成像时间t03与成像姿态q
f3
，执行步骤f，否则，执行步骤e；
[0022]
步骤e、增加递推时间δt，time＝time+δt，进行轨道递推，返回执行步骤b；
[0023]
步骤f、成像姿态求解结束，输出结果；
[0024]
所述双视成像时间确定获取过程中，需要对前视与后视两个角度的判定，通过前视成像时要求后视成像时最终获取对应的前视成像时间t04与期望姿态q
f4
，后视成像时间t05与期望姿态q
f5
；
[0025]
步骤三、成像时长确定；
[0026]
根据步骤二中对三视成像时间窗口和双视成像时间窗口的确定，对卫星是否能进行相应的成像及成像时长的判定如下：
[0027]
通过三视成像，计算成像时长如果则进行三视成像，且成像时长为否则，不进行三视成像；
[0028]
通过双视成像，计算成像时长如果则进行双视成像，且成像时长为否则，不进行双视成像。
[0029]
本发明的有益效果：
[0030]
本发明采用立体成像策略，实现卫星的在轨自主姿态规划。同时，拼接成像为相机在短时间内获取多幅包含一定重叠区域的图像的成像模式，其工作原理与立体成像类似，针对两种成像模式的双视、三视两种情形进行成像策略设计。
[0031]
通过本发明的卫星在轨自主立体成像姿态规划后，采用椭球地球模型，并考虑地球的自转以及卫星滚动方向影像的立体成像规划方法，提高立体成像的姿态确定精度并获取成像时长。从而提高低轨遥感卫星的成像能力，确保了在轨采集的图像数据的准确性。
附图说明
[0032]
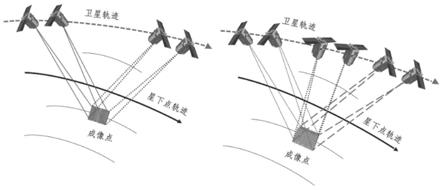
图1为立体成像双视/三视示意图；
[0033]
图2为拼接成像双视/三视示意图；
[0034]
图3为卫星位置与成像点关系示意图；
[0035]
图4为卫星姿态求解流程图；
[0036]
图5为双视飞行方向成像与机动示意图；
[0037]
图6为三视飞行方向成像与机动示意图；
[0038]
图7为三视成像时间窗口确定流程图；
[0039]
图8为双视成像时间窗口确定流程图；
[0040]
图9为卫星与成像点示例效果图；
[0041]
图10为北京市拼接三视姿态角效果图；
[0042]
图11为北京市拼接三视角速度效果图；
[0043]
图12为上海市立体双视姿态角效果图；
[0044]
图13为上海市立体双视角速度效果图。
具体实施方式
[0045]
结合图1至图13说明本实施方式，一种卫星在轨自主立体成像姿态规划方法，该方法涉及的相关定义如下：
[0046]
1、相关坐标系定义；
[0047]
本发明中使用了本体坐标系o
b
x
b
y
b
z
b
，轨道坐标系o
b
x
o
y
o
z
o
，惯性系c
e
x
ei
y
ei
z
ei
和地固系c
e
x
e
y
e
z
e
四种坐标系。
[0048]
(1)本体坐标系o
b
x
b
y
b
z
b
：坐标原点o
b
位于卫星质心处，三轴指向与星体安装有关，定义x
b
轴指向帆板方向，z
b
轴指向相机方向，y
b
轴与x
b
轴和z
b
轴构成右手直角坐标系。
[0049]
(2)轨道坐标系o
b
x
o
y
o
z
o
：坐标原点为卫星质心o
b
，y轴指向轨道角速度反方向，z
o
轴指向地球中心，x
o
轴与y
o
轴和z
o
轴构成右手直角坐标系(飞行方向)，此坐标系为对地定向基准。
[0050]
(3)惯性系c
e
x
ei
y
ei
z
ei
：坐标系原点为地球质心c
e
，x
ei
轴指向平春分点(2000年1月1日12时)，z
ei
轴指向平北极(2000年1月1日12时，jd＝2451545.0)，y
ei
轴和x
ei
轴、z
ei
轴构成右手直角坐标系，也称j2000地球惯性坐标系。
[0051]
(4)地固系c
e
x
e
y
e
z
e
：坐标原点为地球质心c
e
，z
e
轴指向国际时间局1984.0定义的协议地极方向，x
e
轴指向1984.0的协议子午面和赤道的交点，y
e
轴与z
e
轴、x
e
轴垂直构成右手坐标系，也称wgs84地球固连坐标系。
[0052]
2、本发明中卫星姿态采用四元数形式进行描述，相关性质定义如下：
[0053]
卫星姿态的描述方式，四元数表示：其中其中
[0054]
q0为四元数的标部，代表旋转角φ，为四元数的矢部，代表旋转轴的方向e
n
＝[i；j；k],满足i2+j2+k2＝1。
[0055]
四个参数满足约束方程：
[0056]
矢量乘积规则：
[0057][0058]
四元数的逆：
[0059]
四元数乘法：
[0060]
本实施方式所述的一种卫星在轨自主立体成像姿态规划方法的具体步骤如下：
[0061]
步骤一、卫星成像姿态求解；
[0062]
首先，采用椭球形地球模型，考虑地球椭率的影响，由成像点的经纬高(经度：lon(rad)，纬度：lat(rad)，高度：h(km))信息，根据公式求得在地固系下的位置向量p＝[p
x
；p
y
；p
z
](km)，其中r(km)为赤道半径，e为偏心率。
[0063]
通过卫星的导航数据和轨道递推公式递推得到在地固系下表示的的实时位置向量为s＝[s
x
；s
y
；s
z
](km)，对应的单位向量为e
s
＝e(s)，沿轨道系z
o
轴反方向，如图3，其中||
·
||2为求向量的模值。实时速度向量为v＝[v
x
；v
y
；v
z
](km/s)。
[0064]
在地固系之下，地球自转角速度ω＝[0；0；ω
e
](rad/s),ω
e
＝(7.292115
±
0.00000015)
×
10
‑5(rad/s)。考虑地球自转的影响，卫星的合成速度为：v
s
＝v+(ω
×
s)，其对应的单位向量为
[0065]
然后，由卫星的位置、速度和成像点的经纬高以及地球自转角速度作为输入，进行卫星的姿态求解，求解流程如图4所示，姿态求解公式如下：
[0066]
c
e
,p,s三点共面，如图3，c
e
为地球质心，定义向量k＝s
‑
p为卫星成像时相机指向，e
k
＝e(k)，平面c
e
ps的法线方向的向量在地固系的表示n＝e
s
×
e
k
，e
n
＝e(n)。
[0067]
由欧拉旋转定理知，向量e
s
以向量e
n
为旋转轴旋转角度得到向量e
k
，旋转角度由求解得到。
[0068]
卫星的前后视角度是相对于轨道系定义的，因此需要计算旋转轴在轨道系下的表示e
n
o，根据轨道系的定义，由向量s,k,n,v
s
计算轨道坐标系三轴在地固系表示的向量根据向量在坐标系中的表示公式可以解得的三轴分量为
旋转角在轨道系三轴分量为
[0069]
定义卫星成像时的姿态对应的本体系指向为期望坐标系，轨道系相对期望系的旋转四元数为
[0070]
步骤二、成像时间窗口确定；
[0071]
本实施方式中，卫星进行立体成像与拼接成像的区别在于两次/三次拍摄的是否为同一个目标点，当沿卫星飞行方向进行分析时，无侧摆方向的影响，两种成像模式是一致的。
[0072]
双视模式的卫星成像过程分为前视与后视两部分，如图5所示，在a1至a2段进行时长t
image
的前视角度θ的成像；在b1至b2段进行时长t
image
的后视角度θ的成像；a2至b1段为时长t
trans
的前视到后视转换的姿态机动及稳定段。双视成像的成像与机动时间关系如表1所示。
[0073]
表1双视成像与机动时间关系表
[0074]
成像/机动时间段成像时长机动时长前视角度θ的成像a1
‑
a2t
image
/前视转后视a2
‑
b1/t
trans
后视角度
‑
θ的成像b1
‑
b2t
image
/
[0075]
在前视与后视角度θ确定后，a1至b1段对应的时间t
trans
+t
image
是确定的，当卫星的机动能力增强时，t
trans
时间减小为t
trans
‑
δt，对应的成像时间增加为t
image
+δt。
[0076]
三视模式的卫星成像过程分为前视、正视与后视三部分，如图6所示，在a1至a2段进行时长t
image
的前视角度为θ的成像；在b1至b2段进行正视的成像，成像时长t
image
；在c1至c2段进行时长t
image
的后视角度为θ的成像；a2至b1段为时长t
trans1
的前视到正视转换的姿态机动及稳定段；b2至c1段为时长t
trans2
的正视到后视转换的姿态机动及稳定段。三视成像的成像与机动时间关系如表2所示。
[0077]
表2三视成像与机动时间关系表
[0078]
成像/机动时间段成像时长机动时长前视角度θ的成像a1
‑
a2t
image
/前视转正视a2
‑
b1/t
trans1
正视角度0的成像b1
‑
b2t
image
/正视转后视b2
‑
c1/t
trans2
后视角度
‑
θ的成像c1
‑
c2t
image
/
[0079]
由于成像时前视和后视角度的存在，卫星的成像窗口时间并非对成像点的过境时间窗口，需要根据前后视的角度进行反向求解获取。三视成像时间窗口确定流程图如图7，获取过程如下：
[0080]
步骤a、设定卫星前视、正视和后视成像时间初值分别为t1、t2和t3，且t1＝t2＝t3＝max，max＝10
20
，初始时间time＝t0；
[0081]
步骤b、通过轨道递推得到时间time对应的卫星位置和速度信息；
[0082]
步骤c、由卫星位置、速度信息、成像点的经纬高以及地球自转角速度，经过卫星成像姿态求解，获得初始时间time对应的旋转角度在卫星飞行方向的分量
[0083]
步骤d、判定初始时间time，如果time＜t1，则执行步骤d1；
[0084]
如果t1＜time＜t2，则执行步骤d2；
[0085]
如果t2＜time＜t3，则执行步骤d3；
[0086]
步骤d1、判断如果成立，获取对应的前视成像时间t01与成像姿态q
f1
，修改成像时间值t1＝t01，执步骤e，否则，直接执行步骤e；
[0087]
步骤d2、判断如果成立，获取对应的正视成像时间t02与成像姿态q
f2
，修改成像时间值t2＝t02，执步骤e，否则，直接执行步骤e；
[0088]
步骤d3、判断如果成立，获取对应的后视成像时间t03与成像姿态q
f3
，执行步骤f，否则，执行步骤e；
[0089]
步骤e、增加递推时间δt，time＝time+δt，进行轨道递推，返回执行步骤b；
[0090]
步骤f、成像姿态求解结束，输出结果；
[0091]
双视成像时间确定获取过程中，只有前视与后视两个角度的判定，通过前视成像时要求后视成像时最终获取对应的前视成像时间t04与期望姿态q
f4
，后视成像时间t05与期望姿态q
f5
。
[0092]
如图8所示，双视成像时间确定获取的流程为：
[0093]
步骤a、设定卫星前视、后视成像时间初值分别为t4和t5，且t4＝t5＝max，max＝10
20
，初始时间time＝t0；
[0094]
步骤b、通过轨道递推得到时间time对应的卫星位置和速度信息；
[0095]
步骤c、由卫星位置、速度信息、成像点的经纬高以及地球自转角速度，经过卫星成像姿态求解，获得初始时间time对应的旋转角度在卫星飞行方向的分量
[0096]
步骤d、判定初始时间time，如果time＜t4，则执行步骤d1；
[0097]
如果t4＜time＜t5，则执行步骤d2；
[0098]
步骤d1、判断如果成立，获取对应的前视成像时间t04与成像姿态q
f4
，修改成像时间值t4＝t04，执步骤e，否则，直接执行步骤e；
[0099]
步骤d2、判断如果成立，获取对应的后视成像时间t05与成像姿态q
f5
，执行步骤f，否则，执行步骤e；
[0100]
步骤e、增加递推时间δt，time＝time+δt，进行轨道递推，返回执行步骤b；
[0101]
步骤f、成像姿态求解结束，输出结果。
[0102]
步骤三：成像时长确定；
[0103]
三视成像中，由步骤二中三视成像的期望姿态可得，前视至正视的姿态转换四元数为正视至后视的姿态转换四元数为
[0104]
双视成像中，由步骤二中两次成像的期望姿态可得，前视至后视的姿态转换四元数为
[0105]
在满足卫星转动惯量i、反作用飞轮力矩t和角动量h约束下，通过对卫星的控制，卫星的机动能力越强，姿态旋转q
e1
、q
e2
、q
e3
所需要的机动时间t
trans1
、t
trans2
、t
trans3
越短，卫星的建模与控制如下。
[0106]
刚体卫星的动力学与运动学方程描述为：刚体卫星的动力学与运动学方程描述为：其中，u为控制力矩，s(
·
)为反对称矩阵，
[0107]
采用pd控制器对卫星机型控制：u＝
‑
k
p
q
e
‑
k
d
ω
e
，其中，k
p
,k
d
分别为比例控制增益矩阵和微分控制增益矩阵，k
p
＝k
p
i,k
d
＝k
d
i,增益矩阵系数k
p
＞0,k
d
＞0。
[0108]
其中，偏差角速度ω
e
＝ω
‑
r(q
e
)ω
gui
，ω
gui
为轨道角速度，卫星角速度ω为卫星本体系相对惯性系的转动角速度,r(q
e
)为q
e
对应的旋转矩阵，偏差四元数q
e
在双视和三视控制中分别为q
e1
，q
e2
和q
e3
。
[0109]
由步骤二中的成像时间窗口确定可得卫星成像时长与卫星机动时间的对应关系为：
[0110]
三视成像两次机动时间t
trans1
和t
trans2
以及成像时间t
image
与成像确定时间t01、t02和t03的对应关系为：t
trans1
+t
image
＝t02
‑
t01，t
trans2
+t
image
＝t03
‑
t02。
[0111]
双视成像的机动时间t
trans3
和成像时间t
image3
与成像确定时间t04和t05的对应关系为：t
trans3
+t
image3
＝t05
‑
t04。
[0112]
考虑卫星成像数据的处理需求，要求卫星成像时长≥4s，因此，卫星是否能进行相应的成像及成像时长的判定如下：
[0113]
三视成像中计算的可成像时长如果可进行三视成像，且成像时长为否则不可进行三视成像。其中(x,y)
min
为求x,y的最小值。
[0114]
双视成像中计算的可成像时长如果可进行双视成像，且成像时长为否则不可进行双视成像。
[0115]
具体实施方式二、结合图9至图13说明本实施方式，本实施方式为具体实施方式一所述的一种卫星在轨自主立体成像姿态规划方法的实施例：
[0116]
成像时间窗口与期望四元数验证；
[0117]
采用轨道高度为535km，降交点地方时为11:00的太阳同步轨道卫星进行仿真验证，考虑卫星的幅宽为40km，并且拼接成像时具有>10％的图像重叠率，由此获取拼接成像的成像点的经纬度信息，对成像点为上海市经纬度[121.368
°
；31.1094
°
]的双视立体与拼接成像、成像点为北京市经纬度[116.388
°
；39.9289
°
]的三视立体与拼接成像进行仿真，如图9，前后视角度θ＝25
°
的成像时间窗口与期望四元数计算结果如表1
‑
4。表1成像点上海的立体双视成像时间窗口与期望四元数信息表，表2成像点上海的拼接双视成像时间窗口与期望四元数计算，表3成像点北京的立体三视成像时间窗口与期望四元数计算，表4成像点
北京的拼接三视成像时间窗口与期望四元数计算。
[0118]
表1
[0119][0120]
表2
[0121][0122][0123]
表3
[0124][0125]
表4
[0126][0127]
[0128]
本实施方式中，还包括对成像时长进行验证：
[0129]
卫星转动惯量飞轮力矩t＝[0.01；0.01；0.01]n
·
m；飞轮角动量h＝[0.2；0.2；0.2]n
·
m
·
s；卫星初始姿态q
c
＝[0.257979；0.208206；0.943371；0.012177]；初始角速度ω
c
＝[0；0；0]
°
/s。
[0130]
上海双视立体成像在仿真时间time＝292.92s时进行旋转四元数q
esh
＝[0.906599；0.022058；
‑
0.417518；0.057173]的机动。
[0131]
上海双视拼接成像在仿真时间time＝292.92s时进行旋转四元数q
esh1
＝[0.906745；
‑
0.005242；
‑
0.418525；0.051217]的机动。
[0132]
北京三视立体成像在仿真时间time＝294.78s时进行旋转四元数q
ebj1
＝[0.976765；
‑
0.004954；
‑
0.207279；
‑
0.05423]的机动，在仿真时间time＝335.56s时进行旋转四元数q
ebj2
＝[0.976445；0.022716；
‑
0.207583；
‑
0.054311]的机动。
[0133]
北京三视拼接成像在仿真时间time＝294.78s时进行旋转四元数q
ebj3
＝[0.976634；0.017028；
‑
0.208421；
‑
0.049546]的机动，在仿真时间time＝334.93s时进行旋转四元数q
ebj4
＝[0.975391；0.047685；
‑
0.209429；
‑
0.049787]的机动。
[0134]
北京拼接三视姿态角与角速度如图10
‑
图11所示，上海立体双视姿态角与角速度如图12
‑
图13所示。成像时长与机动完成时间统计如表5，表5为成像时长与机动完成时间统计表。
[0135]
表5
[0136][0137]
前后视25
°
的上海立体双视成像的成像时长为25s，上海立体拼接成像的成像时长为25s。北京立体三视成像的成像时长为7s，上海立体拼接成像的成像时长为5s。