1.本发明涉及一种航天器姿态/故障/干扰协同观测与容错抗干扰控制方法,特别涉及多源复杂扰动下航天器姿态高精高稳控制方法。
背景技术:
2.近年来,航天器高精度姿态稳定控制为空间交会对接、在轨装配、在轨抓捕等空间技术提供了理论基础。然而在实际操作中,由于存在外界干扰、测量误差、执行机构故障及饱和受限等复杂情形,传统控制方法不能保证任务精确实施,甚至导致空间任务的失败。特别是,现有所涉及到的状态观测器仅能估计系统状态;干扰状态观测器仅能估计系统综合干扰或者估计系统状态与干扰信息,将执行机构故障作为综合干扰的一个来源,并不详细考虑;容错控制器多数只针对故障检测或者干扰抑制其一展开的。
3.当外界干扰、测量误差、执行机构故障同时存在于航天器姿态控制系统,且姿态信息未知时,传统容错控制或抗干扰控制方法将不能详细考虑执行机构故障和外界干扰各自对姿控系统的影响机理,导致相关容错控制或抗干扰控制理论失效。如何实时地对多源复杂扰动进行估计补偿,从而实现航天器高精高稳控制,对于航天器长期在轨工作并完成复杂空间任务具有重要的理论意义和应用价值,这也是本发明所要解决的重要问题。
技术实现要素:
4.本发明的目的是提供一种航天器姿态/故障/干扰协同观测与容错抗干扰控制方法,实时地进行外界干扰的估计和执行机构故障的检测,以实现航天器高精度姿态稳定控制。
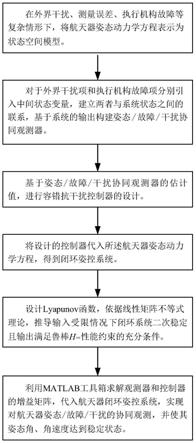
5.一种航天器姿态/故障/干扰协同观测与容错抗干扰控制方法包括以下步骤:
6.步骤一:在外界干扰、测量误差、执行机构故障及饱和受限等复杂情形下,将航天器姿态动力学方程表示为状态空间模型:
7.定义θ,ψ分别代表航天器的滚转角、俯仰角和偏航角,表示轨道角速度,w(t)表示外界干扰,v(t)表示测量误差,f(t)表示执行机构故障,记表示外界干扰,v(t)表示测量误差,f(t)表示执行机构故障,记u(t)=[t
cx t
cy t
cz
]
t
,假设航天器在圆轨道上运行,其本体坐标系为惯性主轴坐标系,航天器能提供沿三个坐标轴方向互相垂直的控制力矩,在小角度条件下,航天器的姿态动力学模型可表示为:
[0008]
[0009][0010][0011]
其中,i
x
,i
y
,i
z
表示三轴方向惯性矩阵的分量,表示三轴方向控制力矩,为对应的分布矩阵系数,当航天器执行机构发生故障时有
[0012]
步骤二:对于外界干扰项和执行机构故障项分别引入中间状态变量,建立两者与系统状态之间的联系,并基于系统的输出构建姿态/故障/干扰协同观测器:
[0013]
定义变量ε和ξ具有如下形式:
[0014][0015]
记为x(t),y(t),ε(t),ξ(t),w(t),f(t)的估计值,l是状态观测器的增益矩阵,则姿态/故障/干扰协同观测器具有如下形式:
[0016][0017]
从而实现对干扰和故障信号的重构:
[0018][0019]
步骤三:基于航天器姿态/故障/干扰协同观测器的估计值,进行容错抗干扰控制器的设计:
[0020]
定义为列满秩矩阵,记为的penrose逆矩阵,利用系统状态、外界干扰、执行机构故障的估计值,设计具有如下形式的控制器:
[0021][0022]
其中,k是状态反馈增益矩阵,分别代表外界干扰补偿项和执行机构故障补偿项。
[0023]
步骤四:将设计的控制器代入步骤一所述航天器姿态动力学状态空间t
cx
,t
cy
,t
cz
模型,得到闭环姿态控制系统模型:
[0024]
定义观测误差具有如下形式:
[0025][0026]
记总扰动扩展状态则可以得到闭环系统状态方程:
[0027][0028]
其中,
[0029][0030]
步骤五:设计lyapunov函数,依据线性矩阵不等式理论,推导输入受限情况下闭环系统二次稳定且输出满足鲁棒h
∞
性能约束的充分条件:
[0031]
对于实际在轨运行的航天器,其执行机构存在饱和上限,对于任意轴向的控制力矩应存在以下约束:
[0032]
u
i
(t)=sign(u
i
(t))min{u
i
(t)|,u
i max
}(i=x,y,z)
[0033]
其中,u
i max
为控制力矩的幅值。
[0034]
设计lyapunov函数
[0035][0036]
对于给定p0>0,τ
i
>0(i=1,2),κ
s
>0(s=1,2),k0>0,假设存在对称正定矩阵p1,p2,p3,p4和正常数γ,若闭环系统在步骤三所述的控制器作用下具有步骤五所述的二次稳定性并且输出满足鲁棒h
∞
性能约束,则在输入受限情况下,矩阵k和h可以通过求解以下线性矩阵不等式组得到:
[0037]
p0(a
‑
b1k)+(a
‑
b1k)
t
p0<0
[0038]
[0039][0040][0041]
其中,
[0042][0043][0044][0045][0046][0047][0048][0049][0050]
h=p2l
[0051][0052]
由矩阵p2和h,可以得到观测器增益矩阵
[0053]
步骤六:利用matlab工具箱求解观测器和控制器的增益矩阵,代入航天器闭环姿态控制系统,实现对航天器姿态/故障/干扰的协同观测,并使其姿态角、角速度达到稳定状态:
[0054]
利用matlab工具箱的线性矩阵不等式求解器对于步骤五所述的不等式组进行求解,可以得到控制器增益矩阵k和观测器增益矩阵l,代入步骤四所描述的闭环姿态控制系统模型,可实现航天器的容错抗干扰姿态稳定控制。
[0055]
本发明的有益效果为:
[0056]
与现有技术相比,本发明的有益效果是在测量误差、外界干扰、执行机构故障及饱和受限等复杂情形下,能够对外界干扰和执行机构故障信号分别进行实时估计,利用所设计的容错抗干扰控制方法能够使航天器姿态快速高精度地达到稳定状态,稳定时间大约
15s,姿态角控制精度小于10
‑3rad,姿态角速度控制精度小于10
‑4rad/s,整个控制过程,控制力矩最大不超过1nm。
[0057]
本发明设计的姿态/故障/干扰协同观测与容错抗干扰控制方法,针对多源扰动作用下航天器姿态控制问题,能够实时地实现外界干扰和故障信号的估计,使得在多源扰动影响下的航天器能够快速高精度的达到稳定状态。
附图说明
[0058]
图1为本发明一种航天器姿态/故障/干扰协同观测与容错抗干扰控制方法的流程图;
[0059]
图2为本发明中在容错抗干扰控制器的作用下,航天器闭环姿态系统姿态角的变化曲线,θ,ψ分别代表航天器滚转角、俯仰角和偏航角,rad表示角度的单位为弧度;
[0060]
图3为本发明中在容错抗干扰控制器的作用下,航天器闭环姿态系统姿态角速度的变化曲线,ω
x
,ω
y
,ω
z
.表示姿态角速度的三轴分量,rad/s表示角速度的单位为弧度/秒;
[0061]
图4为本发明中基于姿态/故障/干扰协同观测器对于执行机构故障的观测变化曲线,f
x
,f
y
,f
z
为三轴执行机构故障信号的预设值,为故障信号f
x
,f
y
,f
z
的估计值,nm表示故障信号的单位为牛米;
[0062]
图5为本发明中基于姿态/故障/干扰协同观测器对于外界干扰的观测变化曲线,w
x
,w
y
,w
z
为三轴外界干扰的预设值,为干扰信号w
x
,w
y
,w
z
的估计值,nm表示干扰信号的单位为牛米;
[0063]
图6为本发明中容错抗干扰控制器控制力矩大小变化曲线,u
x
,u
y
,u
z
是控制力矩对应的三轴分量,nm表示控制力矩的单位为牛米。
[0064]
具体实施方法:
[0065]
结合附图和具体实施例对本发明进行进一步说明:
[0066]
本实施例一种航天器姿态/故障/干扰协同观测与容错抗干扰控制方法具体是按照以下步骤实现的:
[0067]
航天器在轨道高度h=400km的圆轨道运行,地球半径r=6371km;
[0068]
航天器惯性参数i
x
=20kg
·
m2,i
y
=18kg
·
m2,i
z
=15kg
·
m2;
[0069]
外界干扰外界干扰是轨道角速度;
[0070]
测量误差v(t)=10
‑4×
[4rad 5rad 6rad 0.2rad/s 0.2rad/s 0.2rad/s]
t
sin(0.01πt);
[0071]
执行机构故障信号f(t)=[0.01 0.011 0.009]
t
f0(t),其中f0(t)具有如下的分段形式:
[0072][0073]
步骤一:在外界干扰、测量误差、执行机构故障等复杂情形下,将航天器姿态动力学方程表示为状态空间模型。
[0074]
定义θ,ψ分别代表航天器滚转、俯仰和偏航三个姿态角记u(t)=[t
cx t
cy t
cz
]
t
,其本体坐标系为惯性主轴坐标系,航天器能提供沿三个坐标轴方向互相垂直的控制力矩,在小角度条件下,航天器的姿态动力学模型可表示为:
[0075][0076][0077][0078]
其中,t
cx
,t
cy
,t
cz
表示三轴方向控制力矩,为对应的分布矩阵系数,当航天器执行机构发生故障时有
[0079]
步骤二:针对外界干扰项和执行机构故障项引入双中间状态变量,并基于此构建姿态/故障/干扰协同观测器。
[0080]
定义变量ε和ξ具有如下形式:
[0081][0082]
记为x(t),y(t),ε(t),ξ(t),w(t),f(t)的估计值,l是状态观测器的增益矩阵,则姿态/故障/干扰协同观测器具有如下形式:
[0083][0084]
可实现对干扰和故障信号的重构:
[0085][0086]
步骤三:利用姿态/故障/干扰协同观测器的输出,设计容错抗干扰控制器。
[0087]
定义为列满秩矩阵,记为的penrose逆矩阵,利用系统状态、外界干扰、执行机构故障的估计值,设计容错抗干扰控制器,具体形式如下:
[0088][0089]
其中,k是状态反馈增益矩阵,分别代表外界干扰补偿项和执行机构故障补偿项。
[0090]
步骤四:将设计的控制器代入航天器姿态动力学模型,构建闭环姿态控制系统方程,具体形式如下:
[0091]
定义观测误差具有如下形式:
[0092][0093]
记总扰动扩展状态可得到闭环系统状态方程
[0094][0095]
其中,
[0096][0097]
步骤五:设计lyapunov函数,基于线性矩阵不等式理论,推导输入受限情况下闭环系统二次稳定且输出满足鲁棒h
∞
性能约束的充分条件。
[0098]
对于实际在轨运行的航天器,其执行机构存在饱和上限,对于任意轴向的控制力矩应存在以下约束:
[0099]
u
i
(t)=sign(u
i
(t))min{|u
i
(t)|,u
i max
}(i=x,y,z)
[0100]
其中,u
i max
为控制力矩的幅值。
[0101]
设计lyapunov函数:
[0102][0103]
对于给定p0>0,τ
i
>0(i=1,2),κ
s
>0(s=1,2),k0>0,假设存在对称正定矩阵p1,p2,p3,p4和正常数γ,若闭环系统在步骤三所述的控制器作用下具有步骤五所述的二次稳定性并且输出满足鲁棒h
∞
性能约束,则在输入受限情况下,矩阵k和h可以通过求解以下线性矩阵不等式组得到:
[0104]
p0(a
‑
b1k)+(a
‑
b1k)
t
p0<0
[0105][0106][0107][0108]
其中
[0109][0110][0111][0112][0113][0114][0115][0116][0117]
h=p2l
[0118][0119]
由矩阵p2和h,可以得到观测器增益矩阵
[0120]
步骤六:利用matlab工具箱进行线性矩阵不等式的求解,代入闭环控制系统,实现对于外界干扰和故障信号的实时估计,使系统达到稳定状态:
[0121]
系统初始状态x(0)=[0.1rad
ꢀ‑
0.1rad
ꢀ‑
0.08rad
ꢀ‑
0.05rad/s 0.06rad/s 0.08rad/s]
t
;
[0122]
其它参数具有如下形式:
[0123]
τ1=500,τ2=20,k0=0.1,κ3=0.01,κ5=0.01
[0124][0125][0126]
基于上述仿真参数,利用matlab中lmi工具箱求解,可以得到:
[0127]
控制器增益矩阵k:
[0128][0129]
观测器增益矩阵形式如下:
[0130][0131]
在设计的姿态/故障/干扰协同观测与容错抗干扰控制器的作用下,可以得到图2
‑
图6的仿真结果,图2表示航天器姿态角的变化曲线,图3表示航天器姿态角速度的变化曲线,图4表示姿态/故障/干扰协同观测器对执行机构故障信号的观测曲线,图5表示姿态/故障/干扰协同观测器对外界干扰的观测曲线,图6表示在容错抗干扰控制器的作用下航天器姿态稳定过程中控制力矩的变化曲线。结果表明,航天器姿态角、姿态角速度稳定收敛时间大约在15s,稳定状态下姿态角控制精度小于10
‑3rad,姿态角速度控制精度小于10
‑4rad/s,姿态/故障/干扰协同观测器对于外界干扰、执行机构故障信号具有较好的估计效果,控制力矩的幅值不超1nm,满足输入受限条件。
[0132]
基于以上仿真结果可以发现,本发明一种航天器姿态/故障/干扰协同观测与容错抗干扰控制方法能够在外界干扰、测量误差、执行机构故障及饱和受限等复杂情形下,实时地实现对外界干扰、执行机构故障信号的观测,从而实现航天器高精度快速姿态稳定控制。
[0133]
本发明还可有其它多种实施例,在不背离本发明精神及其实质的情况下,本领域技术人员当可根据本发明做出各种相应的改变和变形,但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。
