1.本公开涉及智能交通技术领域，尤其涉及一种多车协同轨迹规划和路径跟踪方法。


背景技术：

[0002]“智能化”、“网联化”是当前汽车行业的发展趋势，也是汽车厂商们竞相追逐的行业热点。在智能网联的环境下，不同车辆之间通过5g和专用短程通信技术(dsrc，dedicated short range communication)等通讯手段进行联系，使得配备了通信设备的车辆可以和周围的甚至在视线外的车辆“交流”，并获取他们的诸如位置、速度、加速度和驾驶意图等信息，这不仅可以提高驾驶的安全性和舒适性，还能减少能源消耗，解决交通拥堵问题。
[0003]
目前的多车变道算法大多都是非合作变道，主车周围的其它车辆不参与变道时的速度调整过程，而在智能网联的环境下，合作变道具有更好的效果。此时，混杂交通流下的单车轨迹规划问题就转化成一个多车协同轨迹规划的问题，如何实现多车协同轨迹规划则是本技术需要解决的问题。


技术实现要素：

[0004]
本公开提供了一种多车协同轨迹规划和路径跟踪方法，其技术目的是在智能网联的环境下，通过多车协作而实现合作变道。
[0005]
本公开的上述技术目的是通过以下技术方案得以实现的：
[0006]
一种多车协同轨迹规划和路径跟踪方法，包括：
[0007]
主车对当前车道和相邻车道进行检测，判断当前车道和相邻车道是否有障碍物，包括：
[0008]
s1：当当前车道不存在障碍物时，根据主车速度及与目标路径的横向偏差计算前轮转向角δf，根据所述前轮转向角δf继续在当前车道行驶，继续跟踪初始目标轨迹；
[0009]
s2：当当前车道存在障碍物且相邻车道没有障碍物时，对当前路径进行重规划，获取重规划轨迹与初始目标轨迹的横向距离e
des
，根据所述横向距离e
des
进行变道；
[0010]
s3：当当前车道存在障碍物且相邻车道也存在障碍物时，将变道过程划分为调整阶段和变道阶段，包括：
[0011]
s31：在所述调整阶段，通过不同加速度获取车辆调整后的不同全局纵向位置，选取最优加/减速度进行调整；
[0012]
s32：在所述变道阶段，根据所述步骤s1或步骤s2进行变道。
[0013]
本公开的有益效果在于：本技术所述的多车协同轨迹规划和路径跟踪方法，将车-车之间的协同变道分解为车速调整和变道汇入两个过程，在调整阶段综合考虑了车辆行驶的安全性、舒适性、交通效率等因素，获取每辆车最优的加/减速度并进行纵向车速调整。该方法能够实现智能网联汽车协同实时轨迹重规划和全局路径跟踪，具有很强的实用性，以及广阔的商业应用前景。
附图说明
[0014]
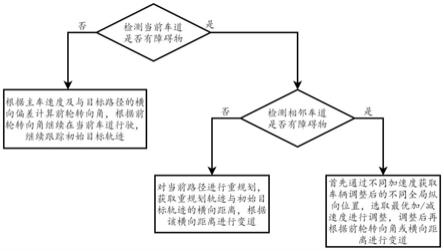
图1为本技术所述方法的流程图；
[0015]
图2为本技术设计的纯跟踪算法原理图；
[0016]
图3为本技术设计的不同加速度带来的交通效率收益示意图；
[0017]
图4为本技术设计的不同加速度带来的舒适性收益示意图；
[0018]
图5为本技术得出的两车同位置同速前进时仿真路径图；
[0019]
图6为本技术得出的两车同位置同速前进时仿真速度图。
具体实施方式
[0020]
下面将结合附图对本公开技术方案进行详细说明。
[0021]
图1为本技术所述方法的流程图，如图1所示，在进行轨迹规划和路径跟踪时，首先主车要对当前车道和相邻车道进行检测，判断当前车道和相邻车道是否有障碍物，包括：
[0022]
s1：当当前车道不存在障碍物时，根据主车速度及与目标路径的横向偏差计算前轮转向角δf，根据所述前轮转向角δf继续在当前车道行驶，继续跟踪初始目标轨迹，包括：
[0023][0024]
其中，l表示前视距离，l表示主车的轴距，θ表示前视方向与主车航向角的夹角，l的选取包括：
[0025][0026]
其中，v
x
表示主车纵向速度，ey表示与目标路径的横向偏差，l
adapt
表示考虑了速度和横向误差影响的自适应前视距离，l
min
表示预设的最小前视距离，kv表示速度系数，ke表示横向偏差系数，且kv为正数，ke为负数。
[0027]
具体地，在进行全局路径跟踪时，采用实时性比较强的纯跟踪算法，如图2所示，给定参考路径，参考路径是一个个全局坐标点，选择一个合适的前视距离l，根据l在目标路径上选择一个跟踪点，通过主车的位姿状态和与目标路径的几何关系规划一端过渡圆弧用以到达跟踪点，使用该过渡圆弧的半径推导出所需的前轮转向角δf。几何关系包括：(16)；式(11)中θ是前视方向与车辆航向角的夹角，即航向偏差；r表示过渡圆弧的半径(即转弯半径)。
[0028]
由式(11)可以计算到达跟踪点的过渡圆弧的曲率λ为：
[0029]
当车辆的轴距l远小于转弯半径r，且车辆质心侧偏角β很小时，根据阿克曼转向几何关系，可以近似得到：
[0030]
根据式(18)可以计算出前轮转向角δf：
[0031]
不同的前视距离会得到不同曲率的过渡圆弧，对前轮转向角有很大影响。过小的前视距离会导致车辆沿跟踪曲线的过度震荡，过大的前视距离会极大程度地降低跟踪的性能，因此，为了改善跟踪效果，本技术考虑了车辆速度和横向偏差对纯跟踪效果的影响，对已有的纯跟踪算法进行改进。在较低的速度时设定一个最小前视距离l
min
，考虑到速度较大时车辆更期望于采取较大的前视距离以跟踪更远处的路径，而横向误差较大时车辆则会更偏向于跟踪较近处的路径点来先减小横向误差，因此采用速度系数kv和横向偏差系数ke来调节总前视距离，且设置kv为正数，ke为负数。前视距离的选取如式(2)所示，最终选取的用于计算前轮转向角的前视距离则是自适应前视距离与最小前视距离中较大的值，防止车速过小且横向偏差过大时车辆的前视距离过小造成跟踪轨迹的严重振荡。
[0032]
步骤s2：当当前车道存在障碍物且相邻车道没有车辆通过时，对当前路径进行重规划，获取重规划轨迹与初始目标轨迹的横向距离e
des
，根据所述横向距离e
des
进行变道，
[0033]
包括：e
des
(σ)＝c0+c1σ+c2σ2+c3σ3；
ꢀꢀꢀ
(3)；
[0034]
其中，σ表示相对变道起始点的纵向位移，c0,c1,c2,c3表示控制系数。
[0035]
考虑到主车重规划轨迹在变道初始位置处应与初始目标轨迹相切，即横向偏差和初始航向角为0，而主车变道的目标为无障碍物车相邻车道的中心线，变道后主车的横向位置即为当前车道到目标车道的宽度w
lane
，整个变道的纵向距离为x
avo
，变道后航向角与初始航向角相同，均为0，可以得到式(4)至式(7)，联合式(4)至式(7)即可得到控制系数c0,c1,c2,c3，包括：
[0036]edes
(0)＝c0＝0；
ꢀꢀꢀ
(4)；
[0037][0038]edes
(x
avo
)＝c0+c1x
avo
+c2x
avo2
+c3x
avo3
＝w
lane
；
ꢀꢀꢀ
(6)；
[0039][0040]
式(4)至式(7)这四个线性独立的方程可以解出四个控制系数，由此可以确定重规划轨迹上任意点的横向位置e
des
，只需要取原始直线路径上的点进行该横向距离值的偏移使用偏移后的点作为预瞄点，并随着车辆行驶将偏移值逐渐增大到w
lane
后保持该偏移值，即可完成变道轨迹的跟踪并且沿变道后的车道行驶。
[0041]
在进行横向换道轨迹规划时，不仅要考虑行驶安全性，还需要考虑驾驶员和乘客对于障碍物的个性化主观风险感受，这是影响无人驾驶车辆中驾驶员舒适性的重要因素。主车换道轨迹由两个参数决定，w
lane
和x
avo
，w
lane
表示当前车道到目标车道的宽度，与目标安全车道的选择有关。x
avo
表示整个变道的纵向距离，即主车避障距离，由主车纵向车速v
x
和驾驶员期望的换道时间t
lc
决定，x
avo
＝v
x
*t
lc
。本技术通过选择合适的避障时间t
lc
，来规划出符合驾驶员个性化主观感受的避障轨迹，则有
[0042]
其中，t0为中性驾驶员在当前车速下的避障时间，p∈[-1,1]为驾驶员风格系数。p越大，驾驶员的激进性越强，主车的避障距离越短，避障效率越高；p越小则驾驶员越保守，避障距离越长。
[0043]
s3：当当前车道存在障碍物且相邻车道也存在移动车辆时，将变道过程划分为调整阶段和变道阶段，包括：
[0044]
s31：在所述调整阶段，通过不同加速度获取车辆调整后的不同全局纵向位置，选取最优加/减速度进行调整，包括：
[0045][0046][0047][0048][0049]
其中，a表示在当前车道的主车，b表示在相邻车道的车辆；和分别表示主车a和车辆b的相对调整距离；和分别表示主车a和车辆b在所述调整阶段结束后的全局纵向位置；表示主车a的初始速度，表示车辆b的初始速度；t
ad
表示主车a及车辆b的每次加/减速的调整时间；aa和ab分别表示主车a和车辆b的加速度。
[0050]
具体地，调整阶段两车进行纵向速度的合作调整，例如定义右车道的车辆为a车(即当前车道的主车)，左车道的车辆为b车(即相邻车道的车辆)，a车在平直车道上行驶时，通过激光雷达检测到前方的障碍物，激光雷达检测a车与障碍物的有效距离为d
det
，在障碍物进入a车激光雷达的检测区域后，a车和b车进行通信来协同变道。
[0051]
首先要进行纵向的车速调整，将纵向调整阶段分为两个部分，左右车道的两辆车先进行一次加/减速拉开距离，再进行一次加/减速调整继续保持原始车速，假设两次调整时间均为t
ad
，a、b两车在全局坐标系下的初始纵向位置分别为初始速度分别为为了保证调整过程有较好的舒适性，本技术在调整过程中采用恒定的加速度，使得调整时的急动度为0。
[0052]
假设第一次调整的加速度为aa、ab，由于调整时间相同，为了让调整后的车辆速度能回到原始车速，第二次调整的加速度为-aa、-ab，假设车辆的最大加速度为a
max
，a、b两车均在区间[-a
max
,a
max
]之间选取一个加速度形成一个加速度组合用以进行纵向速度调整，可以得到不同的调整结果，即式(8)至式(9)。
[0053]
和分别为a车和b车的相对调整距离，即采用加减速调整后相比于使用原始车速行驶多出的调整距离，第一次调整车辆加速则该调整距离为正，反之则为负，和为a、b两车整个调整阶段结束后的全局纵向位置。在得到不同加速度获取的不同调整位置后，就可以在其中选取一组最优的加速度进行调整。
[0054]
进一步地，在步骤s31中，可以根据交通效率、舒适性和驾驶员风格系数建立多目标收益函数，再根据所述全局纵向位置和所述多目标收益函数选取最优加/减速度，包括：
[0055]
[0056][0057]
c＝w
gcg
+waca+w
pcp
；
ꢀꢀꢀ
(14)；
[0058]
其中，g表示调整后主车a和车辆b的距离，la表示主车a的长度，lb表示车辆b的长度，ds表示车辆在调整后与后车保持的安全距离；d
det
表示传感器的有效检测距离，c表示总收益，cg表示调整后两车距离g所带来的交通效率项收益值，ca表示舒适性收益函数，c
p
表示驾驶员风格收益函数；wg、wa、w
p
分别表示交通效率收益项、舒适性收益项和驾驶员风格收益项的权重系数。
[0059]
具体地，本技术综合考虑安全性、舒适性、交通效率以及驾驶员激进特性等几个方面对加速度组合进行评估，来衡量加速度组合的优异程度。首先是要保证安全性，为了确保车辆在变道过程以及之后行驶过程的安全性，车辆在调整后需要与后车保持一定的安全距离ds，后车的速度越高则安全距离越大，如下式所示：
[0060][0061]
其中，vr为调整后选择跟车车辆的速度，为车辆紧急制动时的最大加速度。式(19)保证了车辆在前车突然故障的情况下后车能够紧急制动防止意外的发生。若调整后两车之间的距离为g，则可得到式(12)。
[0062]
根据式(12)，为了保证a车有足够的距离进行变道，需要计算a车的最大调整距离，由上一步可以得到a车的避障距离为x
avo
，可以计算出预留的调整距离如式(13)。
[0063]
然而，除了需要保证安全性以外，为了提升交通效率，g并非越大越好，车辆之间过大的空间会导致道路利用效率低，因此只需要调整到两车间距大于安全距离而又不会过大的程度。本技术设计了一个正态分布的收益函数来评估拉开的距离g能够提升的交通效率。
[0064][0065]
其中，cg为调整后两车距离所带来的交通效率项收益值，σ1可以调整收益曲线下降的速率。
[0066]
当σ1＝6时的收益如图3所示。拉开距离在9m左右时，能够大幅提升道路的利用率，因此能够获得较高的收益，拉开的距离越大，获得的收益就越低，在拉开30m距离时，此时两车之间还能插入其它车辆，道路利用率低，收益几乎为0。
[0067]
其次，考虑调整时车辆的乘坐舒适性，两车分别在区间[-a
max
,a
max
]之间选取一个加速度进行纵向速度调整，选取的加速度越小越能够得到舒适的驾驶体验，此时舒适性收益函数项ca为：
[0068]
[0069][0070]
其中，a
rms
为两车两次加速度的均方根值，为a、b两车进行两次加减速时的加速度。σa＝0.7时的收益图像如图4所示，当整体的加速度均方根值越接近于0，获得的舒适性收益越高。
[0071]
然后，在纵向速度调整阶段，本技术创新性的引入了两车驾驶员的个性化激进性驾驶风格，与上一节轨迹规划的驾驶风格设定相同，设a、b车两个驾驶员的风格系数分别为其中驾驶员风格系数越接近1，则驾驶员越激进，越接近-1，则驾驶员越保守，激进的驾驶员往往会在调整的时候尽可能地选择超车调整，而保守驾驶员则更可能进行跟车调整。基于此，本技术设置一个驾驶员风格收益函数c
p
来评估两车车速调整的方式与驾驶员偏好的符合程度。
[0072][0073]
该收益为两辆车的驾驶员风格系数与对应车辆的相对调整距离的乘积之和，当驾驶员的驾驶风格为激进时，驾驶风格系数为正数，相对调整距离越大则收益越高，代表驾驶员更愿意在原来的速度上进行加速调整再回到原始车速，从而达到超车的期望。反之，驾驶员风格系数为负数时，若车辆加速而导致相对调整距离为正值，得到的收益为负值，即该加减速会导致收益减小，不符合驾驶员预期。该收益项作为两车的收益之和，在加减速都符合两个驾驶员的驾驶风格时能够得到最大的收益，若是都不符合驾驶员的驾驶风格，则收益为负，导致最后的总收益会被大幅减小，若是仅符合其中一个驾驶员的驾驶偏好，则收益较为一般。
[0074]
最后，在确保了安全性的前提下，综合考虑了交通效率、舒适性以及驾驶员驾驶风格的总收益函数c如式(14)所示。
[0075]
通过上述方法，在[-a
max
,a
max
]之间寻找到一个合适的a车与b车调整加速度组合，使得总收益c最大。通过该加速度组合进行纵向速度调整，即可拉开合适的距离，保证变道过程后两车行驶的安全性。
[0076]
在步骤s32中的变道阶段，则继续根据所述步骤s1或步骤s2进行变道。
[0077]
作为具体实施例地，为了验证本技术所述方法的有效性，本技术对比了a、b两车同位置同速时a车检测到障碍物要进行变道避障的情况下，两车驾驶员个性化驾驶风格变化带来的影响。a、b两车初始车速均为40km/h，a车辆在第二秒时检测到障碍物开始与b车辆进行协同调整后变道汇入。
[0078]
当t
ad
＝2s，a
max
＝2.5m/s2，，σ1＝10，σa＝0.8，d
det
＝100m，wg＝0.5,wa＝1,w
p
＝0.1，对于不同的驾驶员风格系数进行研究。
[0079]
若pa＝0.5，pb＝-0.5，此时算法仿真结果如图5中(a)和图6中(a)所示，其中图5中(a)相同的图形为两辆车在同一时刻的位置，每经过2s用一种形状来代表车辆在该时刻的位置。可以看到，a车驾驶员激进，b车驾驶员保守的情况下，两辆车为了拉开安全距离，a车加速，b车减速，这样得到的驾驶员收益项值最大，从图6中(a)来看，a、b两车恰好使用了相反的加减速度进行加减速，这是二者驾驶风格相反、初始位置与初始速度相同导致的。
[0080]
若pa＝-0.5，pb＝0.5，此时算法仿真结果如图5中(b)和图6中(b)所示，两车加减速情况恰好与上一组仿真度加减速情况相反，此时a车保守，b车激进，而仿真情况为a车减速，b车加速，充分说明了驾驶员驾驶风格在其中起到的影响。
[0081]
若pa＝0.6，pb＝0.5，该驾驶员系数下的算法仿真结果如图5中(c)和图6中(c)所示，若两个驾驶员均为激进的驾驶风格，在预留的避障距离足够的情况下，算法会满足驾驶风格更加激进的车辆，即保证驾驶员收益项为正值。从图6中(c)可以看出，a车与b车的加减速度不是互为相反数，这是因为b车驾驶员收益项为负值，为了保证总驾驶员收益较高，b车采取了较小的加减速度组合，同时a车为了拉开安全距离，仍使用与图6中(a)相同的加减速度来减速，也获得了较高的驾驶员收益值。
[0082]
本领域的技术人员应该了解,本技术不受上述实例的限制,上述实例和说明书中描述的只是说明本发明的原理,在不脱离本发明精神和范围的前提下本发明还会有各种变化和改进,这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等同物界定。