1.本发明涉及一种自动驾驶汽车换道决策规划方法，特别涉及一种考虑路面附着系数的自动驾驶汽车类人换道决策规划方法。


背景技术：

2.自动驾驶汽车(autonomous vehicles，av)是一项高速发展且日益成熟的技术，有可能通过提高汽车运输的安全性、可达性、效率和便利性来重塑移动出行概念，是世界汽车工业发展的必然趋势和主要赛场，也是我国汽车工业的战略制高点。自动驾驶车辆必须能够执行的安全关键任务包括在与其他车辆和行人共享的动态环境下进行合理运动规划，以及控制的鲁棒性。在现阶段，对单车来说，人类驾驶员和自动驾驶汽车共同完成驾驶任务的情况将共存；从多车角度来说，自动驾驶汽车与人类驾驶汽车共同构成混合交通局面。在未来，鉴于人类对驾驶活动的热情与对极致驾驶感受的追求，即使在高等级自动驾驶汽车普及的时代，人类驾驶汽车的情况也不会消失，故可以推断人机共驾和混合交通的情景将长期存在。人类具有出色的场景泛化，技能学习，紧急情况处理能力；因此研究人类驾驶员的驾驶行为与驾驶习性机理，并使自动驾驶汽车理解人类驾驶方式、像人类一样进行驾驶，提升人对av的乘坐认同感，是智能驾驶汽车研究中不可忽视的方面。
3.在自动驾驶汽车技术体系中，决策规划是系统的中枢，承接感知与控制层，是提高车辆智能性、安全性、经济性、舒适性以及用户接受度和交通协调度的关键，因此，决策规划问题一直是自动驾驶汽车研究领域的热点和难点。当前自动驾驶汽车自主决策规划研究大多采用基于规则或基于学习的方法。随着人工智能技术的不断进步，基于数据学习的自动驾驶汽车决策规划策略引起了越来越多的关注，常用的学习算法有决策树、概率图模型、深度学习、强化学习等，但现有的换道决策规划方法缺少考虑实时的路面附着系数对于决策规划的影响，学习类方法存在泛化性较差、机理不明晰等问题。


技术实现要素：

4.为了解决上述技术问题，本发明提供一种考虑路面附着系数的自动驾驶汽车类人换道决策规划方法，包括以下步骤：
5.步骤一、分别采集良好路面附着系数、中等路面附着系数和低路面附着系数下的熟练驾驶人换道数据；
6.步骤二、对所采集的换道数据进行预处理，以及统计学特征计算、特征构造，对良好路面附着下采集到的数据特征序列与特征值进行anova相关性分析，得到对驾驶人换道行为具有显著影响的特征序列和特征值，后引入不同附着系数μ下采集得到的驾驶数据，分析μ是如何影响驾驶人的换道行为，得出映射关系；分析结果表明，当路面附着系数μ降低时相比于正常附着情况：
7.1、换道切入点远离前车；
8.2、换道过程自车侧向加速度峰值a
ymax
降低；
9.3、换道时长增加；
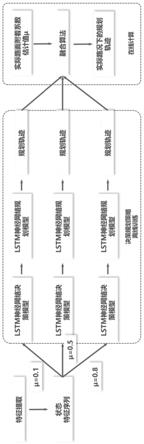
10.步骤三、将三种常见附着系数μ＝0.1、0.5、0.8下的驾驶人换道数据分别送入三个基于lstm的神经网络决策规划模型，神经网络决策规划模型采用分层架构，先使用神经网络决策模型深度学习的方法学习人类换道决策行为，即左换道、右换道、保持跟车三种决策；再使用神经网络规划模型深度学习的方法学习人类换道轨迹，得到当前交通环境下每种附着下的预测轨迹输出，即μ＝0.1、0.5、0.8下的三条轨迹；
11.步骤四、在驾驶任务中，决策规划系统实时接收由感知系统识别得到的实际路面附着系数的估计值结合离散附着系数的输出轨迹，采用拉格朗日三次多项式插值法进行轨迹融合：
[0012][0013]
其中，x0、y0，x1、y1，x2、y2分别为μ＝0.1、0.5、0.8下的轨迹坐标，x、y为融合后的轨迹坐标值；
[0014]
最终得到当前实际路况下的实时决策行为以及规划轨迹，并将规划轨迹传递给控制层作为跟踪轨迹。
[0015]
进一步的，步骤一中，搭建基于vi-grade软硬件平台的高精度高拟真驾驶模拟器数据采集平台进行驾驶人换道数据的采集；
[0016]
软件环境中，采用vi-worldsim作为场景软件，使用unreal虚幻4渲染引擎，对车辆、车道、天气、路线等进行配置，视觉场景效果更加逼真；建立不同天气条件下的换道场景，并使附着系数产生对应的变化；采用vi-simsound声学模块，提供nvh仿真级声效，提升声觉感受；首先建立用于数据采集及验证的高精度车辆动力学模型，对整车七个子系统包括转向、悬架、制动、转向、动力系统、轮胎、空气动力学系统分别建模，由于静态即使模拟器的反馈主要来自于转向系统反馈，故车辆转向建模用pfeffer的高级物理转向模型，详细描述了转向系统各运动副的摩擦和阻尼力，确保力反馈的真实，包括：
[0017]
(1)指数弹簧摩擦(esf)模型：
[0018][0019]
其中，f
sf
为摩擦力，f
lim
是摩擦力极限值，f
esf
为x为0时的刚度，如图6所示。
[0020][0021]
(2)指数弹簧摩擦模型结合平行麦克斯韦模型(esfm)：
[0022]
esfm单元采用并行非线性麦克斯韦模型进行增强，以覆盖动态效应；
[0023]fm
＝f
m,lim
·
tanh(km·
v)
[0024]
其中，fm为麦克斯韦摩擦力，f
m，lim
为最大的弹簧力，km为弹簧刚度，如图7所示。
[0025]
(3)伪库仑摩擦模型：为了将依赖于载荷的摩擦效应考虑到模型中(平移或旋转)，可选用一个伪库仑类型的摩擦模型，根据方程摩擦力或力矩与施加的载荷有线性依赖关系：
[0026][0027]
其中，fc为伪库伦摩擦力，fn是元素负载，vs为元素相对速度；vt是静摩擦与动摩擦之间的过渡速度，如图8所示。
[0028]
然后在仿真软件中建立与实车道路试验相同的工况并进行仿真，通过与客观试验采集数据对标，确保该模型稳态和瞬态响应精度高达90％以上；
[0029]
硬件部分的转向电机采用fanatecdd2直驱电机基座，其峰值扭矩达20n
·
m，具备1:1复现转向系统力反馈的能力；制动踏板总成采用fanatecv3踏板，方向盘盘体使用原车方向盘保证触感与原车一致，解算模块采用具有6个cpu核心的concurrent实时仿真机，保证解算实时性，场景渲染采用搭载rtx3090的工作站保证画面流畅度。
[0030]
进一步的，步骤一中所采集的换道数据包括：换道和超车过程中本车道前车车距df、本车道前车相对速度vf、本车道后车车距dr、本车道后车相对速度vr、换道时长tc、换道距离sc、换道过程自车侧向加速度峰值a
ymax
、换道过程自车侧向加速度均值a
yave
、换道过程自车纵向加速度峰值a
xmax
、换道过程自车纵向加速度均值a
xave
、预计碰撞时间t
ttc
。
[0031]
进一步的，步骤二中具体包括以下步骤：
[0032]
第一步：标准差标准化(z-score)：
[0033]
z-score标准差标准化为类似正态分布，均值为0，标准差为1：
[0034]
其中均值为标准差为
[0035]
第二步：对于所属范围未知或者所属范围是全体实数，同时不服从正态分布的数据进行非线性归一化：
[0036]
tanh函数：
[0037]
第三步：相似性度量，采用dtw对不同长度的数据进行比较分析，通过降低其时间和空间复杂度探究其内在特征：
[0038]
设定向量c＝{c(1),c(1),...,c(n)}，其中，c(n)＝(i(n),j(n))，i,j为两个不同长度的序列，c(n)即为第n个匹配点对，d(x
i(n)
,y
j(n)
)为两个点的局部匹配距离；dtw即通过优化时间规整目标函数实现不同长度序列匹配点加权距离总和最小：
[0039][0040]
定义最小累计匹配函数g(i,j)，表示所有匹配点对的最小累计匹配距离：
[0041][0042]
在计算的时候，首先令i(1)＝j(1)＝1,g(1,1)＝2d(x1,y1)
[0043][0044]
其中，reg为平行四边形约束区域，两条边的斜率为0.5和2，同时两个顶点坐标分别为(1，1)和(i,j)；通过递推求解g(i,j)来确定下一匹配点：
[0045][0046]
其中，i＝2,3,
…
,i；j＝2,3,
…
,j；(i,j)∈reg；
[0047]
第四步：对良好附着下采集到的数据特征序列与特征值进行anova相关性分析，得到对驾驶人换道行为具有显著影响的特征序列和特征值，后引入不同附着系数μ下采集得到的驾驶数据，分析μ是如何影响驾驶人的换道行为，得出映射关系。
[0048]
进一步的，步骤三中所述的基于lstm的神经网络决策规划模型输入向量定义为所提取的特征序列i、两个换道标志位m以及道路曲率ρ，输出即为自车在预测时域内的横纵向坐标序列以及速度序列，记为o；
[0049]
网络框架如下，输入经过relu函数激活的全连接层处理后进入lstm单元，lstm共包含遗忘门(forget gate)f
t
、输入门(inputgate)i
t
、输出门(outputgate)o
t
和一个类似于隐含层的细胞状态(cell state)c
t
；其中，遗忘门以上一时刻的隐含层状态h
t-1
和当前时刻的输入量x
t
作为输入，以对上一时刻的细胞状态c
t-1
保留比例作为输出：
[0050]ft
＝σ(w
fx
x
t
+w
fhht-1
+bf)
······················
(3.1)
[0051]
下一步即确定在细胞状态中保留哪些新信息，主要分为两部分，一部分是通过输入门确定哪些值需要进行更新：
[0052]it
＝σ(w
ix
x
t
+w
ihht-1
+bi)
······················
(3.2)
[0053]
另一部分是通过一个tanh网络层来创建一个细胞状态更新部，用来添加到细胞状态；这两部分点乘运算的结果即为当前输入对网络状态的更新：
[0054][0055][0056]
最后，通过输出门和更新后的细胞状态确定当前时刻隐含层的输出：
[0057]ot
＝σ(w
ox x
t
+w
oh h
t-1
+bo)
·····················
(3.5)
[0058]ht
＝o
t
⊙
tanh(c
t
)
························
(3.6)
[0059]
式中，
⊙
为哈达玛积(hadamard product)，w
fx
、w
fh
、w
ix
、w
ih
、w
cx
、w
ch
、w
ox
、w
oh
为网络的权重矩阵，bf、bi、bc、bo为网络的偏置向量，tanh(
·
)和σ(
·
)分别是双曲正切函数和sigmoid函数：
[0060][0061][0062]
通过这种方式学习历史轨迹序列中的规律，经softmax函数归一后输出换道意图
概率向量ω再经过one-hot编码后生成最终换道决策，换道概率超过80％的决策转化为100％；
[0063]
同时，一个lstm负责将被预测车辆的历史轨迹信息及其周围车辆的历史轨迹信息编码为一个固定长度的上下文向量r，该向量包含了编码器对历史轨迹特征的理解与记忆；
[0064]
再经过一个lstm网络后得到预测时域的输出轨迹。
[0065]
本发明的有益效果：
[0066]
本发明相比以往采用的驾驶模拟器作为数采工具的研究，模型和硬件可信度更高，采集轨迹更真实，本发明在充分发挥模拟器的场景一致性、安全性、经济性的同时，提升驾驶模拟器的沉浸感、真实感，确保采集数据的客观性、真实性，是领域内首次实现。
[0067]
外界复杂动态场景的不确定性(以μ的变化为例)、环境驾驶人驾驶行为的多变性对换道行为的影响复杂，往往采用学习类方法解决；但学习类方法存在泛化性较差、机理不明晰等问题。本发明结合数据驱动和机理分析，实现优势互补。
[0068]
人类具有出色的场景泛化，技能学习，紧急情况处理能力，本发明研究人类驾驶员的驾驶行为与驾驶习性机理，并使自动驾驶汽车理解人类驾驶方式、像人类一样进行驾驶，提升人对自动驾驶汽车的乘坐认同感，为提升智能驾驶汽车接受度提供了方法。
附图说明
[0069]
图1为本发明整体流程示意图；
[0070]
图2为本发明驾驶模拟器数据采集平台的结构示意图；
[0071]
图3为本发明基于lstm的神经网络决策规划模型结构示意图；
[0072]
图4为本发明换道过程示意图；
[0073]
图5为本发明换道过程中横摆角随时间变化示意图；
[0074]
图6为本发明指数弹簧摩擦(esf)模型示意图；
[0075]
图7为本发明指数弹簧摩擦模型结合平行麦克斯韦模型(esfm)模型示意图；
[0076]
图8为本发明伪库伦摩擦模型示意图。
具体实施方式
[0077]
请参阅图1-8所示：
[0078]
本发明提供一种考虑路面附着系数的自动驾驶汽车类人换道决策规划方法，包括以下步骤：
[0079]
步骤一、搭建基于vi-grade软硬件平台的高精度高拟真驾驶模拟器数据采集平台进行驾驶人换道数据的采集；
[0080]
软件环境中，采用vi-worldsim作为场景软件，使用unreal虚幻4渲染引擎，对车辆、车道、天气、路线等进行配置，视觉场景效果更加逼真；建立不同天气条件下的换道场景，并使附着系数产生对应的变化；采用vi-simsound声学模块，提供nvh仿真级声效，提升声觉感受；建立用于数据采集及验证的高精度车辆动力学模型，对整车七个子系统(转向、悬架、制动、转向、动力系统、轮胎、空气动力学系统)分别建模，车辆转向建模应用pfeffer的高级物理转向模型，详细描述了转向系统各运动副的摩擦和阻尼力，包括：
[0081]
(1)指数弹簧摩擦(esf)模型：
[0082][0083]
其中，f
sf
为摩擦力，f
lim
是摩擦力极限值，f
esf
为x为0时的刚度，如图6所示。
[0084]
(2)指数弹簧摩擦模型结合平行麦克斯韦模型(esfm)：
[0085]
esfm单元采用并行非线性麦克斯韦模型进行增强，以覆盖动态效应；
[0086]fm
＝f
m,lim
·
tanh(km·
v)
[0087]
其中，fm为麦克斯韦摩擦力，f
m，lim
为最大的弹簧力，km为弹簧刚度，如图7所示。
[0088]
(3)伪库仑摩擦模型：为了将依赖于载荷的摩擦效应考虑到模型中(平移或旋转)，可选用一个伪库仑类型的摩擦模型，根据方程摩擦力或力矩与施加的载荷有线性依赖关系：
[0089][0090]
其中，fc为伪库伦摩擦力，fn是元素负载，vs为元素相对速度；vt是静摩擦与动摩擦之间的过渡速度，如图8所示。
[0091]
然后在仿真软件中建立与实车道路试验相同的工况并进行仿真，通过与客观试验采集数据对标，确保该模型稳态和瞬态响应精度高达90％以上；
[0092]
硬件部分的转向电机采用fanatecdd2直驱电机基座，其峰值扭矩达20n
·
m，具备1:1复现转向系统力反馈的能力；制动踏板总成采用fanatecv3踏板，方向盘盘体使用红旗原车方向盘保证触感与原车一致，解算模块采用具有6个cpu核心的concurrent实时仿真机，保证解算实时性，场景渲染采用搭载rtx3090的工作站保证画面流畅度。
[0093]
高精度高拟真驾驶模拟器数据采集平台搭建完成后，招募熟练驾驶员，首先进行至少30分钟的正常路面附着系数下的驾驶练习，随后开始实验，实验设计如下表：
[0094]
表1实验设计表
[0095][0096]
依照上述实验设计分别采集路面附着系数μ＝0.8、0.5、0.1下的熟练驾驶人换道数据；所采集的换道数据包括：在表1工况类别下的换道和超车过程中的本车道前车车距df
、本车道前车相对速度vf、本车道后车车距dr、本车道后车相对速度vr、换道时长tc、换道距离sc、换道过程自车侧向加速度峰值a
ymax
、换道过程自车侧向加速度均值a
yave
、换道过程自车纵向加速度峰值a
xmax
、换道过程自车纵向加速度均值a
xave
、预计碰撞时间t
ttc
。
[0097]
步骤二、对所采集的换道数据进行数据清洗、数据变换等预处理，以及统计学特征计算、特征构造，得到特征序列与特征值的集合：
[0098]
第一步：标准差标准化(z-score)：
[0099]
z-score标准化(标准差标准化)为类似正态分布，均值为0，标准差为1：
[0100]
其中均值为标准差为
[0101]
第二步：对于所属范围未知或者所属范围是全体实数，同时不服从正态分布的数据进行非线性归一化：
[0102]
tanh函数：
[0103]
第三步：相似性度量，采用dtw对不同长度的数据进行比较分析，通过降低其时间和空间复杂度探究其内在特征：
[0104]
设定向量c＝{c(1),c(1),...,c(n)}，其中，c(n)＝(i(n),j(n))，i,j为两个不同长度的序列，c(n)即为第n个匹配点对，d(x
i(n)
,y
j(n)
)为两个点的局部匹配距离；dtw即通过优化时间规整目标函数实现不同长度序列匹配点加权距离总和最小：
[0105][0106]
定义最小累计匹配函数g(i,j)，表示所有匹配点对的最小累计匹配距离：
[0107][0108]
在计算的时候，首先令i(1)＝j(1)＝1,g(1,1)＝2d(x1,y1)
[0109][0110]
其中，reg为平行四边形约束区域，两条边的斜率为0.5和2，同时两个顶点坐标分别为(1，1)和(i,j)；通过递推求解g(i,j)来确定下一匹配点：
[0111][0112]
其中，i＝2,3,
…
,i；j＝2,3,
…
,j；(i,j)∈reg；
[0113]
第四步：对良好附着下采集到的数据特征序列与特征值进行anova相关性分析，得到对驾驶人换道行为具有显著影响的特征序列和特征值，后引入不同附着系数μ下采集得到的驾驶数据，分析μ是如何影响驾驶人的换道行为，得出映射关系如下表所示：
[0114]
表2采集特征及映射关系列表
[0115][0116]
分析结果表明，当路面附着系数μ降低时相比于正常附着情况：
[0117]
1、换道切入点远离前车；
[0118]
2、换道过程自车侧向加速度峰值a
ymax
降低；
[0119]
3、换道时长增加；
[0120]
步骤三、将三种常见附着系数μ＝0.1、0.5、0.8下的驾驶人换道数据分别送入三个基于lstm的神经网络决策规划模型，神经网络决策规划模型采用分层架构，先使用神经网络决策模型深度学习的方法学习人类换道决策行为，即左换道、右换道、保持跟车三种决策；再使用神经网络规划模型深度学习的方法学习人类换道轨迹，得到当前交通环境下每种附着下的预测轨迹输出，即μ＝0.1、0.5、0.8下的三条轨迹；
[0121]
所述的基于lstm的神经网络决策规划模型输入向量定义为所提取的特征序列i、两个换道标志位m以及道路曲率ρ，输出即为自车在预测时域内的横纵向坐标序列以及速度序列，记为o；
[0122]
网络框架如下，输入i经过relu函数激活的全连接层处理后进入lstm单元，lstm共包含遗忘门(forget gate)f
t
、输入门(inputgate)i
t
、输出门(outputgate)o
t
和一个类似于隐含层的细胞状态(cell state)c
t
；其中，遗忘门以上一时刻的隐含层状态h
t-1
和当前时刻的输入量x
t
作为输入，以对上一时刻的细胞状态c
t-1
保留比例作为输出：
[0123]ft
＝σ(w
fx
x
t
+w
fhht-1
+bf)
······················
(3.1)
[0124]
下一步即确定在细胞状态中保留哪些新信息，主要分为两部分，一部分是通过输入门确定哪些值需要进行更新：
[0125]it
＝σ(w
ix
x
t
+w
ihht-1
+bi)
······················
(3.2)
[0126]
另一部分是通过一个tanh网络层来创建一个细胞状态更新部，用来添加到细胞状
态；这两部分点乘运算的结果即为当前输入对网络状态的更新：
[0127][0128][0129]
最后，通过输出门和更新后的细胞状态确定当前时刻隐含层的输出：
[0130]ot
＝σ(w
ox x
t
+w
oh h
t-1
+bo)
····················
(3.5)
[0131]ht
＝o
t
⊙
tanh(c
t
)
·······················
(3.6)
[0132]
式中，
⊙
为哈达玛积(hadamard product)，w
fx
、w
fh
、w
ix
、w
ih
、w
cx
、w
ch
、w
ox
、w
oh
为网络的权重矩阵，bf、bi、bc、bo为网络的偏置向量，tanh(
·
)和σ(
·
)分别是双曲正切函数和sigmoid函数：
[0133][0134][0135]
通过这种方式学习历史轨迹序列中的规律，经softmax函数归一后输出换道意图概率向量ω再经过one-hot编码后生成最终换道决策，换道概率超过80％的决策转化为100％；
[0136]
同时，一个lstm负责将被预测车辆的历史轨迹信息及其周围车辆的历史轨迹信息编码为一个固定长度的上下文向量r，该向量包含了编码器对历史轨迹特征的理解与记忆；
[0137]
再经过一个lstm网络后得到预测时域的输出轨迹。
[0138]
步骤四、在驾驶任务中，决策规划系统实时接收由感知系统识别得到的实际路面附着系数的估计值结合离散附着系数的输出轨迹，采用拉格朗日三次多项式插值法进行轨迹融合：
[0139][0140]
最终得到当前实际路况下的实时决策行为以及规划轨迹，并将规划轨迹传递给控制层作为跟踪轨迹，如图4，图5所示。