一种基于min
‑
max单分类深度神经网络的城市噪声识别方法
技术领域
1.本发明属于声音信号识别和深度神经网络领域，涉及一种基于min
‑
max单分类深度神经网络的城市噪声识别方法。


背景技术：

2.随着我国城镇化进程的加快和城市的飞速发展，噪声污染问题日益严重，很大程度上影响了城市的环境和人们的健康，城市噪声问题是当前城市发展面临的环境问题之一。采用人工智能方法，构建全天候智能监测系统，是目前该领域的一个主流方式。目前常见的城市噪声识别方法多是基于传统的语音特征提取算法结合多分类器的方式。然而这些方法存在着以下问题：
3.1)传统的声学特征提取方法无法充分表示复杂的城市噪声；而使用的多分类器受限于其弱表示能力，泛化能力有限。
4.2)目前的大部分研究是基于人工定义好的各种噪声类别。然而各种信号类型无法穷举且具有随机不确定性，这些方法并不适用，且使监测系统面临建模难的问题。
5.3)传统的噪声识别方法是基于一段短时范围内的声信号提取特征，而短时范围内的声信号存在非平稳性，其包含的时空信息有限。
6.因此，目前针对城市噪声的识别监测方法仍有很多改进的空间。


技术实现要素：

7.本发明提出了一种基于min
‑
max单分类深度神经网络的城市噪声识别方法来克服上述城市噪声识别中存在的问题。单分类算法更加贴合城市噪声监测。由于城市噪声种类多种多样且每种类型的声特性存在着差异，采集所有类型噪声信号数据显然是不切实际。因此该方法分别采用以下方式进行改进，包括1)通过对每一种新出现的城市噪声建立单分类深度神经网络模型，获取包围同一类声音数据的超球面，来解决无法穷举各种声音类型的问题；2)构建深度神经网络，提升模型对城市噪声信号的表示能力，提升监测性能；3)构建min
‑
max单分类损失函数，通过对超球面半径隐式地约束，提升模型性能。
8.本发明的技术方案主要包括如下步骤：
9.步骤1、采集城市噪声信号，对采集的噪声信号进行预处理，包括去噪、分帧、加窗(其中帧长和帧移分别设为l和)，最后转换为时频图；得到训练数据集x
n
×
k
＝[x1，
…
，x
n
]，其中n为所有训练样本的数量，k指代每个样本的维度。
[0010]
步骤2、构建深度卷积神经网络，网络构成方法可以采用以下方式：1)以卷积、池化、激活构成卷积块，搭建深度卷积神经网络，并采用卷积自编码器进行网络权重初始化；2)采用在imagenet上预训练的现有深度卷积神经网络结构。
[0011]2‑
1、对于方式1)：深度卷积神经网络由若干卷积块组成，每个卷积块结构一致，包含卷积层、池化层、数据归一化层，卷积块的最后与全连接层相连，网络中激活函数均采用
relu函数。特征x经过卷积层的输出为：
[0012]
y＝w*x+b
ꢀꢀ
(1)
[0013]
其中，w为卷积的权重矩阵，b为其对应的偏置，*代表卷积操作。
[0014]
卷积层的输出进入数据归一化函数的定义：
[0015][0016]
其中，y为卷积层的输出，mean(y)和var(y)分别表示数据的均值和方差，eps为防止分母出现零所增加的变量；γ和β分别为缩放变量和平移变量，加入缩放变量和平移变量的原因是保证每次得到的归一化的值都符合标准正态分布。
[0017]
数据归一化后的结果激活之后接入池化层，其表达式为：
[0018][0019]
y＝f
relu
(σ(y))
ꢀꢀ
(4)
[0020][0021]
其中f为relu激活函数,其中σ为数据归一化函数。z是经过池化层输出后的多维特征，将z展平成一维的向量送入全连接层。
[0022]
最后，采用卷积自编码器，并将卷积自编码器训练好的网络权重，作为构建好的卷积神经网络每个卷积块的初始权重。
[0023]2‑
2、对于方式2)：采用在imagenet上预训练的神经网络作为框架，对预训练网络结构进行调整，删除最后一层全连接层之后的其余层，将最后一层的全连接层输出作为网络输出。
[0024]
步骤3、构建单分类min
‑
max损失函数，训练神经网络权重、单分类超球面球心、以及决策阈值。
[0025]3‑
1.单分类min
‑
max损失函数如下：
[0026][0027]
min
‑
max损失函数通过最小化每个batch中样本到球心最大的距离，通过距离来更新网络权重ω。其中，m是每一个batch中的样本个数，样本总数为n。是将样本x
i
映射到超球面的函数，即上一步骤中构建的网络输出。c是超球面的球心，大小为n*1的向量。
[0028]
对于步骤2的方式1)：使用卷积自编码器对网络进行权重初始化，训练所有样本。c初始值取第一次前向传播后输出结果的均值，计算公式如下：
[0029][0030]
其中α
i
是样本经过网络输出后得到的n*1的向量。
[0031]
对于步骤2的方式2)：将所有样本经过网络的第一次前向传播输出均值作为c初始
值。
[0032]3‑
2.通过adam优化器寻求最优网络权重ω：
[0033]
将训练样本x
n
×
k
＝[x1,
…
x
n
]送入步骤2搭建好的神经网络，采用随机梯度下降法对网络进行训练。在每一个batch中，计算样本经过网络的输出，即前向传播输出，随后计算其与球心之间的距离：
[0034][0035]
对每个batch中的进行由大到小的排序，取出每个batch中最大的距离d
max
进行误差反向传播。反向传播的过程中采用adam优化器来更新梯度。
[0036]
adam优化器的梯度更新公式为：
[0037][0038]
其中和为一阶动量和二阶动量的偏置校正项。
[0039]
最后采用随机梯度下降法对球心进行优化，球心梯度的变化公式：
[0040][0041]
其中l为初始学习率。
[0042]
当损失函数收敛之后，得到神经网络的最优权重ω和优化后的球心c。
[0043]3‑
3.计算单分类器阈值。
[0044]
将得到的误差距离进行从大到小排序,得到将得到的误差距离进行从大到小排序,得到其中和分别表示最大和最小的误差距离。设置一个阈值参数μ，得到阈值为θ＝ε
floor(μ
·
n)
。
[0045]
步骤4、对未知信号进行预测。
[0046]
对于未知声音信号x
p
将信号x
p
经过分帧、加窗处理之后转换成语谱图，将裁剪好的语谱图送入构建好的深度卷积神经网络，得到输出为然后计算出信号x
p
与球心的距离：
[0047][0048]
根据决策函数判断出未知样本的类别,取步骤3的θ作为分类决策阈值。决策函数如下：
[0049][0050]
本发明有益效果如下：
[0051]
本发明建立的min
‑
max深度卷积神经网络模型，可以针对不同类别的城市噪声进行训练并且准确识别新的类型的城市噪声。当在已有的城市噪声样本库中添加新类型样本时，不需要再对原有的样本进行训练，从而明显减少模型训练时间。本发明通过对每一种新出现的城市噪声建立单分类深度神经网络模型，获取包围同一类声音数据的超球面，来解
决无法穷举各种声音类型的问题。随后，构建深度神经网络，提升模型对城市噪声信号的表示能力，提升监测性能。最后构建min
‑
max单分类损失函数，通过对超球面半径隐式地约束，提升模型性能。
附图说明
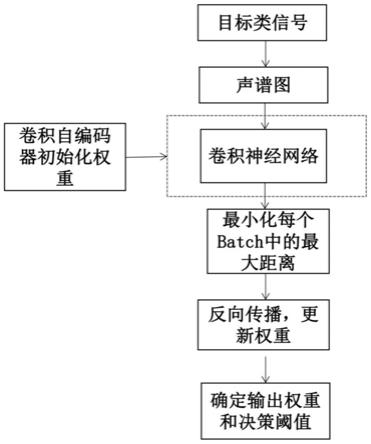
[0052]
图1是本发明提出的一种基于深度min
‑
max单分类神经网络的城市噪声识别方法的流程图；
[0053]
图2是搭建的神经网络模型结构图；
[0054]
图3是在imagenet上预训练好的vgg19模型结构图；
具体实施方式
[0055]
下面结合附图和实施例对本发明作进一步说明。
[0056]
以11种城市噪声信号为例，使用上述步骤2中搭建好的深度卷积神经网络对城市噪声信号语谱图进行训练，对本发明作进一步说明。以下描述仅作为示范和解释，并不对本发明作任何形式上的限制。
[0057]
如图1所示，基于深度min
‑
max单分类神经网络的城市噪声识别方法，具体实现如下：
[0058]
步骤1、采集11类城市噪声信号作为样本。对采集到的每一类城市噪声信号进行预处理，包括去噪，分帧和加窗，其中帧长为1024，帧移为512。将处理后的噪声信号转换成声谱图。
[0059]
步骤2、假设有5000个样本，将所有裁剪好的声谱图组成训练数据集x
n
×
k
＝[x1,
…
x
n
]。
[0060]
对于方式1：网络包括3个卷积块，每个卷积快的具体构成如下：
[0061]
卷积层卷积核的个数为6，大小5*5，步长为s＝1，填充p＝2。池化层的卷积块大小为2*2，步长为s＝1，填充p＝2。数据归一化层使用2维批量标准化函数，激活函数使用线性整流函数relu，卷积块的最后与全连接层相连，经过全连接层输出128*1的特征向量。
[0062]
取其中一个卷积块作为卷积自编码器的编码器，将训练数据集x
n
×
k
＝[x1,
…
x
n
]送入自编码器训练，训练过程中初始学习率设为0.001，迭代次数为50。将卷积自编码器训练好的网络权重，作为构建好的卷积神经网络每个卷积块的初始权重。
[0063]
网络权重初始化之后，训练样本x
n
×
k
＝[x1,
…
x
n
]。c初始值取x
n
×
k
＝[x1,
…
x
n
]第一次前向传播后输出的均值，计算公式如下：
[0064][0065]
α
i
是样本经过网络输出后得到的128*1的向量。
[0066]
对于方式2：采用在imagenet上预训练好的vgg19作为深度卷积神经网络。对预训练好的vgg19网络的输出层进行调整，删除最后一层全连接层后的softmax层。特征经过全连接层之后，网络直接输出128*1的特征向量。将在imagenet上预训练的网络结构的输出层进行修改，然后对所有样本进行训练。c初始值取第一次前向传播后输出结果的均值，计算公式同上。
[0067]
步骤3、在步骤2的基础上构建单分类min
‑
max损失函数，训练神经网络权重、单分类超球面球心、以及决策阈值。
[0068]
单分类min
‑
max损失函数如下：
[0069][0070]
其中，每一个batch的样本个数m为200。经过映射后，得到5000个大小为128*1的向量。min
‑
max损失函数通过最小化每个batch中样本到球心最大的距离来更新网络权重ω。是将样本映射到超球面的函数。c是步骤2得到超球面的初始球心。
[0071]
训练的过程中采用梯度下降法和反向传播算法。计算出每一个batch中200个样本经过神经网络输出并计算和球心之间的距离，公式如下：
[0072][0073]
采用梯度下降法对球心进行优化，球心梯度的变化公式：
[0074][0075]
其中l为初始学习率。
[0076]
将每个batch中200个样本的距离进行由大到小的排序，得d＝[d1,
…
d
200
]。取出每个batch中最大的距离为d
max
，其中d
max
是128*1的向量。网络的参数每训练一轮，将每个batch中的d
max
作为损失进行反向传播。一共25个batch，每一轮训练都对25个d
max
作反向传播，并采用adam优化器来更新梯度。
[0077]
在梯度反向传播进行更新的过程中，初始学习率设为0.0001，训练轮数设为200轮。为了平衡模型的训练速度和震荡问题。我们采用学习率指数衰减的方式来调整学习率。随着训练的进行，不断地调小学习率，以防模型出现震荡。学习率的更新方式如下：
[0078]
adaptive_learning_rate＝learning_rate*decay_rate
[0079]
其中，decay_rate等于训练总的步数除于衰减的步数。当权重经过200次迭代更新之后，损失函数收敛，此时得到最优权重ω与优化后的球心c。
[0080]
步骤4、计算单分类器阈值。
[0081]
将得到的误差距离进行从大到小排序,得到其中和分别表示最大和最小的误差距离。设置一个阈值参数μ，得到阈值为θ＝ε
floor(μ
·
n)
。
[0082]
步骤5、对未知信号进行分类预测。
[0083]
对于未知声音信号x
p
，将信号x
p
经过分帧加窗处理之后转换成语谱图，将其裁剪好的向量送入构建好的深度卷积神经网络进行训练，经过输出后得到特征向量然后计算特征向量与优化后球心的距离：
[0084][0085]
根据决策函数判断出未知样本的类别,取步骤4的θ作为分类决策阈值。
[0086]
决策函数如下：
[0087]