1.本发明属于数控加工技术领域，具体涉及一种考虑奇异点与碰撞避免的高阶光滑机器人曲面加工过程优化方法。


背景技术：

2.随着3d打印以及成型技术的不断进步，被加工零件逐渐向一体化复杂化发展，同时留给后续加工的去除量也越来越少，这些都促进了加工装备逐渐向轻量化灵巧化方向发展。而6r关节机器人随着其本身机械制造技术与电气控制技术的发展，其运动精度与平稳性也有了较大的提升，进一步促进了机器人作为执行装备在制造链中去除加工的应用。但是由于机器人驱动关节与工作空间复杂的映射关系、冗余的自由度、低刚度以及在工作空间随位置变化的机械特性，使得简单地将常规机器人直接应用到加工过程中，难以满足加工精度的要求。
3.因此需要对机器人加工运行过程进行深入分析，并研究机器人运动过程对加工精度的影响规律。尤其是针对机器人加工过程中存在冗余自由度所体现的灵活性问题，需要从冗余自由度中对机器人加工过程的几何轨迹进行寻优。
4.大量的国内外研究学者也在机器人加工领域开展了大量研究。欧盟于2010年、2012年先后启动comet和hephestos计划，旨在利用工业机器人实现路径规划、轨迹生成以及跟踪控制来完成难加工材料的机器人加工，涵盖铣削、磨削和抛光等领域。abb、kuka等公司已经推出铣削加工机器人以及相应的机器人轨迹软件生成包。
5.国际生产工程科学院(cirp，the international academy for production engineering)在2019年报中，多名国际知名专家对机器人加工研究发表了综述文章(参考文献1：verl,alexander,anna valente,shreyes melkote,christian brecher,erdem ozturk,and lutfi taner tunc."robots in machining."cirp annals 68,no.2(2019):799-822.)，阐述了机器人作为加工装备的广阔应用前景与需要解决的科研问题。
6.国内华中科技大学与上海交通大学在机器人抛光与打磨等应用领域有大量的研究。丁汉院士团队在大型构件多机器人智能加工方面，提出了新的应用方法，做出了大量科研创新成果。
7.清华大学刘辛军团队在机器人系统的结构设计、机器人化制造装备进行了系统研究。
8.针对如何找到最优轨迹问题，已有公开技术从冗余自由度中寻找光滑且满足空间约束要求的机器人曲面加工关节轨迹。
9.彭等(参考文献2：peng j f,dingy,zhang g,et al.smoothness-orientedpath optimization for robotic milling processes.sci.china technol.sci.,2020,63:1751
–
1763.)采用序列线性化优化方法对传统的基于图的方法提供的初始解进行改进，从冗余自由度中获得平滑轨迹。
10.卢等(参考文献3：lu y a,tang k,wang c y.collision-free and smooth joint motion planning for six-axis industrial robots by redundancy optimization.robotics and computer-integrated manufacturing,2021,68:102091.)采用b样条曲线插值表征关节轨迹曲线。他们提出了一种优化方法来解决6r机器人的逆运动学问题，以遵循给定的刀具路径，同时考虑平滑度和无碰撞要求。
11.然而，在上述方法中，仅考虑了一个冗余自由度，即刀具沿其自身轴线的旋转。但对于大多数球端面加工过程，存在三个冗余自由度，刀具的三个旋转自由度是自由的。
12.考虑到基于采样方法在机器人轨迹规划中有效性，已有公开技术采用基于采样的机器人关节轨迹规划方法规划机器人曲面加工轨迹。diaz posada(参考文献4：julian d p,ulrich s,arjun s,et al.automatic motion generation for robotic milling optimizing stiffness with sample-based planning.machines,2017,5(1):3-3.)从冗余的自由度中沿着规划的刀尖点轨迹，采用transition-rrt基于采样的规划方法，寻找刚度较大的刀具姿态轨迹，从而得到机器人关节空间轨迹。
13.合肥工业大学在cn112947298a公开了一种机器人曲面加工轨迹优化生成方法、系统及终端。采用基于采样的机器人运动规划方法对机器人球头铣削与侧铣加工进行关节轨迹优化，从而求得路程最短轨迹。但是基于采样的轨迹规划方法，较难考虑关节光滑性的需求，以及计算时间较长，难于收敛到最优轨迹等问题。


技术实现要素：

14.本发明的目的在于解决现有技术的不足，提供一种一种考虑奇异点与碰撞避免的高阶光滑机器人曲面加工过程优化方法；具体而言，针对机器人加工自由曲面零件，生成一种考虑刀轴矢量约束以及奇异点避免的机器人曲面加工高阶光顺轨迹。该方法首先生成刀具位置轨迹，然后对刀具姿态轨迹的微分向量进行优化，并进行逐步积分，最终生成刀具整体姿态轨迹。在刀具姿态微分向量优化的过程中，考虑刀具的碰撞约束以及奇异点避免的要求，使加工过程中的刀具姿态远离这些区域。同时在积分过程中，考虑刀具姿态微分向量的变化率，保证生成的刀具轨迹具有高阶光顺性。
15.本发明是通过以下技术方案实现：
16.一种考虑奇异点避免的高阶光滑机器人曲面加工过程优化方法，适用于机器人数控加工领域，其特征在于方法步骤如下：
17.(1)根据被加工零件曲面特征，以及加工要求，生成零件的刀触点轨迹以及刀轴矢量的约束范围，最终生成刀具位置轨迹；
18.(2)沿刀具位置轨迹，对刀具姿态微分向量进行优化，并根据给定的刀具姿态初值，通过不断积分得到整体的刀具姿态轨迹；
19.(3)在采用刀具姿态向量逐步积分的过程中，对刀具姿态微分向量的变化率进行限制，保证规划出轨迹的高阶光顺性；
20.(4)在刀具姿态微分向量优化的过程中，优化目标充分考虑：刀轴矢量约束、奇异点避免约束以及碰撞约束要求，并构建微分向量的组合优化目标，协调各个约束要求；
21.(5)对刀具姿态向量的边界进行光顺预处理，保证本发明所提方法处理约束突变能力。
22.进一步限定的技术方案如下：
23.根据所提方法的步骤(2)：沿刀触点轨迹，对刀具姿态微分向量进行优化，并根据给定的刀具姿态初值，通过不断积分得到整体的刀具姿态轨迹，其特征在于：
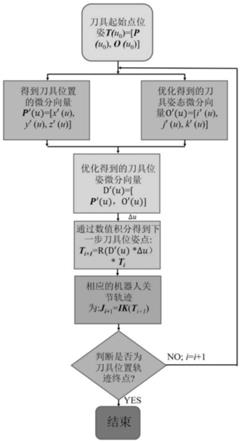
24.在刀具位置轨迹p(u)初始点处p(u0)，根据得到的刀具姿态约束范围，选择初始刀具姿态向量o(u0)，选择的原则应尽量远离刀具姿态约束的边界，并避免碰撞与奇异。然后对刀具姿态沿刀具位置轨迹p(u)的导数o'(u0)＝[δx/δu,δy/δu,δz/δu]进行优化，并根据得到的优化刀具姿态微分向量沿刀具位置轨迹p(u)进行数值积分，得到下一点刀具姿态向量o(u1)。重复上述过程直至刀具位置轨迹p(u)终点，得到沿刀具位置曲线的刀具姿态轨迹o(u)，从而得到刀具整体位姿轨迹t(u)＝[p(u),o(u)]。方法整体流程如附图1所示：
[0025]
根据所提方法的步骤(3)采用刀具姿态向量逐步积分的过程中，对刀具姿态微分向量及其变化率进行限制，保证规划出轨迹的高阶光顺性，其特征在于：
[0026]
为了保证规划的刀具姿态光顺性，刀具姿态沿刀具位置轨迹p(u)的导数o'(u)＝[δx/du,δy/du,δz/du]，作为优化变量o'(u0)，需要限定其变化范围。即：
[0027][0028][0029][0030]
δx/du,δy/du,δz/du,与为优化变量o'(u)的上下界。即在第i步的优化过程中，优化变量o'(ui)＝[δx/du(ui),δy/du(ui),δz/du(ui)]的变量范围，分别为
[0031][0032][0033][0034]
为了进一步保证规划的刀具姿态光顺性，对刀具姿态微分向量的变化量，进一步约束，即限定o”(u)＝[δx2/d2u,δy2/d2u,δz2/d2u]的变化范围：
[0035][0036][0037][0038]
δx2/d2u,δy2/d2u,δz2/d2u,与为优化变量变化率o”(u)的上下界。即在第i步的优化过程中，优化变量的差分应满足
[0039]
[0040][0041][0042]
当第i+1步优化变量变化率o”(u
i+1
)大于给定的约束范围时。第i+1步优化变量o'(u
i+1
)需要重新计算。以δx/du(u
i+1
)为例，重计算方法如下：
[0043]
方法1:
[0044]
根据优化目标，得到的优化变量为δx
i+1
；
[0045]
如果
[0046]
δx/du(u
i+1
)＝δx2/d2u*δ+δx/du(ui)
[0047]
否则
[0048]
如果
[0049]
δx/du(u
i+1
)＝δx2/d2u*δ+δx/du(ui)
[0050]
否则
[0051]
结束
[0052]
结束
[0053]
根据所提方法的步骤(4)在刀具姿态微分向量优化的过程中，优化目标充分考虑：刀轴矢量碰撞约束以及奇异点避免要求，并构建微分向量的组合优化目标，协调各个约束要求，其特征在于：
[0054]
(1)保证关节空间微分向量最小
[0055]
在每一步的刀具姿态微分向量o'(u)＝[δx/du,δy/du,δz/du]的优化过程中，保证关节空间机器人关节轴的微分向量dq最小。构建优化目标与优化变量的关系为：
[0056]
min obj_1(δx/du,δy/du,δz/du)＝||dq|| (5)
[0057]
根据雅可比矩阵j定义，得到关节微分向量dq与刀具位姿向量d＝[p’(u),o’(u)]du的关系为：
[0058]dq
＝jd (6)
[0059]
在实际数值积分过程中，将刀具位姿微分向量d＝[p’(u),o’(u)]du差分化，即：d＝[p’(u),o’(u)]δu则构建的优化目标为：
[0060]
min obj_1(δx/du,δy/du,δz/du)＝||jd|| (7)
[0061]
(2)刀轴矢量及碰撞约束要求
[0062]
根据加工过程要求，刀轴矢量需要限定在一定的范围内，保持加工质量的一致性。即对于积分中的第i步，在沿刀具轨迹的坐标系下，刀具的姿态角度[α(ui),β(ui),γ(ui)](α为刀具刀轴矢量z
tool
在局部坐标系下局部坐标系xoy内投影与局部坐标系x轴的夹角，β为刀具刀轴矢量z
tool
绕自身旋转轴的旋转角度，γ为刀具刀轴矢量在局部坐标系下与局部坐标系z轴的夹角。)需要限定在一定范围内。
[0063]
[0064]
除了切削角度的要求外，机器人以及切削主轴的碰撞约束要求，也可以转换为轨迹坐标系下的刀具姿态角度[α(ui),β(ui),γ(ui)]约束。
[0065]
为了避免使刀具姿态角度超出约束要求，优化的刀具姿态微分向量o'(u)应使得刀具姿态角度微分运行方向指向可行域的中心在i步积分中，切削角度α(ui)与γ(ui)为
[0066]
α(ui)＝acos(dot(proj(z
tool_i
),xi))
[0067]
γ(ui)＝acos(dot(z
tool_i
,zi))
[0068]
ꢀꢀ
(9)
[0069]
相对应在i+1点处切削角度α与γ为
[0070]
α(u
i+1
)＝acos(dot(proj(z
tool_i+1
),x
i+1
))
[0071]
γ(u
i+1
)＝acos(dot(z
tool_i+1
,z
i+1
))
[0072]
ꢀꢀꢀ
(10)
[0073]
则α与γ角度的变化δα＝α(u
i+1
)-α(ui)，δγ＝γ(u
i+1
)-γ(ui)为
[0074][0075]
δγ＝acos(dot(z
tool_i+1
,z
i+1
))-acos(dot(z
tool_i
,zi)) (11)
[0076][0077]
设i处的刀具位姿为ti＝[x
tool
,y
tool
,z
tool
,p
tool
]i，根据刀具位姿的微分向量d，是第i+1点出的刀具位姿t
i+1
＝[x
tool
,y
tool
,z
tool
,p
tool
]
i+1
为：
[0078]
t
i+1
＝r(d*δu)tiꢀꢀꢀꢀꢀ
(12)
[0079]
式中r(d)为微分向量d的齐次坐标变换矩阵。则由微分向量d引起的δα，δγ为
[0080]
δα＝acos(dot(proj(r(d)
ztool_i
),x
i+1
))-acos(dot(proj(z
tool_i
),xi))
[0081]
δγ＝acos(dot(r(d)z
tool_i
,z
i+1
))-acos(dot(z
tool_i
,zi))
[0082]
ꢀꢀꢀꢀ
(13)
[0083]
根据当前切削角度α(ui)和γ(ui)，需要δα，δγ变化使的α(u
i+1
)和γ(u
i+1
)朝向可行域的中心。加工过程刀具角度要求为：
[0084][0085][0086]
式中和是可行域的中心点，根据上式无论α(ui)与γ(ui)大于或小于α
hf_i
和γ
hf_i
，优化目标obj_2(δx/du,δy/du,δz/du)和obj_3(δx/du,δy/du,δz/du)的最小值都会使得α(u
i+1
)和γ(u
i+1
)通过δα与δγ朝和变化。
[0087]
(3)奇异点避免约束要求
[0088]
为了避免加工过程中机器人进入奇异状态，优化变量刀具姿态微分向量o'(u)应使得机器人运动尽量远离机器人奇异点区域。机器人的奇异点表征采用机器人雅可比矩阵的条件数作为表征。
[0089]
κ(q)＝||j(q)-1
||
∞
||j(q)||
∞
ꢀꢀꢀꢀ
(15)
[0090]
式中||
·
||
∞
为无穷范数，j(q)为机器人关节变量为q时的雅可比矩阵。条件数的变化范围为：1≤κ(j)≤∞。条件数κ(q)数值越大，表明机器人的状态越接近奇异状态。当条件数κ(j)＝∞时，机器人处于奇异状态。因此优化变量刀具姿态微分向量o'(u)应使得机器人条件数往较小的地方移动。
[0091]
关节微分向量dq与刀具位姿向量d＝[p’(u),o’(u)]du的关系为：
[0092]dq
＝jd (16)
[0093]
则根据当前机器人的关节变量qi,根据微分向量d估计的下一点机器人关节变量
[0094][0095]
从而得到的估计的机器人雅可比矩阵与相应的条件数在实际数值积分过程中，将积分参数的微分变化du变为积分步长δu。则刀具位姿向量d＝[p’(u),o’(u)]δu。因此，相应优化目标为:
[0096][0097]
(4)组合优化目标
[0098]
考虑到以上各个优化目标，需要对各个优化目标进行整合。整合的优化目标，如下式所示：
[0099]
min objective(δx/du,δy/du,δz/du)＝λ1obj_1
unit
+λ2obj_2
unit
+λ3obj_3
unit
+λ4obj_4
unit
ꢀꢀꢀꢀꢀ
(19)
[0100][0101]
式中obj_1
unit
，obj_2
unit
，obj_3
unit
和obj_4
unit
是归一化的优化目标。
[0102][0103][0104][0105][0106]
归一化后的优化目标都是在优化变量可行域内，从最小值0，变化到最大值1。
[0107]
λ1与系统状态无关，因此选择λ1为常数。当对obj_1
unit
要求比较高时，即：关节光滑性要求比较高时，可以选择较大的λ1。当对obj_1
unit
要求比较低时，即：关节光滑性要求比较低时，可以选择较小的λ1。
[0108]
考虑奇异点避免的影响，奇异点影响因子λ2需要与机器人奇异状态关联。当机器
人接近奇异点时，需要增加机器人奇异点影响因子λ2，使得obj_2
unit
在总体优化目标的份额中增加。设计机器人奇异点影响因子λ2如下：
[0109][0110]
式中a≥1是λ2的指数常数，κ
threshold
为机器人条件数的阈值。在本发明中，a的数值选择4，而κ
threshold
的数值选择100。
[0111]
对于刀轴矢量角度约束要求obj_3
unit
与obj_4
unit
，也与刀轴矢量角度的状态有关系。当刀轴矢量离刀轴约束边缘较远时，λ3与λ4应选择较小值，使得obj_3
unit
与obj_4
unit
在总体优化目标的份额中减小。当刀轴矢量接近刀轴约束边缘时，λ3与λ4应选择较大值，使得obj_3
unit
与obj_4
unit
在总体优化目标的份额中增加。设计的刀轴矢量约束影响因子λ3与λ4如下：
[0112][0113][0114]
式中αi与γi为第i步积分的刀轴矢量角度；αh与γh为刀轴矢量约束的中心；a1与a2是大于2的系数；b1与b2是大于2的指数。当刀轴矢量角度约束要求严格时，a1，a2，b1与b2取较大值。从式中可以看出，当αi与γi靠近约束边界时，λ3与λ4将增大，从而使得obj_3
unit
与obj_4
unit
在总体优化目标的份额中增加。
[0115]
根据所提方法的步骤(5)对刀具姿态向量的边界进行光顺预处理，保证本发明所提方法处理约束突变能力，其特征在于：
[0116]
(1)根据曲线曲率特征对刀具刀轴矢量边界进行预调整
[0117]
由于刀轴矢量角度定义在局部坐标系下，当刀尖点轨迹曲率变化较大时，刀具角度会因此变化从而违反约束。因此刀具角度边界约束α,和γ需要进行预先调整，为刀具曲线变化引起的刀轴矢量角度突变，提供裕度。首先定义曲线角度变化评价指标(相邻积分步骤中局部坐标系坐标轴的夹角，)。当评价指标大于给定的约束上限时|δ/ds|，相应的边界需要进行预处理，从而预调整刀轴矢量，使得刀轴矢量不超出边界要求。具体刀具边界预调整方法如下：
[0118]
方法2:
[0119]
①
令α0＝α,γ0＝γ；
[0120]
②
从刀尖点轨迹的起点u0开始；
[0121]
③
计算刀尖点轨迹ui曲线角度变化评价指标
[0122]
④
如果
[0123]
在ui点处相应的约束下界α
0_i
或γ
0_i
更改为
[0124]
或
[0125][0126]
否则
[0127]
如果
[0128]
在ui点处相应的约束上界或更改为
[0129]
或
[0130][0131]
否则
[0132]
结束
[0133]
结束
[0134]
⑤
判断i《n
[0135]
i＝i+1；
[0136]
返回步骤
③
；
[0137]
否则
[0138]
结束
[0139]
(2)根据刀具角度边界，光顺边界变化率
[0140]
在本发明中，优化的变量为刀具姿态的微分向量，且其变化率也受到了方法1的限制。因此刀轴矢量的变化较为平缓，而约束边界由于碰撞等约束的存在，使得边界会出现较为剧烈的突变。因此需要对刀具角度边界约束α,和γ进行预光滑处理，使得在刀具轨迹积分前进的方向上保证变化率不超微分向量的最大变化率。
[0141]
在本发明中，设置为边界变化率的指标,其中boui为在ui处的边界值,si是从u0到ui点的刀尖点轨迹弧长。边界变化率评价指标为该评价指标通过优化微分向量的边界(δx/ds,δy/ds,δz/ds,和)进行确定，即：
[0142][0143]
式中θ为x,y与z。具体的边界光滑方法如下：
[0144]
方法3
[0145]
①
从刀尖点轨迹的终点un；
[0146]
②
算在ui点处的边界变化率
[0147]
③
如果
[0148][0149]
否则
[0150]
结束
[0151]
④
如果i-1》0
[0152]
i＝i-1；
[0153]
返回
②
；
[0154]
否则
[0155]
结束
[0156]
对于约束下界，步骤
③
变为:
[0157]
③
如果
[0158][0159]
否则
[0160]
结束
[0161]
本技术的有益效果在于：
[0162]
(1)本发明开发了一种考虑刀轴矢量约束以及奇异点避免的高阶光滑轨迹生成方法，提高机器人曲面加工过程的光顺性，提高了加工效率；
[0163]
(2)本发明对优化的刀具姿态微分向量的变化率，进一步进行了约束，生成了高阶光顺性曲面加工轨迹，提高了加工效率与精度；
[0164]
(3)本发明采用机器人关节空间微分向量模的大小作为优化目标，进一步降低了机器人关节空间的运行距离，提高了关节空间运动平稳性；
[0165]
(4)本发明考虑了刀轴矢量约束，使得加工过程中，刀具切削角度能够限定在一定范围内，保证加工条件的一致性；
[0166]
(5)本发明考虑了刀具碰撞约束，并将碰撞约束转换成了刀轴矢量约束，避免了刀具的碰撞；
[0167]
(6)本发明考虑了机器人奇异性要求，使得机器人曲面加工过程，避免进入奇异性区域。
附图说明
[0168]
下面结合附图中的实施例对本技术作进一步的详细说明，但并不构成对本技术的任何限制。
[0169]
图1为本发明的整体方法流程。
[0170]
图2为机器人加工系统。
[0171]
图3为被加工轨迹。
[0172]
图4为刀具姿态角度约束图。
[0173]
图5为预处理后的刀具姿态角度约束图。
[0174]
图6为各个方法规划的关节一轨迹图。
[0175]
图7为各个方法规划的关节二轨迹图。
[0176]
图8为各个方法规划的关节三轨迹图。
[0177]
图9为各个方法规划的关节四轨迹图。
[0178]
图10为各个方法规划的关节五轨迹图。
[0179]
图11为各个方法规划的关节六轨迹图。
[0180]
图12为各个方法规划的刀轴矢量角度α。
[0181]
图13为各个方法规划的刀轴矢量角度γ。
[0182]
图14为各个方法规划的雅克比矩阵条件数图。
[0183]
图15为规划的刀具位姿曲线图。
具体实施方式
[0184]
下面结合附图，通过实施例对本发明作进一步地描述。
[0185]
以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进。这些都属于本发明的保护范围。以下结合附图对本发明的实施详细说明，但本发明的保护范围不限于下述的实施例。
[0186]
如图1所示，考虑奇异点与碰撞避免的高阶光滑机器人曲面加工关节轨迹生成方法的具体流程包括：首先根据被加工零件曲面特征，以及加工要求，生成零件的刀触点轨迹以及刀轴矢量的约束范围，最终得到刀具位置轨迹；沿刀具位置轨迹，对刀具姿态微分向量进行优化，并根据给定的刀具姿态初值，通过不断积分得到整体的刀具姿态轨迹；在每步刀具姿态向量逐步积分的过程中，对刀具姿态微分向量的变化率进行限制，保证规划出轨迹的高阶光顺性；在刀具姿态微分向量优化的过程中，优化目标充分考虑：刀轴矢量约束、奇异点避免约束以及碰撞约束要求，并构建微分向量的组合优化目标，协调各个约束要求；对刀具姿态向量的边界进行光顺预处理，保证本发明所提方法处理约束突变能力。
[0187]
本实施例所使用机器人为ur-5机器人包括实时机器人控制器与机器人本体，机器人本体包括六个关节轴以及末端电机主轴。机器人关节参数以及工件与刀具坐标系关系如下：
[0188]
表1ur-5机器人的d-h参数
[0189][0190]
工件坐标系{wcs}相对于机器人坐标系{rcs}的位置关系矩阵，刀尖点到机器人关节末端的关系矩阵为:
[0191]
[0192]
加工机器人如2所示。
[0193]
采用如附图3所示的一个方形轨迹进行实施例验证。该方形轨迹的边长为200mm。同时为了验证本发明所提方法，沿刀具轨迹存在四个障碍物。同时根据切削加工要求，给出刀具角度在局部坐标系下的约束范围90
°
≤α≤270
°
,5
°
≤γ≤45
°
从而得到刀轴矢量在局部坐标系下的约束范围如附图4所示。
[0194]
根据所提方法的步骤(5)对刀具姿态向量的边界进行光顺预处理，保证本发明所提方法处理约束突变能力。
[0195]
(1)根据曲线曲率特征对刀具刀轴矢量边界进行预调整
[0196]
由于刀轴矢量角度定义在局部坐标系下，当刀尖点轨迹曲率变化较大时，刀具角度会因此变化从而违反约束。因此刀具角度边界约束α,和γ需要进行预先调整，为刀具曲线变化引起的刀轴矢量角度突变，提供裕度。首先定义曲线角度变化评价指标(相邻积分步骤中局部坐标系坐标轴的夹角，)。当评价指标大于给定的约束上限时|δ/ds|，相应的边界需要进行预处理，从而预调整刀轴矢量，使得刀轴矢量不超出边界要求。具体刀具边界预调整方法如说明书方法2所述。
[0197]
(2)根据刀具角度边界，光顺边界变化率
[0198]
在本发明中，优化的变量为刀具姿态的微分向量，且其变化率也受到了方法1的限制。因此刀轴矢量的变化较为平缓，而约束边界由于碰撞等约束的存在，使得边界会出现较为剧烈的突变。因此需要对刀具角度边界约束α,和γ进行预光滑处理，使得在刀具轨迹积分前进的方向上保证变化率不超优化微分向量的最大变化率。
[0199]
在本发明中，设置为边界变化率的指标,其中boui为在ui处的边界值,si是从u0到ui点的刀尖点轨迹弧长。边界变化率评价指标为该评价指标通过优化微分向量的边界(δx/ds,δx/ds,δx/ds,和)进行确定，即：
[0200][0201]
式中θ为x,y与z。具体的边界光滑方法如说明书方法3所述。
[0202]
预光滑与调整后的刀具角度约束如附图5所示。
[0203]
所提方法的步骤(4)在刀具姿态微分向量优化的过程中，构建的优化目标充分考虑：刀轴矢量碰撞约束以及奇异点避免要求，并构建微分向量的组合优化目标，协调各个约束要求。
[0204]
(1)保证关节空间微分向量最小
[0205]
在每一步的刀具姿态微分向量o'(u)＝[δx/du,δy/du,δz/du]的优化过程中，保证关节空间机器人关节轴的微分向量dq最小。构建优化目标与优化变量的关系为：
[0206]
min obj_1(δx/du,δy/du,δz/du)＝||dq||
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0207]
根据雅可比矩阵j定义，得到关节微分向量dq与刀具位姿向量d＝[p’(u),o’(u)]du的关系为：
[0208]dq
＝jd
ꢀꢀꢀꢀꢀꢀ
(3)
[0209]
在实际数值积分过程中，将刀具位姿微分向量d＝[p’(u),o’(u)]du差分化，即：d＝[p’(u),o’(u)]δu则构建的优化目标为：
[0210]
min obj_1(δx/du,δy/du,δz/du)＝||jd|| (4)
[0211]
(2)刀轴矢量及碰撞约束要求
[0212]
根据加工过程要求，刀轴矢量需要限定在一定的范围内，保持加工质量的一致性。即对于积分中的第i步，在沿刀具轨迹的坐标系下，刀具的姿态角度[α(ui),β(ui),γ(ui)](α0为刀具刀轴矢量z
tool
在局部坐标系下局部坐标系xoy内投影与局部坐标系x轴的夹角，β0为刀具刀轴矢量z
tool
绕自身旋转轴的旋转角度，γ0为刀具刀轴矢量在局部坐标系下与局部坐标系z轴的夹角。)需要限定在一定范围内。
[0213][0214]
除了切削角度的要求外，机器人以及切削主轴的碰撞约束要求，也可以转换为轨迹坐标系下的刀具姿态角度[α(ui),β(ui),γ(ui)]约束。
[0215]
为了避免使刀具姿态角度超出约束要求，优化的刀具姿态微分向量o'(u)应使得刀具姿态角度微分运行方向指向可行域的中心在i步积分中，切削角度α(ui)与γ(ui)为
[0216]
α(ui)＝acos(dot(proj(z
tool_i
),xi))
[0217]
γ(ui)＝acos(dot(z
tool_i
,zi))
[0218]
ꢀꢀꢀꢀ
(6)
[0219]
相对应在i+1点处切削角度α与γ为
[0220]
α(u
i+1
)＝acos(dot(proj(z
tool_i+1
),x
i+1
))
[0221]
γ(u
i+1
)＝acos(dot(z
tool_i+1
,z
i+1
))
[0222]
ꢀꢀꢀꢀ
(7)
[0223]
则的α与γ角度的变化δα＝α(u
i+1
)-α(ui)，δγ＝γ(u
i+1
)-γ(ui)为
[0224][0225]
δγ＝acos(dot(z
tool_i+1
,z
i+1
))-acos(dot(z
tool_i
,zi))
ꢀꢀꢀꢀꢀ
(8)
[0226][0227]
设i处的刀尖点位姿为ti＝[x
tool
,y
tool
,z
tool
,p
tool
]i，根据刀具位姿的微分向量d，是第i+1点出的刀尖点姿态t
i+1
＝[x
tool
,y
tool
,z
tool
,p
tool
]
i+1
为：
[0228]
t
i+1
＝r(d*δu)tiꢀꢀꢀꢀꢀ
(9)
[0229]
式中r(d)为微分向量d的齐次坐标变换矩阵。则由微分向量d引起的δα，δγ为
[0230]
δα＝acos(dot(proj(r(d)z
tool_i
),x
i+1
))-acos(dot(proj(z
tool_i
),xi))
[0231]
δγ＝acos(dot(r(d)z
tool_i
,z
i+1
))-acos(dot(z
tool_i
,zi))
[0232]
ꢀꢀꢀꢀꢀꢀ
(10)
[0233]
根据当前切削角度α(ui)和γ(ui)，需要δα，δγ变化使的α(u
i+1
)和γ(u
i+1
)朝向可行域的中心。加工过程刀具角度要求为：
[0234]
[0235][0236]
式中和是可行域的中心点，根据上式无论α(ui)与γ(ui)大于或小于α
hf_i
和γ
hf_i
，优化目标obj_2(δx/du,δy/du,δz/du)和obj_3(δx/du,δy/du,δz/du)的最小值都会使得α(u
i+1
)和γ(u
i+1
)通过δα与δγ朝和变化。
[0237]
(3)奇异点避免约束要求
[0238]
为了避免加工过程中机器人进入奇异状态，优化变量刀具姿态微分向量o'(u)应使得机器人运动尽量远离机器人奇异点区域。机器人的奇异点表征采用机器人雅可比矩阵的条件数作为表征。
[0239]
κ(q)＝||j(q)-1
||
∞
||j(q)||
∞ (12)
[0240]
式中||
·
||
∞
为无穷范数，j(q)为机器人关节变量为q时的雅可比矩阵。条件数的变化范围为：1≤κ(j)≤∞。条件数κ(q)数值越大，表明机器人的状态越接近奇异状态。当条件数κ(j)＝∞时，机器人处于奇异状态。因此优化变量刀具姿态微分向量o'(u)应使得机器人条件数往较小的地方移动。
[0241]
关节微分向量dq与刀具位姿向量d＝[p’(u),o’(u)]du的关系为：
[0242]dq
＝jd (13)
[0243]
则根据当前机器人的关节变量qi,根据微分向量d估计的下一点机器人关节变量
[0244][0245]
从而得到的估计的机器人雅可比矩阵与相应的条件数在实际数值积分过程中，将积分参数的微分变化du变为积分步长δu。则刀具位姿向量d＝[p’(u),o’(u)]δu。因此，相应优化目标为:
[0246][0247]
(4)组合优化目标
[0248]
考虑到以上各个优化目标，需要对各个优化目标进行整合。整合的优化目标，如下式所示：
[0249]
min objective(δx/du,δy/du,δz/du)＝
[0250]
λ1obj_1
unit
+λ2obj_2
unit
+λ3obj_3
unit
+λ4obj_4
unit
ꢀꢀꢀꢀꢀꢀꢀ
(16)
[0251]
式中obj_1
unit
，obj_2
unit
，obj_3
unit
和obj_4
unit
是归一化的优化目标是归一化的优化目标
[0252]
归一化后的优化目标都是在优化变量可行域内，从最小值0，变化到最大值1。λ1与系统状态无关，因此选择λ1为常数。当对obj_1
unit
要求比较高时，即：关
节光滑性要求比较高时，可以选择较大的λ1。当对obj_1
unit
要求比较低时，即：关节光滑性要求比较低时，可以选择较小的λ1。
[0253]
考虑奇异点避免的影响，奇异点影响因子λ2需要与机器人奇异状态关联。当机器人接近奇异点时，需要增加机器人奇异点影响因子λ2，使得obj_2
unit
在总体优化目标的份额中增加。设计机器人奇异点影响因子λ2如下：
[0254][0255]
式中a≥1是λ2的指数常数，κ
threshold
为机器人条件数的阈值。在本发明中，a的数值选择4，而κ
threshold
的数值选择100。
[0256]
对于刀轴矢量角度约束要求obj_3
unit
与obj_4
unit
，也与刀轴矢量角度的状态有关系。当刀轴矢量离刀轴约束边缘较远时，λ3与λ4应选择较小值，使得obj_3
unit
与obj_4
unit
在总体优化目标的份额中减小。当刀轴矢量接近刀轴约束边缘时，λ3与λ4应选择较大值，使得obj_3
unit
与obj_4
unit
在总体优化目标的份额中增加。设计的刀轴矢量约束影响因子λ3与λ4如下：
[0257][0258][0259]
式中αi与γi为第i步积分的刀轴矢量角度；αh与γh为刀轴矢量约束的中心；a1与a2是大于2的系数；b1与b2是大于2的指数。当刀轴矢量角度约束要求严格时，a1，a2，b1与b2取较大值。从式中可以看出，当αi与γi靠近约束边界时，λ3与λ4将增大，从而使得，使得obj_3
unit
与obj_4
unit
在总体优化目标的份额中增加。
[0260]
根据每步优化得到的刀具姿态微分向量d
optimized
，通过数值积分得到下一点的刀具姿态轨迹。为了保证刀具姿态轨迹的高阶光顺性，根据所述步骤(3)采用刀具姿态向量逐步积分的过程中，对刀具姿态微分向量及其变化率进行限制。
[0261]
为了保证规划的刀具姿态光顺性，刀具姿态沿刀具位置轨迹p(u)的导数o'(u)＝[δx/du,δy/du,δz/du]，作为优化变量o'(u0)，需要限定其变化范围。即：
[0262][0263][0264][0265]
δx/du,δy/du,δz/du,与为优化变量o'(u)的上下界。即在第i步的优化过程中，优化变量o'(ui)＝[δx/du(ui),δy/du(ui),δz/du(ui)]的变量范围，分别为
[0266]
[0267][0268][0269]
为了进一步保证规划的刀具姿态光顺性，对刀具姿态微分向量的变化量，进行进一步约束，即限定o”(u)＝[δx2/d2u,δy2/d2u,δz2/d2u]的变化范围：
[0270][0271][0272][0273]
δx2/d2u,δy2/d2u,δz2/d2u,与为优化变量变化率o”(u)的上下界。即在第i步的优化过程中，优化变量的差分应满足
[0274][0275][0276][0277]
当第i+1步优化变量变化率o”(u
i+1
)大于给定的约束范围时。第i+1步优化变量o'(u
i+1
)需要重新计算。以δx/du(u
i+1
)为例，重计算方法如下：
[0278]
方法1:
[0279]
根据优化目标，得到的优化变量为δx
i+1
；
[0280]
如果
[0281]
δx/du(u
i+1
)＝δx2/d2u*δ+δx/du(ui)
[0282]
否则
[0283]
如果
[0284]
δx/du(u
i+1
)＝δx2/d2u*δ+δx/du(ui)
[0285]
否则
[0286]
结束
[0287]
结束
[0288]
根据得到的高阶变化率受约束的刀具姿态微分向量，通过不断地数值积分得到整体的刀具姿态轨迹，并经运动学逆解运算得到加工该曲面的机器人关节轨迹。
[0289]
为了体现本发明的有效性，除本发明所提方法，另外三种对比方法对相同刀尖点轨迹进行规划。第一种方法就是本发明提出的规划方法。第二种方法(nsc)是在整个刀具轨
迹规划中，刀轴矢量角度约束未光滑。第三种方法(fdl)是在整个刀具轨迹规划中，优化的微分向量变化率未限制。第四种方法(nso)是在整个刀具轨迹规划中，未考虑奇异点避免要求。
[0290]
首先各个方法规划的关节轨迹如附图6、图7、图8、图9、图10、图11所示。同时各个方法规划的刀具方位角度α和γ轨迹图如附图12和13所示。可以看出，采用nsc的方法，由于刀轴矢量约束未光滑处理，使得采用高阶微分向量积分得到的轨迹难以满足要求，存在超出约束的情况。而本发明所提方法与其他方法规划的刀具方位角度满足约束要求。所规划轨迹的雅可比矩阵条件数如附图14所示，结合机器人关节轨迹情况，采用nso方法规划的轨迹，存在奇异状态，即：机器人条件数在一定区域内显著增大。并且在该区域内，尽管刀具姿态只发生了轻微变化，但是机器人关节出现了较大变化。从而表明，本发明所提方法对奇异性的避免情况。规划的刀具姿态图，如附图15所示，从图中可以看出，本发明所提方法能够有效的避免障碍物。
[0291]
以上所举实施例为本技术的较佳实施方式，仅用来方便说明本技术，并非对本技术作任何形式上的限制，任何所属技术领域中具有通常知识者，若在不脱离本技术所提技术特征的范围内，利用本技术所揭示技术内容所作出局部更动或修饰的等效实施例，并且未脱离本技术的技术特征内容，均仍属于本技术技术特征的范围内。