1.本发明属于电容耦合电阻层析成像技术领域，具体涉及一种电容耦合电阻层析成像图像重建方法，即通过新型的全变分正则化方法实现电容耦合电阻层析成像图像的重建。


背景技术：

2.电学层析成像技术(electrical tomography，et)出现于二十世纪八十年代后期，是一种基于电学特性(电导率/介电系数/磁导率/复导纳)敏感机理的过程层析成像技术。它通过边界测量值得出被测区域内介质的分布信息，运用相应的成像算法，进而对电学特性的分布信息进行成像。电学层析成像常用于工业检测领域，在生物医学成像领域也有很大的应用前景。与其他成像技术相比，电阻层析成像具有产生高分辨率图像的优点，同时具有无辐射、无侵入、相对较低的成本、快速响应和结构简单等优点。然而，在传统的电阻层析成像中，电极和导电介质之间的直接接触会引发问题。电阻层析成像图像对电极属性敏感，如接触阻抗。在医疗应用中，接触阻抗的值会随着身体运动和研究区域而变化。另外，它对接触层的特性很敏感，因此在临床实验中缺乏边界特性可能导致不准确。在工程领域，与导电液体长时间接触后，电极的电化学腐蚀效应和极化效应可能会导致严重的误差，电极的污染可能会带来严重的测量偏差。2010年，王等人提出了一种称为电容耦合电阻层析成像(ccert)的非接触方法。基于电容耦合非接触电导率检测(c4d)技术，ccert通过在电极和导电液体之间插入绝缘层来避免接触误差。与其它电学层析成像技术一样，ccert也存在高度非线性和不适定的逆问题，阻碍了电学层析成像技术的发展。用于解决逆问题的传统算法包括非迭代方法和迭代方法，面临重建速度和精度的挑战。到目前为止，已经提出了许多方法用于ccert中的图像重建。如b l wang等人提出了一种结合tikhonov正则化和同步迭代重建技术的混合图像重建方法，引入tikhonov正则化获得初始重建图像，sirt用于获得最终的重建图像，用于恢复ccert中的电导率分布。w h tan等人是通过将levenberg-marquardt(l-m)方法与同步代数重建技术相结合来实现ccert的图像重建。以l-m方法得到的图像灰度分布为初始迭代值，采用同步代数重建技术实现重建。y x wang等人提出了一种将线性反投影算法和k均值聚类算法相结合的图像重建方法。利用线性反投影算法获得原始重建图像，利用k均值聚类算法获得灰度阈值，进而实现图像重建。值得注意的是，在ccert中对图像重建的研究很少。虽然已经获得了一些令人满意的结果，但是重建图像的空间分辨率仍然需要提高。目前解决不适定问题比较常用的方法是正则化方法，通过在目标函数中加入正则项的方法来稳定解。为了处理典型的不适定反问题，tikhonov正则化是一种经典的方法。通过添加平滑正则化项，不适定问题被正则化，然而，tikhonov正则化方法不能很好地保留图像的边缘，从而降低了重建图像的分辨率。与tikhonov正则化相比，全变分正则项的使用使得图像质量有了很大的改善，全变分的优势是在抑制重建图像噪声的同时，仍保留图像的边缘细节信息。然而，全变分正则化方法在重建图像的平滑区域时经常出现不想要的阶梯伪影，称为“阶梯效应”。为了抑制阶梯效应，提高图像的分辨率，本发明提
出了一种新型的电容耦合电阻层析成像图像重建方法，背景清晰，目标物重建准确，抗噪性能好。


技术实现要素：

3.本发明解决的技术问题是提供了一种电容耦合电阻层析成像图像重建方法，相比于全变分正则化方法，本发明所提出的新型的全变分正则化方法分辨率更高，背景更清晰，在去阶梯效应方面展现出了优越的性能，明显的抑制了重建图像的阶梯效应，而且在保证抑制阶梯效应效果的基础上，能够进一步增强对边缘信息的保留。
4.本发明的技术方案为：本发明提出了一种新型的全变分正则化算法来求解电容耦合电阻层析成像的逆问题，其最小化的目标函数为：其中，||
·
||为欧几里得范数，s代表灵敏度矩阵，它反映了在被测区域中由电导率变化引起的电阻变化，g表示电导率变化，h表示等效电阻的变化，d
p
表示p阶有限差分，d是离散梯度，是预测的最优电导率，λ是正则化参数，用于平衡保真度项和正则化项。
5.在目标函数中引入1个辅助变量w，目标函数还可以表示为：
[0006][0007]
由于上式的不可微性和非线性，仍然难以直接有效地求解，将上式表示为最小化增广拉格朗日函数：
[0008][0009]
式中，t表示矩阵的转置算子，v,β和μ是增广拉格朗日乘子。
[0010]
重建的算法包含以下步骤：(1)针对被测对象，获取重建所需的边界测量值和灵敏度矩阵：边界测量值是将被测对象置于电容耦合电阻层析成像测量系统中，被测场域外均匀分布12个电极，采用电压激励、电流测量的模式，采集单电极激励、单电极测量下的边界测量值，共获得132个边界测量值。(2)提出本发明的目标函数。(3)为了便于计算，引入1个辅助变量w，写出目标函数的最小化增广拉格朗日函数。(4)求解目标函数的算法，包括设置初始化参数，更新正则化参数λ，更新辅助变量w，更新电导率分布判断迭代是否符合迭代终止条件。(5)根据求解出的最优灰度值完成图像的重建。
[0011]
本发明与现有技术相比具有以下有益效果：本发明提出了一种新型的全变分正则化方法，用于实现电容耦合电阻层析成像图像的重建。本发明对这种新型的全变分正则化方法的性能进行了定性和定量分析。结果表明，所提出的新型的全变分正则化方法成像的质量更高，背景更清晰，在保证有效抑制阶梯效应的基础上，可以进一步地增强对重建图像边缘信息的保留。
附图说明
[0012]
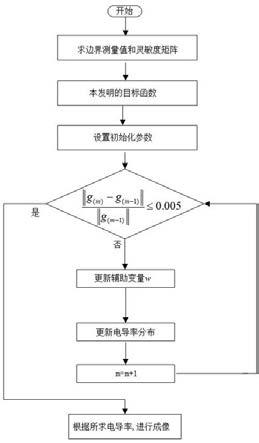
图1为本发明的新型的全变分正则化电容耦合电阻层析成像方法图像重建的流程框图；
[0013]
图2为本发明的电容耦合电阻层析成像传感器电极阵列图；
[0014]
图3为选取的三种经典模型在相同电导率下，分别通过landweber方法，newton-raphson方法，tikhonov方法和新型的全变分正则化电容耦合电阻层析成像方法图像重建的结果图；
[0015]
图4为四种方法在不同电导率下对模型重建的结果图；
[0016]
图5为三种经典模型在相同电导率下，通过四种方法进行重建时计算的模糊半径对比表；
[0017]
图6为三种经典模型在相同电导率下，通过四种方法进行重建时计算的时间对比表；
[0018]
图7为在相同电导率下，四种方法在1％噪声水平下对三种模型重建的结果图；
[0019]
图8为在不同电导率下，四种方法在1％噪声水平下对模型重建的结果图；
[0020]
图9为在相同电导率下，四种方法在1％噪声水平下，对三种模型重建时计算的模糊半径对比表。
具体实施方式
[0021]
结合附图详细对本发明的新型的全变分正则化电容耦合电阻层析成像方法加以说明。
[0022]
本发明的新型的全变分正则化电容耦合电阻层析成像方法，针对在利用全变分正则化方法重建图像时，产生的实时性不好问题与背景不清晰的问题。通过自适应的方法选择正则化参数，来去权衡保真度项与正则项之前的权重。
[0023]
如图1所示，为本发明的新型的全变分正则化电容耦合电阻层析成像方法图像重建的流程框图。
[0024]
如图2所示，为本发明的电容耦合电阻层析成像传感器电极阵列图，十二个电极等距离地安装在充满导电介质的绝缘管外部。选择一个电极由交流电压激励，一个电极作为测量端子，在两个电极之间建立交流路径，并采用电压激励、电流测量的模式，采集单电极激励、单电极测量下的边界测量值。最后，根据边界测量值重构内部电导率的分布情况。
[0025]
如图3所示，本发明选取了三种不同的模型进行电导率分布的重建，图中第一列为重建的真实模型，右边三列依次为landweber方法、newton-raphson方法、tikhonov方法和新型的全变分正则化电容耦合电阻层析成像方法重建的电导率分布的图像。结果表明，用landweber方法重建的图像质量最差，重建的内含物往往比原始物体大得多。对于在检测区域中存在多个内含物的模型，从重建图像中不能清楚地识别内含物的边界。而且由于这种方法是半收敛的，不一定能找到最优解，所以解不是很精确。与landweber方法相比，newton-raphson方法重建的图像普遍得到改善，边界更清晰，更容易识别内含物之间的边界。tikhonov方法重建的图像与newton-raphson方法的结果相似。然而，用tikhonov方法重建所需的时间要少得多，但是内含物仍未得到很好的重建，重建图像中存在明显的伪影。相比之下，用本发明的方法重建的图像得到了很大的改善。内含物是四种方法中重建最准确的。此外，内含物的边界最清晰，背景中几乎没有观察到伪影。
[0026]
电容耦合电阻层析成像图像重建是一个严重不适定性的逆问题。为了提高重建图像的质量，克服实时性不好问题与背景不清晰的问题。本发明提出了一种新型的全变分正则化电容耦合电阻层析成像方法，具体实施步骤如下：
[0027]
步骤一：针对被测对象，获取重建所需的边界测量值和灵敏度矩阵：边界测量值是将被测对象置于电容耦合电阻层析成像测量系统中，被测场域外均匀分布12个电极，采用电压激励、电流测量的模式，采集单电极激励、单电极测量下的边界测量值，共获得132个边界测量值；
[0028]
灵敏度矩阵是根据不含内含物的空场的边界测量值，结合灵敏度理论计算得到的，计算公式为：其中s
ij
是第j个电极对对第i个电极对的灵敏度系数，是所有元素电导率为σ0的第i个元素的电阻测量值，是第j个元素电导率从σ0变为σ1时第i个元素的电阻测量值；
[0029]
步骤二：为了便于计算，引入1个辅助变量w,目标函数还可以表示为：
[0030][0031]
由于上式的不可微性和非线性，仍然难以直接有效地求解，将上式表示为最小化增广拉格朗日函数：
[0032][0033]
式中，t表示矩阵的转置算子，v,β和μ是增广拉格朗日乘子。
[0034]
步骤三：求解目标函数算法如下：
[0035]
1)初始化：0＜δ,μ,η＜1,c0＝la(w0,g0)；
[0036]
2)更新辅助变量w:式中，m表示第m次迭代；
[0037]
3)更新电导率分布g
m+1
＝(β(d
p
)
tdp
+μs
t
s)
+
((d
p
)
t
v+β(d
p
)
twm+1
+s
t
λ+μs
t
h)
[0038]
为了提高计算效率和提高解的稳定性，采用一步最速下降法求解g
m+1
子问题
[0039]gm+1
＝g
m-α
mdm
，
[0040]
式中，步长d是目标函数的梯度方向，zm＝g
m-g
m-1
，ym＝dm(gm)-dm(g
m+1
)，
[0041]
当αm满足条件时，方可停止迭代，式中，p
m+1
＝ηpm+1；
[0042]
4)判断迭代是否符合迭代终止条件或者是否达到最大迭代次数，若是则迭代终止，进行下一步操作；若否，设置m＝m+1并跳回第3)步继续迭代求解。
[0043]
步骤四：根据最终求解出的最优灰度值完成图像的重建。
[0044]
如图4所示，四种方法在不同电导率下对模型重建的结果图，可以看出，本发明提出的新方法重建的图像明显优于其他三种正则化方法，内含物是最精确重建的，背景最清晰，没有观察到伪影。
[0045]
如图5所示，三种经典模型在相同电导率下，通过四种方法进行重建时计算的模糊半径对比表。模糊半径a
t
表示重建内含物的面积，a表示整个成像区域面积。br值体现了重建图像的精度，br值越小，表示成像目标越精确，伪影更少。在四种方法中，本发明提出的方法br值是最小的。
[0046]
如图6所示，三种经典模型在相同电导率下，通过四种方法进行重建时计算的时间对比表。在图像重建中，图像重建方法的计算时间也很重要。由于tikhonov方法不需要迭代，重建花费的时间最短，newton-raphson方法耗时最长，因为需要多次迭代。相比较而言，本发明的方法的计算时间仅仅长于tikhonov方法。
[0047]
如图7所示，在相同电导率下，四种方法在1％噪声水平下对三种模型重建的结果图。在四种方法中，本发明提出的方法对噪声的鲁棒性最强，内含物是重建最好的，背景显示最少的伪影。
[0048]
如图8所示，在不同电导率下，四种方法在1％噪声水平下对模型重建的结果图。用本发明提出的方法可以更好地重建内含物的形状，而且重建受噪声的影响较小。相比之下，其他三种方法的重建图像会产生严重的内含物变形和大量的伪影。
[0049]
如图9所示，为在相同电导率下，四种方法在1％噪声水平下，对三种模型重建时计算的模糊半径对比表，本发明提出的方法br值是最小的，进一步证明了该方法对噪声的鲁棒性。
[0050]
以上所述仅为本发明的较佳实施例而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。