1.本发明涉及柔性航天器的控制技术领域，具体涉及一种柔性航天器的姿态控制方法。


背景技术：

2.近半个世纪以来，柔性航天器在深空探测任务中发挥了巨大的优势。因此，航天器系统的姿态稳定问题具有重要的现实意义，受到了相当多的关注。与刚性航天器相比，柔性航天器在实现快速姿态机动方面具有一定的优势，并且服役年限较长。
3.然而，柔性部分在发射过程中会对航天器造成弹性振动。这可能会破坏航天器系统的稳定性和控制性能。此外，航天器系统还具有一些显著的特点:高非线性和强耦合。这些特性是姿态控制器设计中的难题。另外，在航天器执行任务过程中，不可避免地受到多种类型的干扰。所以，柔性航天器系统的姿态控制显然是一项具有挑战性的工作。


技术实现要素：

4.本发明的目的在于提供一种柔性航天器的姿态控制方法。
5.为实现上述目的，一方面，本发明提出了一种柔性航天器的姿态控制方法，包括：
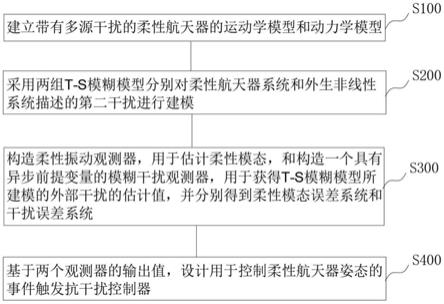
6.s100,建立带有多源干扰的柔性航天器的运动学模型和动力学模型，所述多源干扰包括属于l2空间的第一干扰和由外生非线性系统描述的第二干扰；
7.s200，采用两组t-s模糊模型分别对柔性航天器系统和外生非线性系统描述的第二干扰进行建模；
8.s300，构造柔性振动观测器，用于估计柔性模态，和构造一个具有异步前提变量的模糊干扰观测器，用于获得所述t-s模糊模型所建模的外部干扰的估计值，并分别得到柔性模态误差系统和干扰误差系统；
9.s400，基于两个观测器的输出值，设计用于控制柔性航天器姿态的事件触发抗干扰控制器。
10.在一优选实施例中，所述s100中，所述运动学模型为：
[0011][0012][0013]
其中，q0∈r,qv∈r3是四元数，其中满足i∈r3×3是单位矩阵，w(t)＝[w1,w2,w3]
t
∈r3代表角速度,q
×
是斜对称矩阵。
[0014]
在一优选实施例中，s100中，所述动力学模型表示为：
[0015]
[0016][0017]
其中，j∈r3×3，表示惯性矩阵,η(t)∈rr，表示柔性模态向量,δ∈r3×r，表示耦合矩阵,c＝diag{2ξkωk,k＝1,2,...，r}∈rr×r，表示阻尼矩阵,r表示模态数量,k＝diag{ω
k2
,k＝1,2,...，r}∈rr×r,表示刚度矩阵，ξk表示阻尼率,ωk表示频率,u(t)＝(u1,u2,u3)∈r3，表示控制力矩,d(t)＝(d1,d2,d3)∈r3，表示外生干扰，d0(t)∈l2(0，∞；rn)，表示第一干扰。
[0018]
在一优选实施例中，所述外生干扰d(t)由t-s模糊模型描述：
[0019][0020]
其中，常数矩阵wj∈rr×r，uj∈r3×r是已知的，υ(t)＝[υ1(t),...,υr]是状态变量,φ＝[φ1φ2…
φr]是前件变量，是模糊集合，是模糊集合，是规则数目，目，是隶属于的等级，oj(φ)≥0,
[0021]
在一优选实施例中，柔性航天器系统对应的模型表示为：
[0022][0023]
其中，对任意v，系统参数矩阵ai和b是：
[0024][0025]d1i
＝-s(x
ωi
(t)))δ
t
ψ+δ
t
(cψ+kη-cδω),是系统输出向量，ci∈r6×6是已知的。
[0026]
在一优选实施例中，所述s300中，所述柔性振动观测器表示为：
[0027][0028]
其中，
[0029]
在一优选实施例中，所述s300中，所述柔性模态误差系统表示为：
[0030][0031]
其中，
[0032]
在一优选实施例中，所述s300中，所述模糊干扰观测器表示为：
[0033][0034]
其中，ζ(t)是辅助变量,是υ(t)的估计，l是观测器的增益。
[0035]
在一优选实施例中，所述s300中，所述干扰误差系统表示为：
[0036][0037]
其中，
[0038]
在一优选实施例中，所述s400中，所述事件触发抗干扰控制器的控制规律为：
[0039][0040]
其中，uc(t)是基于观测器的模糊控制律,un(t)是补偿由事件触发引起的测量误差的非线性控制律，e(t)＝w(t)-u(t)代表由事件触发引起的测量误差,tk代表当前事件触发时刻，当触发条件被满足时,这个时刻被标记为t
k+1
,此时控制信号u(t
k+1
)作用于系统，在t∈[tk,t
k+1
),控制信号保持w(tk)。
[0041]
与现有技术相比，本发明具有如下有益效果：本发明建立带有多源干扰的柔性航天器的运动学模型和动力学模型，采用两组t-s模糊模型分别对柔性航天器系统和外生非线性系统进行建模，构造柔性振动观测器，用于估计柔性模态，和构造一个具有异步前提变量的模糊干扰观测器，用于获得t-s模糊模型所建模的外部干扰的估计值，并分别得到柔性模态误差系统和干扰误差系统，基于观测器的输出值，设计用于控制柔性航天器姿态的事件触发抗干扰控制器，保证了闭环系统的渐近稳定性，并严格满足耗散性能，节省了系统通信资源。本发明针对受到多源干扰的非线性柔性航天器系统，提供一种基于t-s模糊模型的耗散事件触发抗干扰控制方法，消减了柔性振动和外部干扰因素，实现振动抑制和姿态稳定，提高了系统抗干扰性能；同时设计事件触发机制，节约了通讯资源，适用于柔性航天器
的姿态控制。
附图说明：
[0042]
图1为本发明方法的流程示意图。
具体实施方式：
[0043]
下面对本发明的具体实施方式进行详细描述，但应当理解本发明的保护范围并不受具体实施方式的限制。
[0044]
除非另有其它明确表示，否则在整个说明书和权利要求书中，术语“包括”或其变换如“包含”或“包括有”等等将被理解为包括所陈述的元件或组成部分，而并未排除其它元件或其它组成部分。
[0045]
如图1所示，本发明所揭示的一种柔性航天器的姿态控制方法，包括以下步骤：
[0046]
s100,建立带有多源干扰的柔性航天器的运动学模型和动力学模型，所述多源干扰包括属于l2空间的第一干扰和外生非线性系统描述的第二干扰。
[0047]
具体地，在该步骤中，运动学模型具体为：
[0048][0049]
其中，q0∈r,qv∈r3是四元数，其中满足i∈r3×3是单位矩阵，w(t)＝[w1,w2,w3]
t
∈r3代表角速度,q
×
是斜对称矩阵。
[0050]
动力学模型具体为：
[0051][0052]
其中，j∈r3×3，表示惯性矩阵,η(t)∈rr，表示柔性模态向量,δ∈r3×r，表示耦合矩阵,c＝diag{2ξkωk,k＝1,2,...，r}∈rr×r，表示阻尼矩阵,r表示模态数量,k＝diag{ω
k2
,k＝1,2,...，r}∈rr×r,表示刚度矩阵，ξk表示阻尼率,ωk表示频率,u(t)＝(u1,u2,u3)∈r3，表示控制力矩,d(t)＝(d1,d2,d3)∈r3，表示外生非线性系统描述的第二干扰，d0(t)∈l2(0，∞；rn)，表示第二干扰。
[0053]
本实施例中，惯性矩阵耦合矩阵选择频率ω
n1
＝0.7681rad/s,ω
n2
＝0.7681rad/s,ω
n3
＝0.7681rad/s，相应的阻尼率是ξ1＝0.0056,ξ2＝0.0086,ξ3＝0.0013。c
＝diag{2ξkωk,k＝1,2,...，r}∈rr×r，k＝diag{ω
k2
,k＝1,2,
…
，r}∈rr×r，d0(t)＝0.2sin(5πt)e-0.2t
，ω(0)＝[0.1
ꢀ‑
0.3 0.2]
t
(rad/s),q0(0)＝0.755,qv(0)＝[0.3 0.5
ꢀ‑
0.3]
t
是状态变量的初始值。η(0)＝[-0.001 0.002 0.001]
t
,ψ(0)＝[0 0 0]
t
是柔性模态的初始值。
[0054]
s200，采用两组t-s模糊模型分别对柔性航天器系统和所述外生非线性系统进行建模。
[0055]
上述外生干扰d(t)由下述t-s模糊模型描述：
[0056]
规则j:如果φ1是φ2是
…
,φr是那么，
[0057][0058]
常数矩阵wj∈rr×r，uj∈r3×r是已知的，υ(t)＝[υ1(t),
…
,υr]是状态变量,φ＝[φ1φ2…
φr]是前件变量，是模糊集合，是规则数目。
[0059]
基于t-s模糊模型,外部干扰d(t)可以被描述为
[0060][0061][0061]
是隶属于的等级，oj(φ)≥0,对于任意φ,mj(φ)满足
[0062]
假设前件变量与υ(t)相关,干扰模型(1.20)被表示为：
[0063][0064]
其中，υ(0)＝[0.8 0.5]
t
。
[0065]
所建立的t-s模糊干扰模型适用于描述不同类型的干扰：
[0066]
情况一：首先考虑谐波干扰，给出相应的t-s模糊模型如下：
[0067]
模型1:
[0068]
规则1:如果υ1是那么d(t)＝v1υ(t)；
[0069]
规则2:如果υ1是那么d(t)＝v2υ(t)；
[0070]
规则3:如果υ1是那么d(t)＝v3υ(t)；
[0071]
规则4:如果υ1是那么d(t)＝v4υ(t)；
[0072]
规则5:如果υ1是那么d(t)＝v5υ(t)；
[0073]
规则6:如果υ1是那么d(t)＝v6υ(t)；
[0074]
规则7:如果υ1是那么d(t)＝v7υ(t)；
[0075]
其中：
[0076][0077][0078][0079]
选择隶属度函数如下:
[0080][0081][0082][0083]
情况二：考虑脉冲干扰的情况，系统矩阵如下所示：
[0084][0085][0086][0087]
相应的隶属度函数被选择为：
[0088][0089][0090][0091]
情况三：考虑不规则的干扰，系统矩阵如下所示：
[0092]
[0093][0094][0095]
选择模糊隶属度函数如下：
[0096][0097][0098][0099]
定义那么，系统(1.17)和可以转化为：
[0100][0101][0102][0103]
其中，j0＝j-δ
t
δ。
[0104]
建立t-s模糊模型：
[0105]
选择七个工作点：选择七个工作点：选择七个工作点：建立下列t-s模糊规则:
[0106][0107]
其中，ci(i∈s)＝0.01i6×6，
[0108][0109]
s300，构造柔性振动观测器，用于估计柔性模态，和构造一个具有异步前提变量的模糊干扰观测器，用于获得所述t-s模糊模型所建模的外部干扰的估计值，模糊干扰观测器的隶属函数不必与外部干扰的t-s模糊系统相同，并分别得到柔性模态误差系统和干扰误差系统。
[0110]
具体地，所述柔性振动观测器表示为：
[0111][0112]
其中，
[0113]
所述柔性模态误差系统表示为：
[0114][0115]
其中，
[0116]
构造模糊干扰观测器:
[0117][0118]
ζ(t)是辅助变量,是υ(t)的估计，l是观测器的增益。
[0119]
令可以得到干扰误差系统：
[0120][0121]
其中，
[0122]
s400，基于两个观测器的输出值，设计用于控制柔性航天器姿态的事件触发抗干扰控制器，并引进能量供给函数，使系统满足严格耗散性能。
[0123]
基于并联分布式补偿控制方法，设计一种耗散事件触发抗干扰模糊控制律，其中第l条规则如下：
[0124]
控制规则l:如果v1(t)是θ
l1
，
…
，v6(t)是θ
l6
,那么：
[0125]
w(t)＝u
cl
(t)+un(t),
[0126]
[0127]kl
∈r3×6,l＝1,2,
…
,λ,是控制器增益。如果v(t)由状态变量定义,系统的控制律如下：
[0128]
w(t)＝uc(t)+un(t)，
[0129][0130][0131][0132]
其中，uc(t)是基于观测器的模糊控制律，un(t)是补偿由事件触发引起的测量误差的非线性控制律。e(t)＝w(t)-u(t)代表由事件触发引起的测量误差，tk代表当前事件触发时刻，当触发条件被满足时，这个时刻被标记为t
k+1
，此时控制信号u(t
k+1
)作用于系统。在t∈[tk，t
k+1
)，控制信号保持w(tk)。
[0133]
设计un如下：
[0134][0135]
其中p1＞0是对称矩阵，
ò
＝0.2，ι1＝0.5。
[0136]
当t∈[tk，t
k+1
)，可以得到：
[0137]
w(t)＝(1+κ1(t)∈)u(t)+κ2(t)ι1，
[0138][0139]
其中κ1(t)，κ2(t)是满足|κ1|≤1，|κ2|≤1的变量。
[0140]
将代入得到：
[0141][0142]
当d0(t)出现时，在零初始状态下，闭环系统满足严格(q，s，r)-α-耗散性：
[0143][0144]
引进能量供给函数e(t)如下:
[0145][0146]
其中，α＝0.5,dq＝i3×3，r＝4.4i3×3。
[0147]
本发明的优点在于，本发明建立带有多源干扰的柔性航天器的运动学模型和动力
学模型，采用两组t-s模糊模型分别对柔性航天器系统和外生非线性系统进行建模，构造柔性振动观测器，用于估计柔性模态，和构造一个具有异步前提变量的模糊干扰观测器，用于获得t-s模糊模型所建模的外部干扰的估计值，并分别得到柔性模态误差系统和干扰误差系统，基于观测器的输出值，设计用于控制柔性航天器姿态的事件触发抗干扰控制器，保证了闭环系统的渐近稳定性，并严格满足耗散性能，节省了系统通信资源。本发明针对受到多源干扰的非线性柔性航天器系统，提供一种基于t-s模糊模型的耗散事件触发抗干扰控制方法，消减了柔性振动和外部干扰因素，实现振动抑制和姿态稳定，提高了系统抗干扰性能；同时设计事件触发机制，节约了通讯资源，适用于柔性航天器的姿态控制。
[0148]
需要说明的是，本发明说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。
[0149]
前述对本发明的具体示例性实施方案的描述是为了说明和例证的目的。这些描述并非想将本发明限定为所公开的精确形式，并且很显然，根据上述教导，可以进行很多改变和变化。对示例性实施例进行选择和描述的目的在于解释本发明的特定原理及其实际应用，从而使得本领域的技术人员能够实现并利用本发明的各种不同的示例性实施方案以及各种不同的选择和改变。本发明的范围意在由权利要求书及其等同形式所限定。