1.本发明涉及计算全息技术领域，具体涉及一种基于深度学习加速计算的大视场全息投影方法及系统。


背景技术：

2.全息投影本质上不需要透镜，可以减小光学系统的尺寸、重建高对比度的图像，还具有可用空间光调制器(spatiallightmodulator，slm)重建彩色图像的优点。衍射光学元件(diffractiveopticalelements,doe)是一种透射式的光相位调制器件，通过改变衍射光学元件平面的相位分布(即衍射光学元件的阶梯状面形)可以得到任意形状的衍射场图像。基于计算全息技术，传统的计算全息是将计算好的全息图加载到空间光调制器上而得到投影面上的图形。由于全息图的衍射过程可以用菲涅尔衍射来描述，菲涅尔衍射积分用于作为近轴近似解。常用的衍射数值计算算法是通过逆向的单次快速傅里叶变换算法(singlefastfouriertransformalgorithm,s-fft算法)来获得全息图，该算法适用于衍射距离较大的情况。为提高计算精度常使用盖师贝格-撒克斯通(gerchberg
–
saxton,g-s)算法：一次迭代使用正、逆单次快速傅里叶变换算法，多次迭代后可以得到质量更好的全息图。但是盖师贝格-撒克斯通算法有两个明显缺点：1、计算过程耗时久；2、在单次快速傅里叶变换算法中，投影面采样间隔存在以下局限性：
3.δx＝λd/nδx0(1)
4.其中δx是投影表面的采样间隔，λ是波长，d是衍射距离，n是取样数，δx0是全息图的采样间隔。因此，在实际的实验系统中难以获得较大的投影图像，限制了全息投影的应用范围。
5.为了进一步增加投影系统的视角，采用发散球面波照射空间光调制器较为有效，并有了相应的双采样算法(double-samplingfresnel,dsf)。由于双采样算法耗时较长，无法在实时投影系统中使用。
6.现有的大视场全息投影系统实时响应慢、成像质量不高。目前的无透镜投影系统的原理基于计算全息技术使用迭代算法来计算调制面的全息图，时间消耗较大，难以实现实时的投影图案变换。


技术实现要素：

7.本发明提出一种基于深度学习加速计算的大视场全息投影方法及系统，可解决传统方法耗时久的问题，实现实时的投影图案变换。
8.本发明为达上述目的所提出的技术方案如下：
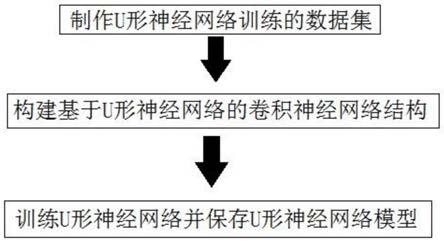
9.基于深度学习加速计算的大视场全息投影方法，包括如下步骤：
10.s1、通过盖师贝格-撒克斯通算法计算无透镜投影系统中生成的全息图，制作u形神经网络训练的数据集；
11.s2、构建基于u形神经网络的卷积神经网络结构；
12.s3、将所述数据集输入所述u形神经网络进行训练并保存训练得到的u形 神经网络模型。
13.进一步地：
14.步骤s1中，所述无透镜投影系统包括激光器，显微物镜，针孔，数字微镜 器件，tir棱镜，衍射光学元件和投影面；
15.所述激光器、显微物镜、针孔依次机械连接，光路保持共轴，所述tir棱 镜用于接收所述针孔发出的发散的球面波并将其发射到到所述数字微镜器件上， 所述数字微镜器件与所述针孔处点光源的最小距离是80mm，所述数字微镜器件 平面与所述衍射光学元件平面距离为400mm，所述投影面用于接收所述衍射光 学元件发射过来的球面波并显示图像；
16.所述激光器发出的激光经过所述显微物镜和所述针孔后成为发散的球面波；
17.所述球面波依次经过数字微镜器件的振幅调制、衍射光学元件的相位调制， 实时地在投影处产生图像。
18.进一步地：
19.所述无透镜投影系统包括依次经过所述数字微镜器件平面、所述衍射光学元 件平面、所述投影面的正向衍射过程：
20.所述衍射过程为菲涅尔衍射，衍射场的精确解可根据以下公式计算得到：
[0021][0022][0023]
其中x和y分别表示成像平面内两个垂直方向坐标，u(x,y)表示投影面的复 振幅分布，u1(x1,y1)表示数字微镜器件面的复振幅分布，exp是以自然常数e为 底的指数函数，i为虚数，d是衍射距离，a表示振幅，φ
doe
表示衍射光学元件上 的相位，δx是投影面上的采样间距，δx1是数字微镜器件平面上的采样间距，δx2是衍射光学元件平面上的采样间距，sasm表示角谱法，k为传播常数。
[0024]
进一步地：
[0025]
所述无透镜投影系统还包括依次经过所述投影面、所述衍射光学元件平面、 所述数字微镜器件平面的逆向衍射过程：
[0026]
所述逆向衍射过程为夫琅禾费衍射，衍射场的精确解根据以下公式计算：
[0027]
u1(x1,y1)＝sasm-1
[d2,δx,δx2]
×at exp(iφu)
×
sasm-1
[d1,δx2,δx1]
×
exp(-iφ
doe
)
[0028]
所述投影面的采样间隔δx应根据以下公式计算：
[0029]
δx＝λd/nδx0[0030]
其中λ是波长，d是衍射距离，n是取样数，δx0是全息图的采样间隔。
[0031]
进一步地：
[0032]
所述盖师贝格-撒克斯通算法的具体流程包括：
[0033]
s1-1、对初始相位和事先给定的入射光场分布进行所述正向衍射的变换，得 到目标平面光场分布；
[0034]
s1-2、在目标平面上引入约束，即在保持相位分布不变的同时用所需目标平 面光
场的振幅分布替换所述正向衍射计算后的目标面光场的振幅分布；
[0035]
s1-3、执行所述逆向衍射的变换以获得衍射面的光场分布；
[0036]
s1-4、在衍射面引入约束，即用给定的入射光场振幅分布替换所述逆向衍射 得到的光场振幅分布，同时保持相位不变，由此得到经过一次迭代后的值，同时 将其作为下一次迭代的初始分布；
[0037]
s1-5、再次进行所述正向衍射的变换，并继续断迭代循环直到迭代精度达到 事先设定的迭代退出条件：迭代的结果达到设定的精度或者达到最大迭代次数， 最后获得全息面上的振幅全息图。
[0038]
进一步地：
[0039]
步骤1中所述数据集包括训练集和测试集。
[0040]
进一步地：
[0041]
步骤s2中，所述u形神经网络的原理包括：经过一次所述降采样后，图像 的长度和宽度将减少一半，经过四次所述降采样处理即可实现输入图像的几何特 征提取；经过四次所述上采样过程后，将还原解码得到重构的原始大小图像输出； 为了避免梯度在网络训练过程中消失，增加了残差连接来实现梯度的跨层传递； 每次卷积后进行批处理归一化，避免过拟合。
[0042]
进一步地：
[0043]
所述u形神经网络是用tensorflow来编程实现卷积网络的，具体过程包括：
[0044]
s2-1、定义卷积层，继承于keras中的layer类的python类，包括：
[0045]
s2-1-1、用初始化函数__init__初始化参数：卷积核数量、卷积核大小、训 练状态、采样状态(上采样或是下采样)、是否使用bn算法；
[0046]
s2-1-2、使用构建函数build表示具体的卷积操作(同步卷积、下采样卷积、 反卷积)和bn算法；
[0047]
s2-1-3、使用call函数描述一个卷积层中若干卷积操作之间的执行关系；
[0048]
s2-2、定义模型类，继承于keras中的model类，包括：
[0049]
s2-2-1、使用__init__函数完成u形神经网络模型的构建；
[0050]
s2-2-2、使用call函数则描述了图片张量在u形神经网络模型中的流动过程。
[0051]
进一步地：
[0052]
步骤3中所述u形神经网络训练的过程如下：
[0053]
s3-1、将所述训练集的图片作为输入图像，用盖师贝格-撒克斯通算法在全 息面上计算出的振幅全息图作为输出图像；
[0054]
s3-2、用均方根误差作为损失函数，初始学习率为l，每次训练使用16张 图像；
[0055]
s3-3、当均方根误差不再持续下降时，降低学习率，当学习率变为l/100时， 训练停止。
[0056]
本发明还提出一种基于深度学习加速计算的大视场全息投影系统，包括处理 器、存储器及存储在所述存储器上并可在所述处理器上运行的计算机程序，所述 计算机程序被所述处理器执行时实现如权利要求1-9任一项所述的方法。
[0057]
本发明具有如下有益效果：
[0058]
本发明提供一种基于深度学习加速计算的大视场全息投影方法及系统，将深 度
学习应用于计算全息领域，实现了物体相位和幅度的快速恢复，由于u形神 经网络(u-net)的输入和输出都是二维图片，并且在显卡的并行计算的帮助下， 卷积神经网络(convolutional neural networks,cnn)计算速度快，解决了传统迭 代算法收敛速度慢等问题，提高神经网络成像的质量，计算的全息图具有良好的 性能，实现了动态实时投影，并且具有一定的泛用性。
附图说明
[0059]
图1是本发明实施例的无透镜投影系统的光路示意图；
[0060]
图2是本发明实施例在无透镜投影系统中投影简单的几何图形示意图；
[0061]
图3是本发明实施例中盖师贝格-撒克斯通算法的具体流程图；
[0062]
图4是本发明实施例中u形神经网络的原理示意图；
[0063]
图5是本发明实施例中相关系数的散点图；
[0064]
图6a-6f是本发明实施例在投影面上获得的目标图像示意图；
[0065]
图7是本发明实施例中一种无透镜投影实验系统的光路示意图；图8是本发明实施例基于深度学习加速计算的大视场全息投影方法流程图。
具体实施方式
[0066]
以下对本发明的实施方式作详细说明。应该强调的是，下述说明仅仅是示例 性的，而不是为了限制本发明的范围及其应用。
[0067]
需要说明的是，术语“第一”、“第二”、“左”、“右”、“前”、“后
”ꢀ
仅用于描述目的，而不能理解为指示或暗示相对重要性或者隐含指明所指示的技 术特征的数量。由此，限定有“第一”、“第二”、“左”、“右”、“前”、
ꢀ“
后”的特征可以明示或者隐含地包括一个或者更多该特征。
[0068]
本发明中，菲涅尔衍射、角谱法和神经网络是关键技术。针对传统的全息投 影技术存在的迭代算法的时间消耗问题，在显卡并行计算的帮助下，利用了神经 网络高效率的特性。本发明在原有的正逆向盖师贝格-撒克斯通算法的基础上增 加了计算机深度学习，通过适宜的网络训练，达到了匀光效果，提升了成像性能。
[0069]
本发明使用盖师贝格-撒克斯通算法建立一个用于u形神经网络训练的数据 集，用该数据集训练u形神经网络，从而实现了一个能够快速改变投影模式的 大视场投影系统。经过训练，使用相关系数r对u形神经网络的计算结果进行 评估，结果表明，u形神经网络的训练结果与盖师贝格-撒克斯通算法得到的结 果十分相似。通过将y
net
和y
gs
加载到数字微镜器件(digital micromirror device， dmd)上，仿真表明：通过u形神经网络获得的全息图像可以使投影面呈现目标 图像，且u形神经网络计算生成全息的时间短。
[0070]
本发明实施例提供一种基于深度学习加速计算的大视场全息投影方法，该方 法主要包括以下三部分：
[0071]
一、u形神经网络训练的数据集准备
[0072]
本小节主要内容是制作u形神经网络训练数据的训练集和测试集。
[0073]
一种无透镜投影系统，其光路如图1所示，由红光激光器1发出的激光光束 被显微物镜2汇聚后又经过小孔滤波得到发散的球面波；球面波依次经过数字微 镜器件4的振幅
调制和衍射光学元件5的相位调制最终到达投影面6；在投影面 6成像出想要的目标投影图案。在此光学系统中，衍射光学元件5的作用是匀化 投影图案，数字微镜器件4作为全息面，是主要的成像器件。
[0074]
第一步，从数字微镜器件4平面到投影面6，正逆衍射场的精确解可根据以 下公式(2)计算得到：
[0075][0076]
u1(x1,y1)＝sasm-1
[d2,δx,δx2]
×
at
e xp(iφu)
×
sasm-1
[d1,δx2,δx1]
×
exp(-iφ
doe
)
ꢀꢀ
(3)
[0077][0078]
其中公式(2)为正向衍射过程，公式(3)为逆向衍射过程，x和y分别表示成像 平面内两个垂直方向坐标，u(x,y)表示投影面6的复振幅分布，u1(x1)表示数字 微镜器件4平面的复振幅分布，exp是以自然常数e为底的指数函数，i为虚数， k为波数，d是衍射距离，a表示振幅，φ
doe
表示衍射光学元件5上的相位，δx 是投影面6上的采样间距，δx1是数字微镜器件4平面上的采样间距，δx2是衍射 光学元件5平面上的采样间距，sasm表示角谱法，经过衍射光学元件5平面后 球面波的相位会发生变化。
[0079]
从点光源3平面到投影面6的过程为两次菲涅尔衍射，数字微镜器件4对发 散球面波的振幅进行调制，从而在投影面6得到目标图案。衍射光学元件5对球 面波的相位进行调制，使投影面6处的光场相位一样，达到匀光的效果。
[0080]
第二步，从投影面6回到数字微镜器件4平面，此过程为逆向的夫琅禾费衍 射，衍射场的精确解可根据公式(3)计算得出。这里的每个步骤都需要使用单次 快速傅里叶变换算法进行计算，因此采样间隔应根据公式(1)计算。因为全息面 的大小和投影表面上的采样间隔具有正相关关系，所以正向衍射过程为：
[0081][0082][0083]
在进行u形神经网络的训练前，需要准备数据集，对于无透镜投影系统而 言，先考虑投影简单的几何图形。为了获得卷积神经网络训练的数据集，可以通 过该卷积神经网络的规则生成投影面6上的图像，如图2所示，将分辨率为256
ꢀ×
256的正方形分为四个小的方形区域：aeoh、ebfo、ofcg和hogd。每 个小方形都可以沿着对角线进一步分成两个三角形。三角形可以是黑色也可以是 白色，所以小正方形有6种类型，由排列组合原理在投影面6上可得到1296幅 图像。
[0084]
数字微镜器件4平面的振幅和投影面6的相位是未知的，因此用正逆向盖师 贝格-撒克斯通算法对数字微镜器件4上的全息图进行计算。因为卷积神经网络 模式的本质特征是图像特征提取器，为了使加载在全息面和投影面6上的图案有 近似的图像特征，需要在全息面上加载振幅全息图。选用数字微镜器件4来作空 间光调制器，盖师贝格-撒克斯通算
法的具体流程如图3所示，首先对初始相位 和事先给定的入射光场分布进行正向衍射的变换，得到目标平面光场分布；然后 在目标平面上引入约束，即在保持相位分布不变的同时用所需目标平面光场的振 幅分布替换正向衍射计算后的目标面光场的振幅分布，然后执行逆向衍射的变换 以获得衍射面的光场分布；在衍射面引入约束，即用给定的入射光场振幅分布替 换逆向衍射得到的光场振幅分布，同时保持相位不变；由此得到经过一次迭代后 的值，同时将其作为下一次迭代的初始分布。然后再次进行正向衍射的变换，并 继续断迭代循环直到迭代精度达到事先设定的迭代退出条件：迭代的结果达到设 定的精度或者达到最大迭代次数，最后获得全息面上的振幅全息图。按照该盖师 贝格-撒克斯通算法的一系列步骤可获得1296组图片组成的数据集，其中1024 组图片作为训练集，272组图片作为测试集。
[0085]
对于相同的计算问题，衍射的角谱传递函数通常比其他传递函数更有效。从 采样次数和计算时间可以证实角谱传递函数的计算结果与菲涅尔衍射的计算结 果基本一致，理论上可以得到衍射问题的精确解。因此，在实际应用中使用角谱 衍射公式能够得到更可靠的结果。
[0086]
基于角谱衍射理论，将衍射场的精确解用傅里叶变换形式表示为：
[0087]
u(r2)＝f-1
[r2,f1]h(f1)f[f1,r1]{u(r1)}
ꢀꢀ
(5)
[0088]
其中r1是源平面坐标，r2是观察面坐标，h(f1)为自由空间传播的传递函数。
[0089][0090]
其中i是虚数，f
x1
指的是数字微镜器件4平面上x方向的采样频率，f
y1
是数 字微镜器件4平面上y方向的采样频率，δz是数字微镜器件4平面到衍射光学 元件5平面之间的距离。公式(5)是菲涅尔衍射积分的角频谱形式，用于菲涅 尔积分的数值求解。
[0091]
引入从源平面到观察平面的比例缩放参数m，
[0092][0093][0094]
带回式(7)，得到
[0095][0096]
定义缩放的坐标和距离：
[0097][0098][0099]
得到卷积形式的积分
[0100]
[0101]
其中：
[0102][0103][0104]
光的衍射是波光场角谱衍射的叠加，随着衍射距离的增大，衍射场范围呈线 性扩大当衍射距离较大时，卷积算法不能完全获得衍射场。因此，该角谱缩放算 法主要用于物波光场的高频角谱小，衍射距离小的情况。计算全息面上的振幅全 息图的仿真参数如表1所示。
[0105]
表1
[0106][0107]
二、设计一种基于残差u形神经网络的端到端卷积神经网络结构
[0108]
本小节主要内容是用tensorflow来构造u形神经网络。
[0109]
u形神经网络的原理如图4所示，矩形条表示卷积后的图像，图像的通道数 标记在矩形条附近。指向右的细箭头表示步长为1、卷积核大小为3
×
3的卷积 过程，向下的箭头表示步长为2、卷积核大小为3
×
3的卷积过程(降采样部分)， 向上的箭头表示反卷积过程(上采样部分)，向右的粗体箭头表示残差连接。每 次降采样后，图像的长度和宽度将减少一半，经过4次降采样处理即可实现输入 图像的几何特征提取。降采样用来减少过拟合的风险，降低运算量。经过4次上 采样过程后，将还原解码得到重构的原始大小图像输出。为了避免梯度在网络训 练过程中消失，增加了残差连接来实现梯度的跨层传递。每次卷积后进行批处理 归一化，避免过拟合。
[0110]
在用tensorflow来编程实现卷积网络时，首先定义卷积层： class down_or_up(tf.keras.layers.layer):
[0111]
def__init__(self,filter_num,kernel_len,istraining,downorup,usebn):
[0112]
……
[0113]
defbuild(self,input_shape):
[0114]
……
[0115]
defcall(self,inputs):
[0116]
……
[0117]
该python类继承于keras中的layer类，需要使用初始化函数__init__初始 化参数：卷积核数量、卷积核大小、训练状态、采样状态(上采样或是下采样)、 是否使用bn算法。
接着使用构建函数build表示具体的卷积操作(同步卷积、 下采样卷积、反卷积)和bn算法。最后使用call函数描述一个卷积层中若干卷 积操作之间的执行关系。
[0118]
接下来定义模型类，继承于keras中的model类：
[0119]
class unet(tf.keras.model):
[0120]
def__init__(self):
[0121]
……
[0122]
defcall(self,inputs):
[0123]
……
[0124]
其中__init__函数中完成了u形神经网络模型的构建。call函数则描述了图 片张量在u形神经网络模型中的流动过程。
[0125]
三、训练u形神经网络并保存u形神经网络模型
[0126]
本小节主要内容是对u形神经网络进行训练并评价u形神经网络训练后的 拟合效果。
[0127]
u形神经网络训练的具体过程如下：
[0128]
将投影面6上的图像作为输入图像，用盖师贝格-撒克斯通算法在全息面上 计算出的振幅全息图作为输出图像。然后用均方根误差(rmse)作为损失函数， 损失函数越小，网络模型的鲁棒性就越好。初始学习率为l，每次训练使用16 张图像。当均方根误差不再持续下降时，降低学习率，当学习率变为l/100时， 训练停止。训练结束时，均方根误差与256(灰度图像的取值范围)相比已经足够 小。
[0129]
将不同的训练集图片输入到u形神经网络进行反复训练，并使用测试集图 片来评价u形神经网络训练的拟合效果，计算u形神经网络输出y
net
与测试集的 理想输出y
label
间的相关系数r，用r来定量评估u形神经网络的计算结果。
[0130][0131]
其中y
net
是通过u形神经网络计算的振幅全息图，y
gs
是通过盖师贝格-撒克 斯通算法获得的振幅全息图，σ(y
net
)和σ(y
label
)为标准差，n为一张图片的总像 素数。和是平均值。当|r|的值接近1，即y
net
和y
gs
越相似，两张图片的 相似性越高。图5是相关系数的散点图，横坐标的数值代表图片序号，纵坐标的 数值代表相关系数r的绝对值，可见大多数r值大于0.9，说明u形神经网络的 结果与盖师贝格-撒克斯通算法计算的结果相似度很高，并且使用网络来加速全 息图计算是可行的。
[0132]
把y
gs
和y
net
加载到数字微镜器件4上后，将在投影面6上获得目标图像。 实验的进行分为两组，当y
gs
和y
net
分别加载到数字微镜器件4上时，图6(a)为 目标图像一，(b)是实验中从y
gs
获得它的投影，(c)是实验中由y
net
获得的投影； 图6(d)为目标图像二，(e)是实验中从y
gs
获得它的投影,(f)是实验中从y
net
获得的 投影，可以看到，图6(b)和(c)、(e)和(f)都十分接近各自的目标图像。
[0133]
计算i
gs
实验结果与i
unet
实验结果间的相关系数，两个图形的相关系数分别 是0.9244，0.9142。因此用合适的数据集训练得到的u形神经网络能够较好的代 替盖师贝格-撒克斯通算法和缩放角谱法来计算数字微镜器件4平面的振幅分布， 计算耗时仅是迭代算法的十分之一。
[0134]
本发明实施例还提供一种无透镜投影实验系统，该系统的光路如图7所示， 包括红色激光器1，显微物镜2，针孔7，数字微镜器件4，tir棱镜8，衍射光 学元件5和投影面6，红色激光器1发出的激光光束被显微物镜2汇聚后又经过 小孔滤波得到发散的球面波，球面波依次经过数字微镜器件4的振幅调制、加工 好的衍射光学元件5的相位调制，发散球面波实时地在投影处产生图像。为得到 尽可能大的视场角，在实验装置不产生机械干涉的情况下，所能达到的数字微镜 器件4与针孔7处点光源3的最小距离是80mm；又为了在衍射光学元件5平面 处尽可能的减少次级衍射的干扰，选择数字微镜器件4平面与衍射光学元件5 平面距离为400mm。优选的，采用波长为660nm的激光；数字微镜器件4采用dlp6500。
[0135]
具体地，该无透镜投影实验系统还包括软件设备：win10专业版64位； pycharm(integrated development environment，ide)，2019.2.3(community edition)； python 3.6.9；tensorflow-gpu 1.14；keras 2.2.5；matlab 2017a。
[0136]
本发明的背景部分可以包含关于本发明的问题或环境的背景信息，而不一定 是描述现有技术。因此，在背景技术部分中包含的内容并不是申请人对现有技术 的承认。
[0137]
以上内容是结合具体的优选实施方式对本发明所做的进一步详细说明，不能 认定本发明的具体实施只局限于这些说明。对于本发明所属技术领域的技术人员 来说，在不脱离本发明构思的前提下，还可以做出若干等同替代或明显变型，而 且性能或用途相同，都应当视为属于本发明的保护范围。