1.本发明涉及道路工程领域中的路面破损检测方法，具体涉及一种基于外摆线模型的路面破损检测方法。


背景技术：

2.在交通运输飞速发展的今天，过多的交通量在带来繁荣的同时，也为运输道路带来了极大的挑战。在大量的运输荷载下，道路路面也时常出现开裂、滑移、沉陷等问题。因此，运输道路在建成后的养护一直是关键所在，而这也对道路路面的检测方法提出了要求。
3.目前，人工检测的方法最为普遍却也最为浪费与耗时，故出于效率与人力的考虑，利用激光检测、图像识别、声波检测等技术进行路面破损检测也逐渐成为主流的识别检测方法。但这些方法常过于复杂，所需的数据也常难以采集与处理，且需要较高的实践成本，激光检测最为精准但是设备成本与操作要求往往过高，图像识别技术虽然足够先进。但也存在着受限于数据处理技术，图像分析手段的种种问题，声波检测的手段则也存在着传输介质与传导效率的实际困扰，这些种种方法，与人工的测量相比，无疑更加先进与快捷，更加准确与效率，但是却也存在着这样那样的问题。故亟需一种更加科学与准确的测量方法，有效的化解目前的种种困境。


技术实现要素：

4.发明目的：本发明的目的在于提出一种更为简洁方便的基于外摆线模型的路面破损检测方法，以实现对路面破损的更方便的检测，乃至于辅助修理。
5.技术方案：本发明提供一种基于外摆线模型的路面破损检测方法，具体包括以下步骤：
6.(1)构建外摆线模型；
7.(2)标准外摆线模型中圆o完成“一拱”所行进的路线为l0，圆上点r的运动轨迹为a0；
8.(3)对于存在破损的待测路路段，将圆o的运动路线记为l1，l1上r的外摆线轨迹为a1；
9.(4)在同一角度ti下，比较a1中与a0中r点空间位置(x
a1
，y
a1
)与(x
a0
，y
a0
)中的数据不同点，将不同点记为破损点bi；并记下此时圆o的转动角度ti，其中，i为正整数；
10.(5)计算出所有的破损点bi与原点的距离位置，并标注于l1上；并将a0的高程数据与a1的高程数据进行对比；
11.(6)在剩余破损路面上重新选择路线，记为l2，重复上述步骤(3)-(5)，直至将所有路面区域测完。
12.进一步地，步骤(1)所述外摆线模型构建过程如下：
13.设一圆o，r为圆o的半径，t为圆o运动时半径所扫过的角度；r为圆上点，圆o沿直线l0朝着固定方向滚动其周长的距离时，其上的点r在这过程中运动出一段轨迹a0，称为“一
拱”；圆o与圆o上点r的位置关系为标准外摆线模型；
14.以点r的初始位置为原点，l0为x轴，建立平面直角坐标系，对于其所划过的轨迹a0的数学表达，a0上各点的坐标(x
a0
，y
a0
)使用参数方程的方式表达为：
[0015][0016]
其中，x
a0 y
a0
为圆o滚动一个周长，自转角度从0转到2π过程，圆上点r在运动“一拱”的空间位置；r为圆o的半径，t为圆o的自转角度，t的范围在[0：2π]之间。
[0017]
进一步地，步骤(2)所述的a0的上的点的坐标x
a0
，y
a0
之间的关系为：
[0018][0019]
点r的坐标(x
a0
，y
a0
)是仅与圆o的半径，以及与圆转过的角度t有关，而与其他因素无关。
[0020]
进一步地，步骤(5)所述的破损特异点bi与原点的距离为：
[0021]
di＝ti
×rꢀꢀ
(3)
[0022]
其中，di为破损点bi与原点的距离，ti为该破损处对应圆o的转动角度值t，i为正整数。
[0023]
进一步地，步骤(5)所述的a0的高程数据与a1的高程数据进行对比过程如下：
[0024]
a1高程与a0高程相减得出破损处的高程差：
[0025]
δy＝破损路面高程-无破损路面高程＝y
a1-y
a0
；
[0026]
其中，δy为负值则代表破损路面高程低于无损路面高程；δy为正值则代表破损路面高程高于无损路面高程；a0高程指l0上的点r所运动过的轨迹a0上各点对水平地面的海拔高度；a1高程指l1上的点r所运动过的轨迹a0上各点对水平地面的海报高度。
[0027]
有益效果：与现有技术相比，本发明的有益效果：本发明从经典的外摆线模型出发，提出了一种新的计算路面破损的思路与方法，通过实际测量与科学计算两者的相辅相成，可以更加准确的测量出路面的破损状况，相比传统的计算方法，更加具有操作性，也更具有实用意义。
附图说明
[0028]
图1为本发明路面无破损时的外摆线模型示意图；
[0029]
图2为本发明实施例中破损路段示意图；
[0030]
图3本发明针对该实施例的数据模型图；
[0031]
图4为本发明路面破损状态下的外摆线模型示意图；
[0032]
图5为本发明实施例中路面破损检测方法的示意图；
[0033]
图6为采用本发明路面破损检测方法的最终结果示意图。
具体实施方式
[0034]
下面结合附图对本发明作进一步详细说明。
[0035]
本发明提出一种基于外摆线模型的路面破损检测方法，如图1所示，设存在一圆o，r为圆o的半径，t为圆o运动时半径所扫过的角度。存在圆上点r，圆o沿直线l0朝着固定方向
滚动其周长的距离时，其上的点r在这过程中运动出一段轨迹a0，这一标准轨迹的长度，被称为“一拱”。
[0036]
以点r的初始位置为原点，l0为x轴，建立平面直角坐标系，对于其所划过的轨迹a0的数学表达，a0上各点的坐标(x
a0
，y
a0
)使用参数方程的方式表达为：
[0037][0038]
其中，x
a0 y
a0
为圆o滚动一个周长，自转角度从0转到2π过程，圆上点r在运动“一拱”的空间位置；r为圆o的半径，t为圆o的自转角度，t的范围在[0：2π]之间。
[0039]
通过消参的方法，得到x
a0 y
a0
间的关系如下：
[0040][0041]
从上述公式(1)和公式(2)中可见，点r的坐标(x
a0
，y
a0
)是仅与圆o的半径，以及与圆转过的角度t有关，而与其他因素无关。
[0042]
当圆在水平面沿直线运行“一拱”时，点r的运动轨迹总会如上述的公式所描述的一样。本发明中这样的圆o与圆o上点r的位置关系为标准外摆线模型。而当路段出现破损时，对于破损处，其纵断面线形视为特殊的折线或曲线，圆o在这样的路线上滚动时，会出现不同于外摆线模型的r的运动轨迹，即r的空间位置(x
a0
，y
a0
)发生的改变，通过比对前后数据差异，而便据此判断在路面何处出现了破损。
[0043]
如图2所示，为本发明实施例中一处待测的存在破损的路段1，经过测量，该破损的路段长度为2.2m，宽为1.7m；并在该路段中心处存在不规则的路面破损，该破损长度为83cm，宽度为62cm，并分布有1.8cm～2.2cm的凹陷，对于此路面采用本发明的路面破损方法进行测量。
[0044]
如图3所示，在待测路段1上存在的路面未破损处，选取一条路线，记做l0，并将l0作为x轴。同时，在破损处选取另外一条路线，记做l1，则在路段无破损的情况下，存在如图1的外摆线模型r点运动轨迹情形。即，对于未破损的水平路面路线l0，将圆o未滚动时与地面的唯一接触点，定义为点r的初始位置，即原点；该原点在直角坐标系中的位置即为(0,0)。
[0045]
而当在破损的路面上所选取的l1上，圆o运行时，则有如图4的轨迹情形。此时，在破损的路线l1上的运行出点r的轨迹为a1，且a1的规律同样符合公式(1)与公式(2)。本发明通过对比a1与a0轨迹的差别，即图4中所标注的破损的路面中破损点bi与点r的初始原点距离坐标di的计算方法如下面公式(3)所示，进而知晓在di处存在着路面破损：
[0046]
di＝ti
×rꢀꢀ
(3)
[0047]
其中，di为破损点bi与点r的初始原点的距离坐标；ti为该破损处对应圆o的转动角度值，以弧度制表示，i为正整数。
[0048]
对图2中的路面，在待测路段未破损处，选取第一路线l0，并将l0作为x轴；选择半径为50cm的圆形实物o作为测量工具，使该圆形实物o在路线l0上滚动，然后通过公式(1)进行计算，其中r是圆形实物o的半径，本实施例中r＝50cm；t是圆形实物o滚动的角度，本实施例中t的间隔为0.1弧度，通过公式(1)计算得出45组a0的轨迹数据a0的高程数据y
a0
；具体如表1所示。
[0049]
在可能存在的破损路段选出一条路线，记为l1，做测量与计算，选择半径为50cm的圆形实物o作为测量工具，使该圆形实物o在路线l1上滚动，并且每隔5cm，即每转动5.72度做一次记录，记录下a1的轨迹数据，本实施例中，也记录45组数据；该数据包括圆o的滚动角度ti和a1高程数据y
a1
，具体如表1所示。
[0050]
通过对a0与a1的轨迹数据进行对比后发现，在45组数据中，轨迹a0与轨迹a1的不同数据有16组，记录下这16组数据所对应的角度值ti。
[0051]
如图5所示，通过发现的16组异常数据，即b1～b16所对应的16组数据ti角度t1～t16，利用公式(3)，计算出在路线l1上，获取的45个记录点中，存在的16组异常数据；表明在2.2m的路段上，在距离r的起始原点为d1～d16的距离的路面上存在着破损；将这些数据标注在l1上。
[0052]
如图6所示，接着重新在破损路面上选取除了l1之外的新路线，记作为l2、l3、l4、l5
……
路线，其中，如果路线上不存在破损的情况，则其上圆o的点r的运动轨迹将与标准外摆线模型中的一致，即与l0上的a0数据一致；而当各个路线上存在破损时，则如l1一样在距离r的起始原点为d1～d16的距离的路面上存在破损。
[0053]
将每条路线上存在破损的点标注在对应的路线li上，并将a0的高程数据与a1的高程数据进行对比，具体如表1所示。
[0054]
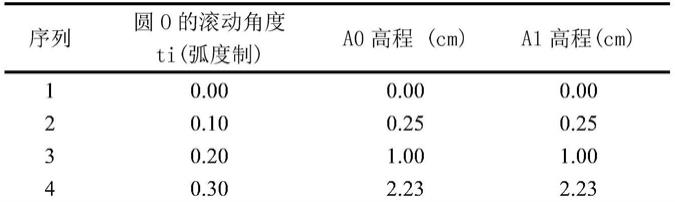
表1 ao高程数据与a1高程数据汇总
[0055]
[0056][0057]
a0高程指l0上的点r所运动过的轨迹a0上各点对水平地面的海拔高度；a1高程指l1上的点r所运动过的轨迹a0上各点对水平地面的海报高度，将每条路线上的a1高程与l0上的a0高程相减得出破损处的高程差：
[0058]
δy＝破损路面高程-无破损路面高程＝y
a1-y
a0
ꢀꢀ
(4)
[0059]
此时，δy为负值则代表破损路面高程低于无损路面高程；δy为正值则代表破损路面高程高于无损路面高程。a1高程和a0高程的计算方式，是上述公式(1)中计算y
a0
的部分，即：
[0060]ya0
＝r(1-cost)
ꢀꢀ
(5)
[0061]
而据此计算出在l1这条存在破损的路线上，存在破损的特异点位置距离数据，即bi，以及对应的与无破损的标准路面上的a0运动轨迹之间的高程差。数据汇总如表2所示：
[0062]
表2 a1与a0的高程差数据汇总
[0063]
[0064][0065]
由表2可知，以l1为例，在距离r的起始原点60cm～135cm的这一段路段上，存在着路面破损的情况，有16个路面破损处。