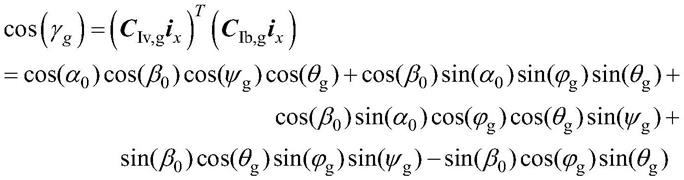
1.本发明涉及航天器控制技术领域，具体涉及一种空间绳系系统的定向部署控制方法。


背景技术：

2.空间绳系系统由空间平台、空间系绳以及末端载荷构成。空间绳系系统作为一种灵活性强、安全性高以及可扩展性好的在轨服务系统，在未来的空间探测、空间侦察、空间维修、空间辅助变轨等任务中均具有良好的应用前景。
3.快速部署是空间绳系系统在轨服务任务中的重要任务之一，实际应用中要实现对目标的近距离观测、监视、维修以及抓捕操作等任务均需要将空间绳系系统部署到距目标一定距离的区域，由于空间绳系系统所配置的传感器限制，如视觉相机，雷达等载荷的正常工作均需空间绳系系统保证对目标的定向，且在任务过程中一直保证对目标的定向，空间绳系系统才能够实时获取其相对目标的相对位姿等信息。空间绳系系统在远距离部署过程中，其相对目标速度信息通常不能够直接通过传感器测量，也就是部分状态信息未知。由于空间绳系系统系统参数部分未知以及干扰等因素的存在，导致其轨道动力学和姿态动力学中均存在不确定性，这些对控制器的最终效果均存在一定的影响。因而考虑空间绳系系统部分状态不可测，以及干扰等因素，设计部分状态未知下的空间绳系系统定向部署控制器十分必要。


技术实现要素：

4.为了克服现有技术的不足，本发明提供一种部分状态未知下的空间绳系系统快速定向部署方法。本发明的目的在于提供一种可以广泛应用于空间绳系系统对目标定向部署控制方法，该控制方法可实现干扰和模型不确定存在情况下，空间绳系系统相对目标位置收敛且姿态稳定，且在整个逼近过程中空间绳系系统一直对目标定向。本发明通过扩张状态观测器实现部分不可直接测量的状态信息如速度信息的获取，并通过扩张状态观测器以及超扭滑模观测器获取系统的干扰和模型不确定的估计。实现了空间绳系系统的快速部署。
5.本发明解决其技术问题所采用的技术方案包括以下步骤：
6.1)建立绳系系统相对目标轨道动力学方程；
7.2)建立绳系系统姿态动力学方程；
8.3)设计空间绳系系统位置扩张观测器；
9.取δ
p
为扩张状态，则扩张观测器设计如下：
[0010][0011][0012]
[0013]
其中，x
p1
，x
p2
，x
p3
分别为ξ
p
，和δ
p
的估计值，为x
p1
的一阶导数，为x
p2
的一阶导数，为x
p3
的一阶导数，f
p
(ξ
p
,x
p2
)为的估计量，ω0为观测器带宽；
[0014]
定义观测器误差为为为且有有有构造新的观测器误差为差为差为差为得到观测器误差动力学方程如下：
[0015][0016]
其中，和分别为和的第j个元素，且j＝1，2，3；a为与状态相关的系数矩阵，β1和β2分别为与速度相关的系数向量和与不确定项相关的系数向量；
[0017]
假设存在正数c1，使得下式成立：
[0018][0019]
则选择观测器带宽为：
[0020]
4)设计位置虚拟控制率α
c
；
[0021]
分别定义位置跟踪误差e1和e2为：e1＝ξ
p
‑
ξ
p,d
，e2＝x
p2
‑
α
c
，其中ξ
p,d
为空间绳系系统期望位置，α
c
为虚拟控制率；虚拟控制率α
c
为：
[0022][0023]
其中，为ξ
p,d
的一阶导数，k1为正定对角矩阵，为的观测偏差，且定义为
[0024]
5)设计位置控制率u
p
；
[0025]
对α
c
求一阶导可得：
[0026][0027]
由于不能直接测量得到，因而将其观测值x
p2
取代得到的估计为：
[0028][0029]
控制器u
p
设计如下：
[0030][0031]
其中，k2为正定矩阵，且满足为正定矩阵；
[0032]
6)姿态指令设计；
[0033]
定义抓捕器视线偏角γ
g
为抓捕机构到目标质心矢量与手爪本体系x轴方向夹角，则：
[0034]
γ
g
＝arccos((c
iv,g
i
x
)
t
(c
ib,g
i
x
))
[0035]
其中，c
iv,g
为惯性坐标系相对空间绳系系统视线坐标系的旋转矩阵。c
ib,g
为惯性坐标系相对空间绳系系统本体坐标系的旋转矩阵，i
x
为x轴向单位矩阵，且有i
x
＝[1 0 0]
t
，则：
[0036][0037]
当θ
g
＝
‑
β0，ψ
g
＝α0时，cos(γ
g
)＝1，此时γ
g
＝0，此时绳系系统轴线指向目标质心，目标最不容易脱离绳系系统的视场范围；
[0038]
因而设计姿态角指令为且有：
[0039][0040]
7)设计空间绳系系统姿态干扰观测器；
[0041]
定义姿态跟踪偏差为：
[0042]
e
a
＝ξ
ad
‑
ξ
a
[0043]
定义滑模面为：
[0044][0045]
其中，为e
a
的一阶导数λ为正定矩阵，为ξ
a
的一阶导数，为ξ
ad
的一阶导数；
[0046]
设计s的观测器为：
[0047][0048]
其中，为s的观测值，为的一阶导数，为ξ
ad
的二阶导数，为s的观测偏差，k＝diag[k
1 k
2 k3]，n＝diag[n
1 n
2 n3]，为观测器待设计参数；
[0049]
设计干扰观测器如下：
[0050][0051]
其中，其中，其中，为γ的一阶导数c＝[c1,c2,c3]为的上界；
[0052]
观测器参数k和n选择如下：
[0053]
[0054]
8)设计姿态控制率u
a
[0055]
则姿态控制率设计如下：
[0056][0057]
其中，k0为正定矩阵，η
d
为的上界，即：即：为γ的观测偏差；
[0058]
通过步骤8空间绳系系统姿态控制器计算出期望控制力矩，空间绳系系统的执行器输出期望控制力矩，实现期望姿态轨迹的跟踪，进而实现空间绳系系统的定向部署。
[0059]
所述空间绳系系统相对目标轨道动力学方程为：
[0060][0061][0062][0063][0064][0065][0066]
其中，ξ
p
＝[l0α0β0]
t
为位置系统状态变量，为ξ
p
的一阶导数，l0为绳系系统到目标视线长度，α0为绳系系统到目标视线面内角，β0为绳系系统到目标视线面外角，为ξ
p
的二阶导数，u
p
为位置控制输入，δ
p
为空间绳系系统相对目标轨道模型不确定以及外界干扰，m
p
为与质量等惯性参数相关项，c
tv
为系绳坐标系相对视线坐标系的旋转矩阵，l0为视线坐标系下目标相对绳系系统的位置，且l0＝[l0,0,0]
t
，为l0的一阶导数，r
vi,g
为视线角变化率到视线角角速度的变换矩阵，为r
vi，g
的一阶导数，
“×”
为叉乘运算符，为非线性速度相关项，n为目标轨道角速度大小，q
l,1
为系绳张力大小，[q
l,2
,q
α
,q
β
]
t
为系绳坐标系下空间绳系系统推力器推力矢量；ω
vi,g
为视线坐标相对惯性坐标系的旋转角速度；n为轨道角速度；
[0067]
所述绳系系统姿态动力学方程为：
[0068][0069]
m
a
＝i
b,g
r
bi,g
[0070][0071][0072][0073]
ξ
a
为姿态系统状态变量，且且为ξ
a
的一阶导数，为ξ
a
的二阶导数，分别为空间绳系系统的滚转角、俯仰角和偏航角，ω
bi,g
为空间绳系系统的旋转角速度。i
b,g
为空间绳系系统的惯量矩阵。r
bi,g
为空间绳系系统姿态角变化率到姿态角速度的变换矩阵。δ
a
为空间绳系系统姿态模型不确定项以及外部干扰项。d
gb
为系绳连接点的位置。c
bt
为空间绳系系统本体坐标系相对系绳坐标系的旋转矩阵。u
a
为姿态控制输入。
c
τ
b,g
为空间绳系系统推力力矩；m
a
为与转动惯量矩阵相关项。
[0074]
所述与状态相关的系数矩阵a为：
[0075][0076]
与速度相关的系数向量β1和与不确定项相关的系数向量β2分别为；
[0077]
b1＝[0 1 0]
t
[0078]
b2＝[0 0 1]
t
。
[0079]
所述选择观测器带宽为：其中
[0080]
本发明的有益效果在于针对空间绳系系统对目标逼近过程中一直保持对目标定向的特殊需求设计了控制方案，通过扩张观测器对空间绳系系统相对目标轨道动力学中不确定性进行估计，并采用反步法设计了控制器。考虑定向问题，设计了姿态控制指令。通过超扭滑模观测器对空间绳系系统姿态动力学中不确定性进行估计并设计了滑模控制器，保证了空间绳系系统对目标定向逼近。采用该技术方案，能够解决绳系系统的部分不可直接测量状态信息的高精度获取难题；对不确定量以及干扰的快速估计难题。能够实现绳系系统在部署过程中快速定向，并且能够保持定向。
附图说明
[0081]
图1是本发明空间绳系系统对目标定向逼近示意图。
[0082]
其中：1
‑
目标；2
‑
末端载荷；3
‑
空间系绳；4
‑
空间平台；
具体实施方式
[0083]
下面结合附图和实施例对本发明进一步说明。
[0084]
步骤1：建立空间绳系系统相对目标轨道动力学方程：
[0085][0086][0087][0088][0089][0090][0091]
其中，ξ
p
＝[l
0 α
0 β0]
t
为位置系统状态变量，为ξ
p
的一阶导数，l0为绳系系统到目标视线长度，α0为绳系系统到目标视线面内角，β0为绳系系统到目标视线面外角，为ξ
p
的二阶导数，u
p
为位置控制输入，δ
p
为空间绳系系统相对目标轨道模型不确定以及外界干扰，m
p
为与质量等惯性参数相关项，c
tv
为系绳坐标系相对视线坐标系的旋转矩阵，l0为视线坐标系下目标相对绳系系统的位置，且l0＝[l0,0,0]
t
，l0为l0的一阶导数，r
vi,g
为视线角变化率到视线角角速度的变换矩阵，为r
vi,g
的一阶导数，
“×”
为叉乘运算符，为非线性速度相关项，n为目标轨道角速度大小，q
l,1
为系绳张力大小，[q
l,2
,q
α
,q
β
]
t
为系绳坐标系下空间绳系系统推力器推力矢量；ω
vi,g
为视线坐标相对惯性坐标系的旋转角速度；n为轨道角速度；
[0092]
步骤2.建立绳系系统姿态动力学方程：
[0093][0094]
m
a
＝i
b,g
r
bi,g
[0095][0096][0097][0098]
ξ
a
为姿态系统状态变量，且且为ξ
a
的一阶导数，为ξ
a
的二阶导数，分别为空间绳系系统的滚转角、俯仰角和偏航角，ω
bi,g
为空间绳系系统的旋
转角速度。i
b,g
为空间绳系系统的惯量矩阵。r
bi,g
为空间绳系系统姿态角变化率到姿态角速度的变换矩阵。δ
a
为空间绳系系统姿态模型不确定项以及外部干扰项。d
gb
为系绳连接点的位置。c
bt
为空间绳系系统本体坐标系相对系绳坐标系的旋转矩阵。u
a
为姿态控制输入。
c
τ
b,g
为空间绳系系统推力力矩。m
a
为与转动惯量矩阵相关项；
[0099]
步骤3.设计空间绳系系统位置扩张观测器；
[0100]
取δ
p
为扩张状态，则扩张观测器设计如下：
[0101][0102][0103][0104]
其中，x
p1
，x
p2
，x
p3
分别为ξ
p
，和δ
p
的估计值，为x
p1
的一阶导数，为x
p2
的一阶导数，为x
p3
的一阶导数，f
p
(ξ
p
,x
p2
)为的估计量，ω0为观测器带宽；
[0105]
定义观测器误差为定义观测器误差为定义观测器误差为且有且有且有进一步构造新的观测器误差为测器误差为测器误差为测器误差为得到观测器误差动力学方程如下：
[0106][0107][0108]
β1＝[0 1 0]
t
[0109]
β2＝[0 0 1]
t
[0110]
其中，和分别为和的第j个元素，且j＝1，2，3；a为与状态相关的系数矩阵，β1和β2分别为与速度相关的系数向量和与不确定项相关的系数向量；
[0111]
假设存在正数c1，使得下式成立：
[0112][0113]
则选择观测器带宽为：其中
[0114]
步骤4.设计位置虚拟控制率α
c
；
[0115]
分别定义位置跟踪误差e1和e2为：e1＝ξ
p
‑
ξ
p,d
，e2＝x
p2
‑
α
c
，其中ξ
p,d
为空间绳系系统期望位置，α
c
为虚拟控制率；虚拟控制率α
c
为：
[0116][0117]
其中，为ξ
p,d
的一阶导数，k1为正定对角矩阵，为的观测偏差，且定义为
[0118]
步骤5.设计位置控制率u
p
；
[0119]
对α
c
求一阶导可得：
[0120][0121]
由于不能直接测量得到，因而将其观测值x
p2
取代得到的估计为：
[0122][0123]
控制器u
p
设计如下：
[0124][0125]
其中，k2为正定矩阵，且满足为正定矩阵；
[0126]
步骤6.姿态指令设计
[0127]
定义抓捕器视线偏角γ
g
为抓捕机构到目标质心矢量与手爪本体系x轴方向夹角，则：
[0128]
γ
g
＝arccos((c
iv,g
i
x
)
t
(c
ib,g
i
x
))
[0129]
其中，c
iv,g
为惯性坐标系相对空间绳系系统视线坐标系的旋转矩阵。c
ib,g
为惯性坐标系相对空间绳系系统本体坐标系的旋转矩阵，i
x
为x轴向单位矩阵，且有i
x
＝[1 0 0]
t
，则：
[0130][0131]
当θ
g
＝
‑
β0，ψ
g
＝α0时，cos(γ
g
)＝1，此时γ
g
＝0，此时绳系系统轴线指向目标质心，目标最不容易脱离绳系系统的视场范围；
[0132]
因而设计姿态角指令为且有：
[0133]
[0134]
步骤7.设计空间绳系系统姿态干扰观测器；
[0135]
定义姿态跟踪偏差为：
[0136]
e
a
＝ξ
ad
‑
ξ
a
[0137]
定义滑模面为：
[0138][0139]
其中，为e
a
的一阶导数λ为正定矩阵，为ξ
a
的一阶导数，为ξ
ad
的一阶导数；
[0140]
设计s的观测器为：
[0141][0142]
其中，为s的观测值，为的一阶导数，为ξ
ad
的二阶导数，为s的观测偏差，k＝diag[k
1 k
2 k3]，n＝diag[n
1 n
2 n3]，为观测器待设计参数；
[0143]
设计干扰观测器如下：
[0144][0145]
其中，其中，其中，为γ的一阶导数c＝[c1,c2,c3]为的上界；
[0146]
观测器参数k和n选择如下：
[0147]
n
i
＞c
i
[0148][0149]
步骤8设计姿态控制率u
a
：
[0150]
则姿态控制率设计如下：
[0151][0152]
其中，k0为正定矩阵，η
d
为的上界，即：即：为γ的观测偏差；
[0153]
通过步骤8空间绳系系统姿态控制器计算出期望控制力矩，空间绳系系统的执行器输出期望控制力矩，实现期望姿态轨迹的跟踪，进而实现空间绳系系统的定向部署。
[0154]
步骤1和步骤2建立出整个空间绳系系统的动力学方程为后续观测器以及控制器的设计的基础；步骤3和步骤7实现系统中不可直接测量状态以及干扰和不确定项的估计，为后续控制器提供信息；步骤4和步骤5设计出空间绳系系统位置控制器，计算出期望控制力。空间绳系系统的执行器输出期望控制力，实现期望位置轨迹的跟踪。步骤6计算出能够实现空间绳系系统定向的期望姿态轨迹，通过步骤8空间绳系系统姿态控制器计算出期望控制力矩。空间绳系系统的执行器输出期望控制力矩，实现期望姿态轨迹的跟踪，进而实现空间绳系系统的定向部署。