1.本技术属于波束成形方法技术领域，尤其涉及一种低信噪比条件下基于自适应压缩感知的波束成形方法。


背景技术：

2.波束成形是基于传声器阵列测量的噪声源识别技术的一种，其本质是一种空间滤波技术，波束成形的思想首先将声源面离散化形成聚焦网格，再运用波束成形方法对声阵列采集到的声场数据进行声源面的聚焦重构，最后通过加强声源所在聚焦点的输出能量的方式来实现声源定位。但在实际应用或者工程实际中，目标声源信号常受到环境噪声信号的干扰，甚至被湮没于其中，导致目标声源信号信息难以被测量和提取，从而影响对目标声源的定位及成像，导致波束成形方法效果不好，影响后续处理工作的进行。


技术实现要素：

3.本技术的目的在于，提出一种与压缩感知相结合的改进波束成形方法，基于自适应和回溯思想，优化现有方案使得压缩感知重构方法运算速度更快且不依赖于稀疏度k值，而后将其与反卷积波束成形法结合，实现更好的定位效果，更强的抗干扰能力。
4.为实现上述目的，本技术采用如下技术方案。
5.一种低信噪比条件下基于自适应压缩感知的波束成形方法，包括如下步骤：
6.步骤a、基于声阵列获取声场声压数据的步骤；
7.具体是指，在测量平面s
h
利用按规则排布的m元传声器阵列，获取含有声源点且呈稀疏分布的声源面s
s
；将声源面s
s
被均分为r个区域，包括n个存在声源的区域；
8.则规则分布的m元传声器阵列接受到的声压信号稀疏表示为：
9.x(t)＝a
·
s(t)+n(t)；
10.式中，在某时刻t，x(t)表示m
×
1维阵列接收信号；a是声源与传声器阵列间的m
×
n维传递矩阵；s(t)表示n
×
1维声源信号；n(t)表示m
×
1维噪声信号；
11.将声源面划分出的每一聚焦点均视作一个潜在声源，则测量面上获得的声压即为单个声源源强与传递矩阵的乘积之和，数学表达式记作：p＝gq；
12.式中：p表示阵列测量面获得的声压，m
×
1维；g表示声源面与阵列测量面之间的传递矩阵，m
×
n维；q表示声源源强，n
×
1维；且
[0013][0014]
式中，g
mn
表示第n个聚焦点与第m个阵元之间的距离，r
n
表示第n个聚焦点与坐标原点之间的距离；
[0015]
步骤b、计算声压互谱矩阵的步骤；
[0016]
声压互谱矩阵c表达式为：c＝pp
h
＝gqq
h
g
h
；当声源为非相干声源，则对qq
h
中的非对角线元素进行简化，qq
h
简化为声压互谱矩阵c表达式为进一步表示为：式中：g
n
为传递矩阵g中的对应列向量；
[0017]
步骤c、计算点传播函数的步骤；
[0018]
基于互谱函数的传统波束成形输出结果b＝ω
h
cω＝ω
h
pp
h
ω；
[0019]
其中，b表示各网格点输出的声功率，ω表示导向向量，ω＝[ω1，ω2…
ω
m
]，得到得到点传播函数声源面声功率
[0020]
步骤d、原信号重构的步骤
[0021]
(1)初始化稀疏度k0＝1，初始化稀疏度估计步长l＝s，s为搜索步长；支撑集f＝φ，φ为空集；
[0022]
(2)计算残差与传感矩阵每列乘积得到相关系数矩阵u＝{u
j
|u
j
＝|<r,φ
j
>|,j＝1,2,...n}，其中φ
j
为传感矩阵的第j列，r为残差，并从相关系数矩阵提出k0个最大值对应的索引值存入索引集f中；
[0023]
(3)基于压缩感知前提条件之一的约束等距性条件，
[0024]
如果则自适应稀释度k＝k0+l，转步骤(2)；
[0025]
式中，y是指声传感器阵列测得的声场数据；δ
k
是介于0到1之间的常数，δ
k
＝0.3；t是指转置矩阵；其中φ是指压缩感知中的传感矩阵；
[0026]
若则到步骤4；
[0027]
(4)利用最小二乘法求解初始余量
[0028]
(5)初始估计信号x＝0，初始化阶段数stage＝1，初始化迭代次数k＝1，初始化索引值集合s＝φ，候选集c＝φ；
[0029]
(6)利用式u＝{u
j
|u
j
＝|<r,φ
j
>|,j＝1,2,...n}计算新的相关系数矩阵，并按照u
j
≥0.5max|u|的标准将对应的索引值存入索引集s中；
[0030]
(7)合并索引值集合t＝f∪s，利用式u＝{u
j
|u
j
＝|<r,φ
j
>|,j＝1,2,...n}计算t中索引值对应原子与余量的相关系数，并提取出k0个最大值对应的索引值存入f
new
中，基于最小二乘法采用式计算估计信号x
new
，并利用r
new
＝y
‑
φ
f
x更新余量；
[0031]
(8)计算两次迭代间的误差并判断是否小于指定误差，若两次迭代间的误差||x
new
‑
x||2≤ε，则停止迭代，否则转步骤(9)，ε是指指定误差，x是指前次误差值；若||r
new
||2≥||r||2，则阶段数加1，stage＝stage+1，l＝stage*s并跳转步骤(6)；若||r
new
||2＜||r||2，则f＝f
new
，r＝r
new
，k＝k+1，转步骤(6)。
[0032]
(9)停止迭代后输出最新得到的估计信号x
new
；方法迭代完毕输出结果后，得到最终想要获得的波束数据。
[0033]
对前述低信噪比条件下基于自适应压缩感知的波束成形方法的进一步改进或优选方法，在测量平面s
h
上将来波视为平面波。
[0034]
其有益效果在于：
[0035]
本技术的低信噪比条件下基于自适应压缩感知的波束成形方法，与常规波束形成法(cbf)、基于正交匹配追踪方法的反卷积波束成形法(omp
‑
damas)相比，在低信噪比条件下对声源定位效果较好，具备较强的抗干扰能力，可作为低信噪比条件下进行声源定位的一种有效补充方法。
附图说明
[0036]
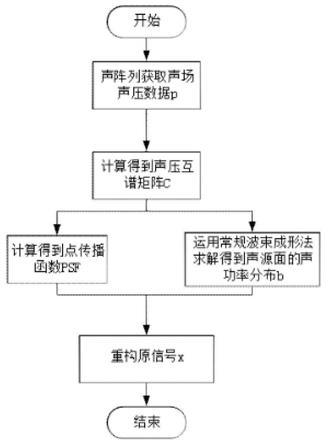
图1是低信噪比条件下基于自适应压缩感知的波束成形方法的流程示意图；
[0037]
图2是传声器阵列信号采集示意图；
[0038]
图3是声源面上声源稀疏表示示意图；
[0039]
图4是无噪声条件下现有技术方法与本技术方法进行重构时间示意图；
[0040]
图5是无噪声条件下现有技术方法与本技术方法的重构误差率示意图；
[0041]
图6是信噪比snr＝30db条件条件下现有技术方法与本技术方法进行重构时间示意图；
[0042]
图7是信噪比snr＝30db条件条件下现有技术方法与本技术方法的重构误差率示意图；
[0043]
图8是信噪比snr＝0db条件现有技术方法与本技术方法进行重构时间示意图；
[0044]
图9是信噪比snr＝0db条件现有技术方法与本技术方法的重构误差率示意图；
具体实施方式
[0045]
以下结合具体实施例对本技术作详细说明。
[0046]
本技术的一种低信噪比条件下基于自适应压缩感知的波束成形方法，包括如下步骤：
[0047]
步骤a、基于声阵列获取声场声压数据的步骤；
[0048]
具体是指，在测量平面s
h
利用按规则排布的m元传声器阵列，获取含有声源点且呈稀疏分布的声源面s
s
；将声源面s
s
被均分为r个区域，包括n个存在声源的区域，空心区域表示该处不存在声源，如图1、图2所示，在具体实施过程中，在测量平面s
h
上将来波视为平面波。
[0049]
则规则分布的m元传声器阵列接受到的声压信号稀疏表示为：
[0050]
x(t)＝a
·
s(t)+n(t)；
[0051]
式中，在某时刻t，x(t)表示m
×
1维阵列接收信号；a是声源与传声器阵列间的m
×
n维传递矩阵；s(t)表示n
×
1维声源信号；n(t)表示m
×
1维噪声信号；
[0052]
反卷积波束成形法以damas和clean方法为主要方式，通过引入点传播(psf)函数逆向求解声源面声压分布，在空间分辨率上较常规波束成形有明显提高。
[0053]
将声源面划分出的每一聚焦点均视作一个潜在声源，则测量面上获得的声压即为
单个声源源强与传递矩阵的乘积之和，数学表达式记作：p＝gq；
[0054]
式中：p表示阵列测量面获得的声压，m
×
1维；g表示声源面与阵列测量面之间的传递矩阵，m
×
n维；q表示声源源强，n
×
1维；且
[0055][0056]
式中，g
mn
表示第n个聚焦点与第m个阵元之间的距离，r
n
表示第n个聚焦点与坐标原点之间的距离；
[0057]
步骤b、计算声压互谱矩阵的步骤；
[0058]
声压互谱矩阵c表达式为：c＝pp
h
＝gqq
h
g
h
；当声源为非相干声源，则对qq
h
中的非对角线元素进行简化，qq
h
简化为声压互谱矩阵c表达式为进一步表示为：式中：g
n
为传递矩阵g中的对应列向量；
[0059]
步骤c、计算点传播函数的步骤；
[0060]
基于互谱函数的传统波束成形输出结果b＝ω
h
cω＝ω
h
pp
h
ω；
[0061]
其中，b表示各网格点输出的声功率，ω表示导向向量，ω＝[ω1，ω2…
ω
m
]，得到得到点传播函数声源面声功率上式给出了互谱成像输出量、点传播函数和声源源强之间的关系，其本质是一个卷积过程。
[0062]
步骤d、原信号重构的步骤
[0063]
正交匹配追踪(omp)、正则化正交匹配追踪(romp)和压缩采样匹配追踪(cosamp)等基础压缩感知重构方法因方法结构简单、复杂度低等特点而受到广泛应用，但不足之处是需要提前预知稀疏度k值，即需要以声源个数为先验信息才可进行运算。而在实际应用中，声源个数一般为未知量，这在一定程度上限制了压缩感知的应用。针对此问题提出的稀疏度自适应匹配追踪(samp)方法，可无需知道稀疏度k值，但该方法又存在运行时间过长的缺点。将cosamp和samp两种方法融合，保留cosamp方法的回溯思想及samp方法的自适应性，得到自适应压缩采样重构方法(简称为samp
‑
cosamp方法)，具体步骤如下：
[0064]
(1)初始化稀疏度k0＝1，初始化稀疏度估计步长l＝s，s为搜索步长；支撑集f＝φ，φ为空集；
[0065]
(2)计算残差与传感矩阵每列乘积得到相关系数矩阵u＝{u
j
|u
j
＝|<r,φ
j
>|,j＝1,2,...n}，其中φ
j
为传感矩阵的第j列，r为残差，并从相关系数矩阵提出k0个最大值对应的索引值存入索引集f中；
[0066]
(3)基于压缩感知前提条件之一的约束等距性条件，如果则自
适应稀释度k＝k0+l，转步骤(2)；式中，y是指声传感器阵列测得的声场数据；δ
k
是介于0到1之间的常数，δ
k
＝0.3；t是指转置矩阵；其中φ是指压缩感知中的传感矩阵；若则到步骤4；
[0067]
(4)利用最小二乘法求解初始余量
[0068]
(5)初始估计信号x＝0，初始化阶段数stage＝1，初始化迭代次数k＝1，初始化索引值集合s＝φ，候选集c＝φ；
[0069]
(6)利用式u＝{u
j
|u
j
＝|<r,φ
j
>|,j＝1,2,...n}计算新的相关系数矩阵，并按照u
j
≥0.5max|u|的标准将对应的索引值存入索引集s中；
[0070]
(7)合并索引值集合t＝f∪s，利用式u＝{u
j
|u
j
＝|<r,φ
j
>|,j＝1,2,...n}计算t中索引值对应原子与余量的相关系数，并提取出k0个最大值对应的索引值存入f
new
中，基于最小二乘法采用式计算估计信号x
new
，并利用r
new
＝y
‑
φ
f
x更新余量；
[0071]
(8)计算两次迭代间的误差并判断是否小于指定误差，若两次迭代间的误差||x
new
‑
x||2≤ε，则停止迭代，否则转步骤(9)，ε是指指定误差，x是指前次误差值；若||r
new
||2≥||r||2，则阶段数加1，stage＝stage+1，l＝stage*s并跳转步骤(6)；若||r
new
||2＜||r||2，则f＝f
new
，r＝r
new
，k＝k+1，转步骤(6)。
[0072]
(9)停止迭代后输出最新得到的估计信号x
new
；方法迭代完毕输出结果后，得到最终想要获得的波束数据。
[0073]
为直观反映方法性能，现设计仿真，在不同信噪比条件下，对各方法的运行时间和误差率进行比较。现有一稀疏信号，信号观测值m＝128，信号长度n＝512。在无噪声及信噪比分别为30db、0db的条件下，分别采用cosamp、samp和本技术方法(简称samp
‑
cosamp方法)进行重构，每组均采用蒙特卡洛方法运行100次。每组从不同稀疏度k值，分别对各方法的运行时间以及重构误差率进行比较，
[0074]
为直观反映本技术方法与现有技术的差异，通过仿真实验，在不同信噪比条件下，首先对运行时间和重构误差进行比较。
[0075]
以某稀疏信号为测试对象，信号观测值m＝128，信号长度n＝512。在无噪声及信噪比分别为30db、0db的条件下，分别采用现有的cosamp、samp和本技术的方法进行重构，每组实验均采用蒙特卡洛方法运行100次。在不同稀疏度k值下，分别对各方法的运行时间以及重构误差率进行比较，
[0076]
仿真所得结果如图4～9所示：
[0077]
综合图7，图8和图9可知，在稀疏度相同时，各算法平均单次运行时间samp算法>samp
‑
cosamp算法>cosamp算法。
[0078]
k＝45为各算法重构误差率的阈值；当k<45时，三种算法重构误差率均较低，小于0.01；当k>45时，各算法的重构误差率均会急速上升，且趋势保持一致。
[0079]
对比图7和图8可知，在无噪声条件下，当k>45时，samp
‑
cosamp算法和samp算法的重构误差随稀疏度变化趋势保持一致，小于cosamp算法，随着噪声的引入，同等稀疏度k值下(k>45)各算法的重构误差明显升高。
[0080]
因此，samp
‑
cosamp保留了cosamp算法的快速性和samp算法的自适应性，其重构精
度介于samp算法和cosamp算法之间，该方法可在实际未知声源个数的声源定位问题中发挥重要作用。
[0081]
最后应当说明的是，以上实施例仅用以说明本技术的技术方案，而非对本技术保护范围的限制，尽管参照较佳实施例对本技术作了详细地说明，本领域的普通技术人员应当理解，可以对本技术的技术方案进行修改或者等同替换，而不脱离本技术技术方案的实质和范围。