1.本发明属于机器人控制技术领域，具体涉及一种面向刚度的机器人加工位姿优化方法。


背景技术：

2.工业机器人具有工作覆盖空间大、可扩展性强、灵活性强、生产效率高的优势，并且成本极具竞争力。国际上一些公司已经实现了机器人磨削系统平台的产业化，成功在一些领域得到有效性验证。然而工业机器人在实际加工过程中仍存在两方面的问题：
3.一、工业机器人的刚度远低于机床的刚度，呈现典型的弱刚性。一般来说，6自由度工业机器人的刚度通常小于1n/μm，而数控机床的刚度通常大于50n/μm。当机器人进行连续路径磨削加工时，总是会有加工过程中产生的磨削力作用在末端执行器上，末端负载会使机器人关节发生变形，并且在末端执行器处产生位置偏差，从而影响工件的加工精度。
4.二、作为空间串联机构，机器人在其运动空间内存在奇异形位。在奇异点处，机器人关节速度易产生突变，进而末端速度与运动控制精度会降低甚至失控，难以准确保证末端位置，因此同样会产生位置偏移，降低加工精度。
5.针对上述问题，现有关于机器人位姿优化的研究，主要在加工中的运动性能和刚度性能这两方面展开。国内外学者已经提出了多种评价指标来定量表征机器人运动性能和刚度性能，并根据这些指标对机器人位姿进行优化。
6.但是目前的研究仍存在一些问题：均聚焦在钻孔和铣削领域，极少涉及磨削加工应用；大多数位姿优化方法并没有做到同时考虑机器人运动性能和刚度两种因素；现有的刚度性能指标由钻孔、铣削等加工任务特点提出，多为单方向(如轴向，切向)指标，没有根据磨削特征提出的刚度指标；而且钻孔只是单点加工，铣削(多为平面)较短的刀路认为刚度恒定，位姿优化算法单一，均没有考虑加工过程的连续性，但磨削是连续加工，保证加工刚度性能最佳的同时要考虑机器人加工姿态的平滑。
7.因此，有必要针对磨削工艺特征，对机器人的加工位姿进行优化，及时调整位姿，避免出现上述问题。


技术实现要素：

8.本发明的目的在于解决现有机器人存在刚性差和奇异形位，从而影响零件加工质量和加工精度的不足之处，而提供一种面向刚度的机器人加工位姿优化方法，即一种以机器人刚度为分析指标和评价对象从而调整机器人加工位姿，以实现零件加工质量提高的方法。
9.为实现上述目的，本发明所提供的技术解决方案是：
10.一种面向刚度的机器人加工位姿优化方法，其特征在于，具体步骤如下：
11.1)进行机器人运动学建模，并获得机器人灵活性能度量指标
12.1.1)采用标准dh建模法进行机器人正逆运动学建模；结合机器人型号建立机器人
dh连杆坐标系和dh模型连杆参数，描述了关节空间与笛卡尔空间的运动映射关系；
13.1.2)基于步骤1.1)建立的模型，采用微分变换法求解描述两空间(即关节空间与笛卡尔空间)运动速度传递关系的雅克比矩阵j(q)，再通过雅克比矩阵条件数的倒数量化任意点到机器人奇异形位的距离，得到灵活性能度量指标di(dexterity index)，公式为：
[0014][0015][0016]
其中，k(j)为雅克比矩阵的条件数，tr(
·
)代表矩阵的迹，m表示矩阵的行数；j(q)前3行元素具有单位mm，后3行均为无量纲元素；
[0017]
对j(q)进行规范化处理后，有
[0018][0019]
则公式为：
[0020][0021][0022]
其中，jn为规范雅克比矩阵，i3×3、o3×3分别为3
×
3的单位矩阵和3
×
3的零矩阵；l为特征长度；
[0023]
2)进行机器人刚度建模，获得机器人末端整体刚度性能指标k
total
及机器人磨削综合刚度评价系数k
grinding
；
[0024]
2.1)基于虚功法(virtual joint method，vjm)建立机器人传统刚度矩阵模型，得到笛卡尔刚度矩阵k公式为：
[0025]
k＝j(q)-tkθj
(q)-1
[0026]
其中，j(q)为机器人雅克比矩阵，k
θ
为关节刚度矩阵；
[0027]
2.2)对步骤2.1)得到的笛卡尔刚度矩阵k取逆，得到笛卡尔柔度矩阵c，即：
[0028][0029]
其中，c
θ
为机器人的关节柔度矩阵，其为k
θ
的逆矩阵，即：
[0030]cθ
＝diag(1/k
θ1
，1/k
θ2
，1/k
θ3
，1/k
θ4
，1/k
θ5
，1/k
θ6
)
[0031]
施加在机器人末端的外力f与其对应的末端位置变化dx间的关系式为：
[0032]
dx＝cf
[0033]
结合实际切削情况，得公式：
[0034]
dx
t
＝c
ftff
[0035]
其中，dx
t
为末端形变的线位移矢量；ff为施加在末端的力矢量；c
ft
为力/平移柔度矩阵；
[0036]
在机器人6轴末端施加各个方向的单位作用力，各方向上所能产生的位移量大小
的集合构成柔度椭球，根据柔度椭球可得末端整体刚度性能指标k
total
公式为：
[0037][0038]
2.3)通过齐次变换矩阵，将步骤2.2)得到的末端柔度椭球转换至接触点得到接触点柔度椭球，完成加工刀具轴的机器人刚度空间转换，公式为：
[0039][0040]
其中，e1、e2、e3为三主轴旋转矢量；
[0041]
2.4)在步骤2.3)转换得到的接触点柔度椭球上，综合考虑曲面法矢方向上的刚度与磨削平面内的最弱刚度，即λn和max(λr，λ
t
)；以λn与max(λr，λ
t
)作为两半轴构成的椭圆的面积用来评价磨削加工的综合刚度性能；从而建立加工时工件曲面法矢方向上的刚度性能与磨削平面内刚度最弱方向上的刚度来综合评价机器人在加工时的刚度性能，用机器人磨削综合刚度评价系数k
grinding
表示：
[0042][0043]
3)优化机器人工作空间
[0044]
3.1)基于步骤1)获得的灵活性能度量指标di对机器人工作空间进行优化，得到机器人灵活工作空间；
[0045]
3.2)在步骤3.1)得到的机器人灵活工作空间基础上，利用步骤2)获得的末端整体刚度性能指标k
total
，对机器人工作空间进一步优化，得到了机器人运动性能和刚度性能较优的工作空间；
[0046]
4)步骤3)优化后的工作空间中，基于步骤2)获得的机器人磨削综合刚度评价系数k
grinding
，以机器人加工轨迹上的所有磨削点机器人加工姿态的整体刚度最优为目标，得到刚度性能目标函数公式为：
[0047][0048]
采用方差最优的规划方法，使得相邻磨削点之间对应关节角的差值尽量均匀，则姿态平滑目标函数可以表示为：
[0049][0050]
其中：
[0051][0052]
表示该轨迹每个关节角度变化的均值；j为机器人六轴的第j个关节，j＝1，
…
，6；θ
ij
为第i个磨削点处机器人第j个关节的关节角度，δθ
ij
表示每个关节在相邻磨削点之间的角度差值；
[0053]
结合实际加工环境，增加约束，构建机器人末端姿态优化数学模型；再采用带精英
策略的快速非支配排序遗传算法处理所述机器人末端姿态优化数学模型，得pareto最优解，根据实际的工艺需要灵活选择实际加工参数；
[0054]
5)利用步骤4)得到的加工参数，优化机器人的加工位姿。
[0055]
进一步地，步骤3)具体为：
[0056]
3.1)在关节空间中离散两关节角，以灵活性能度量指标di为计算指标，绘制机器人关节空间灵活性能等高线图，获得灵活性能指标约束下的机器人灵活工作空间；
[0057]
3.2)以机器人末端整体刚度性能指标k
total
为计算指标，绘制关于θ2和θ3的关节空间刚度性能等高线图，获得考虑末端整体刚度的机器人优刚度工作空间。
[0058]
进一步地，步骤4)中，机器人末端姿态优化数学模型公式为：
[0059][0060]
其中θ
jmin
，θ
jmax
分别为机器人本体转动的上下限，θ
optimization
为优化后关节空间中关节角范围，为各关节额定载荷速度，λ为根据加工需要设定的系数，为对磨削点末端位姿矩阵pi进行机器人运动学求逆，p
initial
为磨削点初始末端位姿，δα为α在[-π，π]上下限内n个均匀离散点的相邻间隔。
[0061]
进一步地，步骤4)中，采用第三代带精英策略的快速非支配排序遗传算法处理所述机器人末端姿态优化数学模型。
[0062]
上述步骤1)和步骤2)的顺序可以调换，或着同时进行。
[0063]
本发明的优点是：
[0064]
1.本发明为表征机器人执行磨削任务时的刚度性能，提出了面向磨削的机器人综合刚度评价系数k
grinding
。针对机器人本体进行研究获取灵活性能与末端刚度性能双重约束下的优化工作空间，以充分发挥机器人本体的运动性能和刚度性能，解决了机器人磨削过程中易产生受力变形的问题，提出了面向刚度的机器人加工位姿优化方法。
[0065]
2.本发明通过将机器人刚度做为分析指标，进行机器人加工位姿优化，从而提高零件加工质量，适用于机器人加工零部件时，自身刚性较差，位姿控制不到位，从而导致零件加工质量和加工精度不满足实际需求的场景。
[0066]
3.在优化工作空间中构建考虑加工位姿与刚度的机器人姿态优化模型，实现连续加工过程中考虑姿态平滑的机器人末端刚度增强。
[0067]
4.本发明优化方法首先探究机器人空间运动性能，引入了基于雅克比矩阵条件数的机器人灵活性能度量指标对机器人的运动性能进行定量分析。接着在机器人刚度模型的基础上构建机器人末端整体刚度性能指标表征其本体末端刚度。进一步考虑加工刀具轴，进行刚度空间转换研究，并结合加工的工艺特点，提出综合刚度评价系数，以表征切削法向以及切削平面内的综合刚度性能。然后同时考虑机器人灵活性和刚度，获取机器人本体运动和刚度性能综合较优的工作空间。随后在优化工作空间中，构建考虑加工位姿与刚度增强的机器人姿态优化模型，以实现连续加工过程中考虑姿态平滑的机器人末端刚度增强。解决了由于机器人刚度较差和奇异形位从而影响零件加工质量和加工精度的问题。使得机器人控制更为合理，在机器人加工领域具有很强的工程应用价值。
附图说明
[0068]
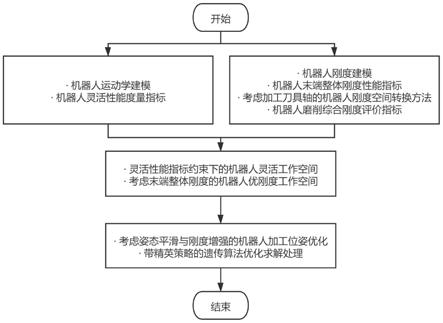
图1是本发明总体流程图；
[0069]
图2是本发明机器人dh连杆坐标系；
[0070]
图3是本发明机器人6轴末端柔度椭球；
[0071]
图4是本发明工件接触点坐标系与接触点柔度椭球；
[0072]
图5是本发明机器人关节空间θ4，θ5灵活性能等高线图；
[0073]
图6是本发明机器人可达工作空间；
[0074]
图7是本发明机器人关节空间θ2，θ3刚度性能等高线图；
[0075]
图8是本发明机器人位姿优化方法验证实验结果图。
具体实施方式
[0076]
以下结合附图和具体实施例对本发明的内容作进一步的详细描述：
[0077]
面向刚度的机器人加工位姿优化方法，包括以下步骤：
[0078]
1)进行机器人运动学建模，并获得机器人灵活性能度量指标
[0079]
1.1)采用标准dh(denavit-hartenberg)建模法进行机器人正逆运动学建模；结合具体机器人型号建立机器人dh连杆坐标系和dh模型连杆参数。机器人dh连杆坐标系如图2所示。
[0080]
1.2)基于步骤1.1)建立的模型，采用微分变换法求解雅克比矩阵j(q)，再通过雅克比矩阵条件数的倒数量化任意点到机器人奇异形位的距离，得到灵活性能度量指标di(dexterity index)，从而定量分析机器人灵活性能，公式为：
[0081][0082][0083]
其中，k(j)为雅克比矩阵的条件数，tr(
·
)代表矩阵的迹，m表示矩阵的行数。di值越大，说明机器人的灵活性能越好。j(q)前3行元素具有单位mm，后3行均为无量纲元素。
[0084]
对j(q)进行规范化处理后，有
[0085][0086]
则公式为：
[0087][0088][0089]
其中，jn为规范雅克比矩阵，i3×3、o3×3分别为3
×
3的单位矩阵和3
×
3的零矩阵；l为特征长度。
[0090]
2)进行机器人刚度建模，获得机器人末端整体刚度性能指标k
total
及机器人磨削综合刚度评价系数k
grinding
；
[0091]
2.1)基于虚功法(virtual joint method，vjm)建立机器人传统刚度矩阵模型，得到笛卡尔刚度矩阵k公式为：
[0092]
k＝j(q)-tkθ
j(q)-1
[0093]
其中，j(q)为机器人雅克比矩阵，k
θ
为关节刚度矩阵；
[0094]
2.2)对步骤2.1)得到的笛卡尔刚度矩阵k取逆，得到笛卡尔柔度矩阵c，即：
[0095][0096]
其中，c
θ
为机器人的关节柔度矩阵，其为k
θ
的逆矩阵，即：
[0097]cθ
＝diag(1/k
θ1
，1/k
θ2
，1/k
θ3
，1/k
θ4
，1/k
θ5
，1/k
θ6
)
[0098]
施加在机器人末端的外力f与其对应的末端位置变化dx间的关系式为：
[0099]
dx＝cf
[0100]
采用柔度矩阵求解c，并结合实际切削情况后，可得公式为：
[0101]
dx
t
＝c
ftff
[0102]
其中，dx
t
为末端形变的线位移矢量；ff为施加在末端的力矢量；c
ft
为力/平移柔度矩阵；
[0103]
根据机器人6轴末端施加各个方向的单位作用力，在该方向上所能产生的位移量大小的集合构建柔度椭球，如图3所示，在3维几何空间中，该集合表示为一个椭球面，称为柔度椭球，3个主轴的方向分别为c
fttcft
特征向量的方向e1、e2、e3，3个半轴长分别为c
fttcft
的特征值开方λ1、λ2、λ3。根据柔度椭球可得末端整体刚度性能指标k
total
公式为：
[0104][0105]
2.3)通过齐次变换矩阵，将步骤2.2)得到的末端柔度椭球转换至接触点得到接触点柔度椭球，如图4所示，完成加工刀具轴的机器人刚度空间转换，公式为：
[0106][0107]
其中e1、e2、e3为三主轴旋转矢量；
[0108]
2.4)在步骤2.3)转换得到的接触点柔度椭球上，综合考虑曲面法矢方向上的刚度与磨削平面内的最弱刚度，即λn和max(λr，λ
t
)。λn与max(λr，λ
t
)作为两半轴构成的椭圆的面
积用来评价磨削加工的综合刚度性能；从而建立加工时工件曲面法矢方向上的刚度性能与磨削平面内刚度最弱方向上的刚度来综合评价机器人在加工时的刚度性能，用机器人磨削综合刚度评价系数k
grinding
表示：
[0109][0110]
3)优化机器人工作空间
[0111]
2.1)在关节空间中离散两关节角，以灵步骤1)获得的灵活性能度量指标di为计算指标，以关节空间θ4，θ5为例，绘制机器人关节空间灵活性能等高线图，如图5所示，获得灵活性能指标约束下的机器人灵活工作空间，如图6所示。
[0112]
3.2)在步骤3.1)得到的机器人灵活工作空间基础上，以步骤2)获得的机器人末端整体刚度性能指标k
total
为计算指标，对机器人工作空间进一步优化，绘制关于θ2与θ3的关节空间刚度性能等高线图，获得考虑末端整体刚度的机器人优刚度工作空间(即得到了机器人运动性能和刚度性能较优的工作空间)，如图7所示。
[0113]
4)步骤3)优化后的工作空间中，基于步骤2)获得的机器人磨削综合刚度评价系数k
grinding
，以机器人加工轨迹上的所有磨削点机器人加工姿态的整体刚度最优为目标，得到刚度性能目标函数公式为：
[0114][0115]
采用方差最优的规划方法，使得相邻磨削点之间对应关节角的差值尽量均匀，则姿态平滑目标函数可以表示为：
[0116][0117]
其中：
[0118][0119]
表示该轨迹每个关节角度变化的均值。j为机器人六轴的第j个关节，j＝1，
…
，6。θ
ij
为第i个磨削点处机器人第j个关节的关节角度，δθ
ij
表示每个关节在相邻磨削点之间的角度差值。
[0120]
结合实际加工环境，增加约束，构建机器人末端姿态优化数学模型，公式为：
[0121][0122]
其中θ
jmin
，θ
jmax
分别为机器人本体转动的上下限，θ
optimization
为优化后关节空间中关节角范围，为各关节额定载荷速度，λ为根据加工需要设定的系数，为对磨削点末端位姿矩阵pi进行机器人运动学求逆，p
initial
为磨削点初始末端位姿，δα为α在[-π，π]上下限内n个均匀离散点的相邻间隔。
[0123]
再采用带精英策略的快速非支配排序遗传算法(nsga-ii)处理上述优化模型，得pareto最优解，根据实际的工艺需要灵活选择实际加工参数；
[0124]
5)利用步骤4)得到的加工参数，优化机器人的加工位姿。
[0125]
本发明优化方法能够有效提高机器人磨削加工时的的加工精度。通过图8所示的验证实验表明，在优化后工作空间中磨削(b)较非工作空间中磨削(a)，去除深度提高了10.11％，具有更好的磨削精度。同时在优化后工作空间的基础上通过机器人姿态优化算法来增强末端刚度(c)，去除深度能再提高8.05％，从而进一步提升磨削精度。
[0126]
以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明公开的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。