1.本发明属于工业机器人抛磨加工技术领域，涉及百叶轮抛磨叶片，具体为一种基于离线编程的百叶轮抛磨叶片路径规划方法。


背景技术：

2.叶片作为航空发动机中重要核心零部件，其加工方法以数控加工、精密锻/铸造、超塑成型为主，并辅以表面抛磨技术来提高叶片表面质量。与砂轮抛磨和砂带抛磨工具相比，百叶轮作为一种砂带的衍生工具，兼具砂轮和砂带抛磨的优点。与手工抛磨和数控抛磨方式相比，机器人具有加工范围大、自由度多、加工成本低的特点，因此，机器人辅助百叶轮抛磨叶片能够满足叶片复杂自由曲面的抛磨加工，可有效提高叶片表面加工质量，缩短叶片制造周期。
3.为实现机器人辅助百叶轮抛磨叶片加工，对抛磨工艺进行规划，高精度的抛磨路径是提高叶片表面加工质量和效率的关键。由于叶片自身的形状结构特点，前缘、后缘半径很小，导致叶片表面曲率变化剧烈，抛磨叶片常采用分区域抛磨的方式，由于在前道工序加工后，叶片表面存在加工余量分布不均匀、存在接刀痕的现象，以及分区域抛磨时需要考虑不同区域之间的抛磨路径拼接问题，从而导致利用叶片理论模型规划的抛磨路径并不能满足实际机器人辅助百叶轮抛磨叶片抛磨路径规划的需求。


技术实现要素：

4.本发明旨在解决叶片表面存在加工余量分布不均匀、存在接刀痕的现象，以及分区域抛磨时需要考虑不同区域之间的抛磨路径拼接的技术问题，提供了一种基于离线编程的百叶轮抛磨叶片路径规划方法。
5.本发明解决其技术问题采用的技术手段是：一种基于离线编程的百叶轮抛磨叶片路径规划方法，包括以下步骤：步骤一、选择与叶片表面各区域相匹配的百叶轮；步骤二、根据步骤一中选定的百叶轮，计算抛磨路径参数；步骤三、根据步骤二中获得的叶片百叶轮抛磨路径参数，生成最优机器人运动轨迹；步骤四、根据步骤三中生成的最优机器人运动轨迹，对机器人运动轨迹进行离线编程仿真，仿真成功后，所规划的抛磨路径作为百叶轮抛磨叶片的抛磨路径进行实际加工。
6.本发明的有益效果包括：第一、通过建立基于形位基准的模型匹配方法，精确重构叶片三维模型，在保留叶片形状信息的同时，可有效实现叶片表面加工余量的均匀分布，避免了由于模型不匹配以及加工余量分布不均匀导致的抛磨路径规划不精确引发的加工精度低的问题；第二、利用表面曲率匹配法，针对叶片表面不同区域选取不同尺寸的百叶轮，实现百叶尺寸选择最大化，在避免抛磨干涉的前提下，提高抛磨效率；
第三、建立基于最大抛磨间距的最小分界线重叠路径规划方法，最大抛磨间距在保证抛磨路径高精度要求的同时，避免了损失加工效率，最小分界线重叠方法针对性的解决了前道工序遗留的接刀痕问题，并克服了在加工叶片表面不同区域时，各区域之间抛磨路径的拼接问题，从而提高了叶片表面加工质量的一致性；第四、本发明在应用于叶片等具有复杂自由曲面表面特征零件的加工时，无需人工示教操作，且可节省离线编程轨迹规划时间，提高编程效率，从而满足智能化、自动化制造过程中的机器人离线编程技术在不同加工制造领域的应用需求。
附图说明
7.为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施方式，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
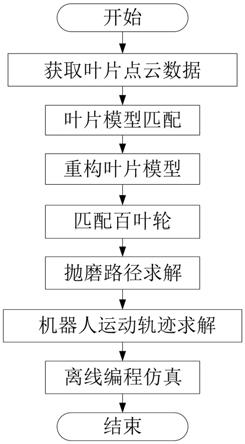
8.图1为本发明所述抛磨路径规划流程图。
9.图2为本发明所述叶片截面线获取示意图。
10.图3为本发明所述基于形位基准的叶片模型匹配示意图图4为本发明所述叶片区域划分示意图（图中（a）为叶片表面网格划分图，图（b）为叶片表面区域划分图）。
11.图5为本发明所述百叶轮尺寸匹配示意图（图中（a）为叶片截面线曲率图，图（b）为叶片百叶轮匹配图）。
12.图6为本发明所述最大抛磨间距确定示意图（图中（a）为百叶轮抛磨叶片方式示意图，图（b）为参数u方向简化抛磨圆示意图，图（c）为最大抛磨间距w示意图）。
13.图7为本发明所述抛磨步长确定示意图。
14.图8为本发明所述边界线调整示意图。
15.图9为本发明所述改进d-h坐标系示意图。
16.图10为本发明所述改进d-h建模示意图。
具体实施方式
17.下面将结合附图对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
18.本发明构建的一种基于离线编程的百叶轮抛磨叶片路径规划方法，如图1所示，包括以下步骤：步骤1，选择与叶片表面各区域相匹配的百叶轮：步骤1.1，利用扫描标定板对三维激光扫描仪进行校准，在待测量叶片表面粘贴定位点，选择三维激光扫描仪中的精细模式对叶片进行扫描，获取叶片表面三维点云数据；步骤1.2，利用三维激光扫描仪自带软件对叶片表面三维点云数据进行精简、去噪、修补预处理，将预处理之后的叶片表面三维点云数据导入到geomagic软件中，利用geomagic软件重构叶片三维模型；
步骤1.3，由geomagic软件重构的叶片三维模型为叶片三角面片三维模型，用一系列平行于叶片截面线方向的平面与叶片三角面片三维模型相交，对所求的交点进行三次标准nurbs曲线拟合，得到一系列相互平行的叶片截面线，如图2所示；步骤1.4，采用基于形位基准的模型匹配方法对重构叶片三维模型和叶片理论模型进行模型匹配，如图3所示，所述的模型匹配包括以下步骤：第一步，重构叶片三维模型和叶片理论模型的模型匹配问题定义为：，式中：、分别是重构叶片三维模型和叶片理论模型，是叶片表面三维点云数据坐标值；叶片表面由一系列截面线积叠而成，积叠轴方向垂直于叶片截面线，则叶片重构三维模型可以表示为：，式中：为位于积叠轴方向高度上的第条截面线；第二步，将模型匹配问题转化为：，式中：、分别是重构叶片三维模型和叶片理论模型上的第条截面线；考虑到叶片截面线属于二维曲线的性质，模型匹配问题可以进一步转换为：，式中：、分别是、的边界；边界由一系列的测量点组成：，式中：为第条截面线上的测量点个数；设定：，，则模型匹配问题可以进一步转换为：，到此，模型匹配问题被简化为条件验证问题；第三步，根据叶片理论模型截面线积叠方式，获得叶片截面线积叠位移矢量图和截面线积叠旋转矢量图；在此基础上，条件验证问题算法如下：假设第(j-1)条截面线满足边界条件，如果第j条截面线同时满足截面线边界条件，则开始验证第(j+1)条截面线的条件；如果第j条截面线不满足边界条件，则在重构叶片三维模型内矫正截面线位置，以满足边界条件；然后，验证第(j-1)条截面线是否仍满足边界条件；如果不满足边界条件，则程序返回到(j-1)继续进行矫正；为减少迭代循环次数，每一条截面线的可移动、可旋转范围已在叶片截面线积叠位移矢量图和截面线积叠旋转矢量图中提前确定；第四步，根据模型匹配后的叶片截面线，重新重构叶片三维模型，从而实现重构叶片三维模型的叶片表面加工余量均匀分布，并生成新的叶片截面线；
步骤1.5，将重构叶片三维模型导入ansys软件中，分析叶片表面曲率分布情况：根据重新生成的截面线个数，选取相同个数的相互平行的平面，沿垂直于截面线方向，与重构叶片三维模型表面相交，这些交线与重新生成的叶片截面线一起，将叶片表面划分为一系列正方形网格，提取网格面片中心点曲率作为网格面片曲率，依据网格面片曲率是否发生突变，将叶片表面划分为前缘、后缘、叶盆和叶背四个区域，如图4所示；步骤1.6，设百叶轮宽度为ab，半径为，抛磨区域的最小曲率半径，百叶轮和叶片表面之间的加工误差为，设加工余量为 ，则加工误差应满足：，为了避免加工误差超出加工余量，则百叶轮的宽度ab应该满足：，并且，为防止百叶轮和抛磨区域发生干涉，必须确保百叶轮半径小于抛磨区域的最小曲率半径，即：，由此依据表面曲率匹配法，分别确定出与叶片前缘、后缘、叶盆和叶背四个区域相匹配且不发生抛磨干涉的百叶轮尺寸，如图5所示；步骤2，根据步骤1中的选定的百叶轮，计算抛磨路径参数；步骤2.1，最大抛磨间距确定，如图6所示：根据叶片表面所划分为一系列正方形网格，提取叶片表面参数点，参数为垂直于截面线方向，即抛磨间距方向，参数为截面线方向，即抛磨步长方向；为精确计算抛磨间距，设当前抛磨路径为，沿参数方向，将百叶轮简化为个间距为1mm的抛磨圆的叠加，依次计算所有抛磨圆圆心正下方点到抛磨路径上点的距离，其最大距离为，当时，说明该抛磨圆参与抛磨，当时，说明该抛磨圆没有参与抛磨，其中为所设定的加工误差；找出所有依次相邻的且满足的抛磨圆，这些抛磨圆确定了百叶轮在该位置时的最大抛磨间距；当百叶轮按照该流程遍历整条抛磨路径时，可计算出当前抛磨路径的最大抛磨间距；步骤2.2，将当前抛磨路径上所有参数点沿参数方向移动最大抛磨间距，得到一组最大抛磨间距数据点，计算该组最大抛磨间距数据点与叶片表面参数点之间的距离，将与该组最大抛磨间距数据点一一对应的距离最小的叶片表面参数点进行三次标准nurbs曲线拟合，得到下一条抛磨路径；步骤2.3，抛磨步长确定，如图7所示：根据叶片各区域分界线参数，确定分界线参数的分布范围，以叶背区域为例，在参数不变的情况下，确定参数的分布范围，根据加工误差计算最大加工带宽度，由于各区域已经选择了曲率相匹配的百叶轮，因此，最大加工带宽度的端点对称于叶片表面抛磨点最小曲率的方向，即两个端点位于同一个圆上；两条分界线根据各自相应的最大加工带宽度同时向叶背区域内部扩展，确定下一百叶轮抛磨点拟合曲线；当两条拟合曲线与其相对应的分界线所覆盖范围实现完全重合相交时，计算两条拟合曲线上距离最近的两抛磨点之间的平均值，设定该抛磨点处的
参数值为，确定该参数位置为最佳抛磨位置；以最佳抛磨位置为基准，以相应的最大加工带宽度重新向两条分界线扩展，得到最终的抛磨步长；同理，依次确定叶片前缘、后缘、叶盆区域的抛磨步长；步骤2.4，以叶片前缘、后缘、叶盆和叶背四个区域之间的原始分界线为基准，根据最小分界线重叠方法调整各区域之间的分界线，如图8所示；设当前抛磨路径为，沿参数方向，计算当前抛磨路径下百叶轮两端抛磨圆圆心正下方点到相应分界线上参数点的距离，若最小距离满足，则将百叶轮继续沿参数方向扩展到下一抛磨路径，并将得到的抛磨路径作为新的区域分界线，若最小距离满足,则当前抛磨路径为最终区域分界线，同理，沿参数方向，计算位于最大抛磨间距两端的抛磨圆圆心正下方点到相应分界线上参数点的距离，若最小距离满足，则将百叶轮继续沿参数方向扩展到下一抛磨步长处，并将所有参数方向上的最终抛磨步长处作为新的区域分界线，若最小距离满足，则当前分界线为最终区域分界线，从而实现叶片不同区域之间抛磨路径的有效拼接，基于此实现了基于最大抛磨间距的最小分界线重叠路径规划；步骤3，根据步骤2中获得的叶片百叶轮抛磨路径参数，生成最优机器人运动轨迹；步骤3.1，机器人运动学正向解析：建立六自由度机器人改进d-h坐标系，如图9所示，六自由度工业机器人有六个旋转关节,首先给每个关节指定坐标系，相邻两个关节之间确立为连杆结构，将连杆坐标系的原点建立在前一个关节坐标系上，即连杆的首端，然后确定从一个关节到下一个关节进行变换的步骤；建立改进d-h坐标系的原则是：(1) 原点为关节轴与轴的交点；(2) 轴沿关节轴的轴向；(3) 轴方向以后一个坐标系轴和当前的轴叉乘确定；(4) 轴方向按照右手定则确定；根据改进的d-h坐标系建立机器人运动学模型，如图10所示，得到机器人的连杆坐标系，d-h参数如下表：根据改进的d-h坐标系，先对杆件长度和杆件扭角进行变换，再对关节平移量和回转量进行变换，从而可求得机器人末端连杆坐标系相对于机器人基座的位姿；用矩阵来描述连杆坐标系之间平移和旋转齐次变换，比如用矩阵表示第一连杆固连坐标系相对于基坐标的位姿；相邻连杆坐标系之间的变换规则为：沿轴平移后绕轴旋转
角度，再沿轴平移后绕轴旋转角度；得到相邻连杆的位姿矩阵：将表中的d-h参数带入到矩阵表达式中得到六组相邻连杆位姿矩阵：h参数带入到矩阵表达式中得到六组相邻连杆位姿矩阵：h参数带入到矩阵表达式中得到六组相邻连杆位姿矩阵：将六个位姿矩阵按照顺序相乘可以得到末端关节相对于基坐标的位姿矩阵，即：式中：
其中：；实现机器人运动学正向解析，即将机器人关节变量作为已知条件对机器人末端变量进行求解；步骤3.2，机器人运动学逆向解析：当机器人末端变量相对于机器人关节变量已知时，即百叶轮抛磨路径已知时，可以求解机器人相应的六个关节的运动角度；采用封闭解中的代数法对机器人进行运动学逆解求解，根据相邻连杆的位姿矩阵表达式，可以直接求出，，求：将等式两边同乘,得到下面的形式：使等式两侧矩阵的一行四列和二行四列的元素对应相等，得到下面等式组：其中p
x
c1+pys1中的各个元素都是已知数，可令k
1=
p
x
c1+pys1,再将等式平方和得到：整理得到：
利用三角代换公式：且整理得到的等式右边的所有元素都是已知的，可使用k2来代替，继续整理得到：此时就可以求出的值：求：将等式两边同左乘,得到下面的形式：使等式左右两侧的矩阵一行三列、二行三列、三行三列的元素对应相等，得到下面的方程等式组：，上面三个式子的左边元素都是已知数，可将三个式子中的第一个和第三个的平方求和得到下面的式子：此时的值就可以求出来了：继续使等式左右两侧的矩阵二行一列、二行二列的元素对应相等，得到下面的等式组:
可得到的值：，上述便得到了的方程表达式，根据计算结果可知的均存在两组解，因此机器人逆运动学共有８组解；步骤3.3，最优机器人运动轨迹求解：求解机器人运动学方程是一个非线性问题，因此六个关节的运动角度有8组解，需要从中找出最优解；机器人逆解的最优解要符合这样的条件：机器人从上一个位置的关节位置运动到下一个关节位置付出的代价应该是最小的；对于不同的关节轴所付出的代价也是不一样的，需要有一个加权因子；又因为关节运动代价与运动速度之间成反比，可以使加权因子设为1/ω；建立运动代价函数：，式中：为机器人上一姿态的关节角、为下一姿态的关节角，为第轴的最大角速度；当机器人关节运动角度满足运动代价函数求得代价最小解时，该组关节运动角度为最优解，作为机器人运动轨迹进行抛磨；步骤4，根据生成的机器人运动轨迹，对机器人运动轨迹进行离线编程仿真，仿真成功后，所规划的抛磨路径作为百叶轮抛磨叶片的抛磨路径进行实际加工，其具体步骤为：步骤4.1，将叶片模型、机器人模型、百叶轮模型以及所搭建的叶片百叶轮抛磨平台，导入到离线编程软件中，根据所规划抛磨路径进行抛磨仿真模拟；步骤4.2，当仿真结果表明按照所规划的抛磨路径进行抛磨时，没有抛磨干涉、无不可达抛磨点现象，可实现叶片所有表面完整抛磨时，证明所规划抛磨路径可实现叶片百叶轮抛磨，可用于实际加工。
19.最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围。