1.本发明涉及燃料电池汽车车速规划和能量管理领域，特别是涉及一种基于分层凸优化的燃料电池汽车节能驾驶方法。


背景技术：

2.通过车对基础设施v2i通信，网联式汽车可以获取道路上的实时信号灯信息，并通过优化车速轨迹实现节能驾驶。燃料电池汽车的节能驾驶是一种包含车速规划和能量管理的耦合问题。该问题的一种解决方案是以最小化动力传动系统的总能耗为目标，进行车速和能量的联合优化，但是超高的计算负担导致联合优化难以实现实时应用。另一种解决方案是将车辆运动规划和动力传动系统控制完全解耦，利用分层优化降低计算量，即首先以最小化车轮处的功率需求为目标进行车速规划，然后基于车速进行能量管理。
3.在现有技术中，涉及燃料电池汽车在信号灯场景中的节能驾驶方法较少，并且难以实现最优性和实时性的平衡。


技术实现要素：

4.本发明的目的在于弥补现有技术的不足，提出一种基于分层凸优化的燃料电池汽车节能驾驶方法，该方法采用分层优化策略，对上层车速规划问题和下层能量管理问题进行凸化，并采用凸优化算法进行快速求解，实现能耗经济性和实时性的平衡。
5.为实现上述目的，本发明采用以下技术方案：一种基于分层凸优化的燃料电池汽车节能驾驶方法，包括以下步骤：
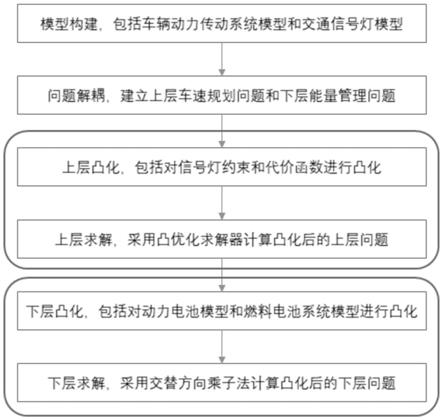
6.s1.建立燃料电池汽车动力传动系统模型和交通信号灯模型；
7.进一步地，步骤s1中所述的燃料电池汽车动力传动系统模型包括车辆纵向动力学模型、电机模型、燃料电池系统模型、动力电池模型和系统功率平衡模型；
8.交通信号灯模型包括信号灯位置和信号相位配时模型。
9.s2.将燃料电池汽车节能驾驶问题解耦为分层优化问题，包括上层车速规划问题和下层能量管理问题；
10.s3.对上层车速规划问题进行凸化，包括对信号灯约束和代价函数进行凸化；
11.s4.利用凸优化求解器对凸化后的车速规划问题进行求解，得到最优车速；
12.s5.对下层能量管理问题进行凸化，包括对动力电池模型和燃料电池系统模型进行凸化；
13.s6.根据上层输出的最优车速，利用交替方向乘子法对凸化后的能量管理问题进行求解，得到最优的控制变量。
14.进一步地，步骤s2中所述的上层车速规划问题和下层能量管理问题，具体如下所示：
15.上层车速规划问题的状态变量为车辆位置和速度，控制变量为车辆加速度，优化目标为总的车轮端需求功率最小，约束条件包括状态变量约束、控制变量约束和信号灯约
束；
16.下层能量管理问题的状态变量为动力电池的荷电状态，控制变量为动力电池的化学功率，优化目标为总的氢耗最小，约束条件包括状态变量约束、控制变量约束、燃料电池系统净功率约束。
17.进一步地，步骤s3中所述的对信号灯约束和代价函数进行凸化，具体如下所示：
18.利用智能驾驶员模型得到车辆位置轨迹上限并确定车辆通过的绿灯窗口，车辆位置轨迹下限需经过所选绿灯窗口的终点并保证不超过位置轨迹上限，车辆的实际到达时间为位置轨迹上下限的终端时间的均值，从而非凸的信号灯约束可以转化为线性时变的车辆位置轨迹约束；
19.利用平均车速近似实时车速，将原本为车速的三次函数的代价函数转化为车速的二次函数。
20.进一步地，步骤s4中所述的凸优化求解器可以为cvx工具包中gurobi、mosek、sdpt3和sedumi的一种。
21.进一步地，步骤s5中所述的对动力电池模型和燃料电池系统模型进行凸化，具体如下所示：
22.将动力电池模型的内阻和开路电压视为常数，从而将动力电池输出功率转化为控制变量的二次函数；将燃料电池系统的氢耗率拟合为电机输入端需求功率的二次函数；从而将目标函数表示为控制变量的凸函数。
23.与现有技术相比，本发明的有益效果是：
24.(1)本发明对包含信号灯约束的上层车速规划问题进行凸化，实现了快速求解；
25.(2)本发明提出的基于分层凸优化的节能驾驶方法，相比于分层动态规划方法，能够在保持相近的能耗经济性的同时实现计算速度的巨大提升。
附图说明
26.图1为本发明所提出的燃料电池汽车节能驾驶优化方法流程图；
27.图2为本发明中信号灯约束凸化示意图。
具体实施方式
28.下面结合附图对本发明的具体实施方式进行详细的描述，但本发明的保护范围不局限于以下所述。
29.如图1所示，一种基于分层凸优化的燃料电池汽车节能驾驶方法，包括以下步骤：
30.s1.建立燃料电池汽车动力传动系统模型和交通信号灯模型
31.燃料电池汽车动力传动系统模型包括车辆纵向动力学模型、电机模型、燃料电池系统模型、动力电池模型和系统功率平衡模型，交通信号灯模型包括信号灯位置和信号相位配时模型。
32.s11.建立车辆纵向动力学模型
33.车辆纵向动力学，如公式(1)所示：
34.[0035][0036]
其中，s，v，m，fr和a分别表示车辆的位置、车速、质量、滚动阻力系数和迎风面积；车辆的加速度f
drv
和f
brk
分别表示车轮处的电机机械力和刹车片制动力；g表示重力加速度；θ表示道路坡度；ρ和cd分别表示空气密度和空气阻力系数。
[0037]
车轮处的需求功率p
dmd
，如公式(2)所示：
[0038]
p
dmd
＝(f
drv
+f
brk
)v
ꢀꢀ
(2)
[0039]
s12.建立电机模型
[0040]
电机转速ω
mot
和转矩t
mot
，如公式(3)和(4)所示：
[0041][0042][0043]
其中，r
whl
是轮胎滚动半径，i
fd
和η
fd
分别是主减速器的传动比和效率。
[0044]
电机的机械功率p
mot,m
和电功率p
mot,e
，如公式(5)和(6)所示：
[0045][0046][0047]
其中，η
mot
表示与ω
mot
和t
mot
有关的电机效率，sgn是符号函数。
[0048]
s13.建立燃料电池系统模型
[0049]
氢气消耗率可以表示为燃料电池系统净功率p
fcs
的函数，如公式(7)所示：
[0050][0051]
燃料电池系统效率η
fcs
，如公式(8)所示：
[0052][0053]
其中，lhv表示氢气的低热值。
[0054]
s14.建立动力电池模型
[0055]
动力电池的等效电路模型，如公式(9)所示：
[0056][0057]
其中，v
bat
，v
oc
，i
bat
，r0，p
bat
和p
oc
分别表示动力电池电压、开路电压、电流、内阻、输出功率和化学功率。v
oc
和r0都是动力电池荷电状态soc的函数。
[0058]
动力电池电流i
bat
，如公式(10)所示：
[0059]
[0060]
电池系统动力学，如公式(11)所示：
[0061][0062]
其中，q
bat
表示电池容量。
[0063]
s15.建立系统功率平衡模型
[0064]
功率平衡模型，如公式(12)所示：
[0065][0066]
其中，η
dc/ac
和η
dc/dc
分别表示dc/ac逆变器和dc/dc变换器的效率。
[0067]
s16.建立交通信号灯模型
[0068]
在总长度为sf的道路上分布着n个交通信号灯路口，第i个信号灯的位置为si∈[0,sf],i∈{1,2,3
…
,n}。对于第i个信号灯，其红灯和绿灯持续时间分别为和其信号周期内时间是行驶时间t的函数，如公式(13)所示：
[0069][0070]
其中是信号灯周期，是的初值。的零点定义在红灯起始时刻。
[0071]
将车辆通过信号灯时的行驶时间记为为了避免闯红灯，车辆需要满足信号灯约束，如公式(14)所示：
[0072][0073]
s2.将燃料电池汽车节能驾驶问题解耦为分层优化问题，包括上层车速规划问题和下层能量管理问题
[0074]
s21.构建上层车速规划问题
[0075]
上层车速规划问题的状态变量为车辆位置和速度，控制变量为车辆加速度，优化目标为总的车轮端需求功率最小，约束条件包括状态变量约束、控制变量约束和信号灯约束，如公式(15)所示：
[0076][0077]
其中，tf为期望的到达时间。
[0078]
s22.构建下层能量管理问题
[0079]
下层能量管理问题的状态变量为动力电池的荷电状态，控制变量为动力电池的化学功率，优化目标为总的氢耗最小，约束条件包括状态变量约束、控制变量约束、燃料电池系统净功率约束上层车速规划问题，如公式(16)所示：
[0080][0081]
s3.对上层车速规划问题进行凸化，包括对信号灯约束和代价函数进行凸化
[0082]
如图2所示，利用智能驾驶员模型得到车辆位置轨迹上限并确定车辆通过的绿灯窗口，车辆位置轨迹下限需经过所选绿灯窗口的终点并保证不超过位置轨迹上限，车辆的实际到达时间为位置轨迹上下限的终端时间的均值，从而非凸的信号灯约束可以转化为线性时变的车辆位置轨迹约束。智能驾驶员模型，如公式(17)所示：
[0083][0084]
其中，a
idm
为智能驾驶员模型的加速度，δv为与前车的速度差，δx为与前车的距离差，s
hd
为智能驾驶员模型的视域范围，p
tss
表示信号灯状态，p
tss
＝0代表绿灯或者看不到信号灯，p
tss
＝1代表红灯，s
*
(v,δv)是期望的与前车距离，如公式(18)所示
[0085][0086]
其中，s0为车头到前车车尾的距离，t
hw
为期望的时距。
[0087]
车辆位置轨迹上限s
upper
，如公式(19)所示：
[0088][0089]
其中，t
f,upper
为位置轨迹上限的到达时间。
[0090]
车辆位置轨迹下限s
lower
，可在距离-时间图中把所选绿灯窗口的终点依次连接得到。
[0091]
最终得到线性时变的车辆位置轨迹约束，如公式(20)所示：
[0092]slower
(t)≤s(t)≤s
upper
(t)
ꢀꢀ
(20)
[0093]
期望的到达时间，如公式(21)所示：
[0094]
[0095]
其中，t
f,lower
为位置轨迹下限的到达时间。
[0096]
利用平均车速近似实时车速，将原本为车速的三次函数的代价函数转化为车速的二次函数，如公式(22)所示：
[0097][0098]
其中，
[0099]
s4.利用凸优化求解器对凸化后的车速规划问题进行求解，得到最优车速
[0100]
凸优化求解器可以为cvx工具包中gurobi、mosek、sdpt3和sedumi的一种。这里采用mosek求解器对凸化后的车速规划问题进行求解，得到最优车速轨迹，作为下层能量管理问题的输入。
[0101]
s5.对下层能量管理问题进行凸化，包括对动力电池模型和燃料电池系统模型进行凸化
[0102]
将动力电池模型的内阻和开路电压视为常数，从而将动力电池输出功率转化为控制变量的二次函数，如公式(23)所示：
[0103][0104]
将燃料电池系统的氢耗率拟合为电机输入端需求功率的二次函数，如公式(24)所示：
[0105][0106]
从而将目标函数表示为控制变量的凸函数，如公式(25)所示：
[0107][0108]
s6.根据上层输出的最优车速，利用交替方向乘子法对凸化后的能量管理问题进行求解，得到最优的控制变量
[0109]
引入对偶变量ζ，将能量管理问题重构并离散化，如公式(26)所示：
[0110][0111]
其中，φ为的n-1列的1向量，ψ为(n-1)
×
(n-1)的下三角1矩阵。
[0112]
按照交替方向乘子法的迭代流程进行求解，得到最优的控制变量和状态变量soc
*
，然后得到最优的燃料电池系统净功率
[0113]
以上所述是本发明的优选实施方式，应被理解为本发明的保护范围并不局限于这样的特定陈述和实施例。本领域的普通技术人员依据本发明的核心思想所进行的改动和变化，都应在本发明所附权利要求的保护范围内。