1.本发明属于机构学领域，特别涉及一种基于对称空间多面体和邻接矩阵的魔方机构构型方法。


背景技术：

2.魔方作为一种玩具，广泛应用于智力开发、娱乐比赛等方面。由于其结构紧凑，组合状态数目众多，适用人群广泛，加之性价比高等优点，已经进入了普通大众的视野。
3.现有魔方中，以经典三阶魔方为代表存在如下的问题，其组合状态数目众多，对于一个普通成年人来讲，想要将其还原，在没有教程的情况下是有一定困难的，更别提低龄儿童了。加之现代社会的电子化，各种电子游戏及短视频的泛滥，长时间的接触对于儿童的正常发育是有害的。魔方具有转轴数量多和一定的对称性等特性，基于此，提出一种基于对称空间多面体和邻接矩阵的魔方机构构型方法对于魔方机构的后续研究及其结构设计是十分必要的。


技术实现要素：

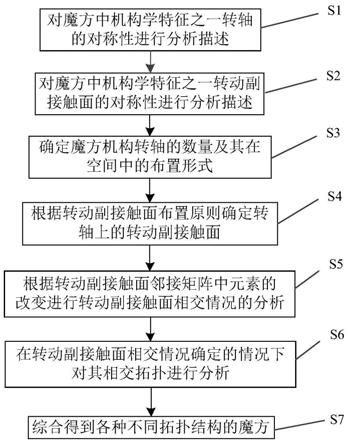
4.本发明针对上述现有技术中的缺陷，基于机构学特征，提出一种基于对称空间多面体和邻接矩阵的魔方机构构型方法。该方法包括对魔方中机构学特征之一转轴的对称性进行分析，并给出其相应的符号表示，对魔方中机构学特征之二转动副接触面的对称性进行分析，确定魔方机构转轴的数量及其在空间中的布置形式，根据转动副接触面布置原则确定转轴上的转动副接触面，根据转动副接触面邻接矩阵中元素的改变进行转动副接触面相交情况的分析，在转动副接触面相交情况确定情况下对其相交拓扑进行分析，综合得到各种不同拓扑结构的魔方。本发明根据魔方中转轴数量多且具有一定对称性等特性，基于对称空间多面体，借助邻接矩阵和相交拓扑分析，综合得到了不同拓扑结构魔方，丰富了魔方的设计研究，提高了魔方的创作兴趣。
5.本发明提供一种基于对称空间多面体和邻接矩阵的魔方机构构型方法，所述方法包括以下步骤：
6.s1、对魔方中机构学特征之一转轴的对称性进行分析，并给出其相应的符号表示；
7.s11、确定魔方中能绕转轴进行重合的所有对称性变换群的表示；
8.s12、结合等价类的定义，确定在对称变换下能重合且交换的转轴间的关系：
[0009][0010]
其中，表示在转动操作下重合的关系；l
jm
表示绕着第j个转轴转动的第m个转轴；
[0011]
s13、确定魔方绕转轴逆时针转动相应角度的操作中被操作的元素完成的相应变换；
[0012]
s14、不能够在魔方的转动规律下通过转动进行重合的转轴被定义为不同的类，所有的转轴通过式(3)进行分类，对魔方转轴的对称性进行一般性的描述；
[0013]
s2、对魔方中机构学特征之二转动副接触面的对称性进行分析：由母线方程对转
动副接触面进行参数化表示，且转轴上的转动副接触面必须相同，表示如下：
[0014][0015]
其中，p表示转轴上的第p个转动副接触面；mj表示绕着第j个转轴转动的转轴个数；表示mj的约数并满足即将mj个转轴分成组，每组有个转轴且被称为分转轴；
[0016]
s3、确定魔方机构转轴的数量及其在空间中的布置形式：利用具有对称特性的空间多面体布置魔方转轴，以多面体的中心为原点，所有转轴从原点向外射出，第二端通过多面体的顶点、棱的等分点、面的中心以及能够使得转轴满足对称性布置的点布置；
[0017]
s4、根据转动副接触面布置原则确定转轴上的转动副接触面：根据所需综合魔方的拓扑类型，结合转轴确定的情况下转动副接触面的布置原则，对同一类不同转轴上的转动副接触面进行对称性的布置；
[0018]
s5、根据转动副接触面邻接矩阵中元素的改变进行转动副接触面相交情况的分析；
[0019]
s51、将魔方抽象成一个由单连通面σ0包络形成的空间体σ，假定该空间体σ上有转动副接触面，将未进行转动前且能够保持单连通面σ0完整性的状态称为初始状态；
[0020]
s52、空间旋转曲面0πi会和σ0相交，轮廓记作0si，则转动副接触面πi是指初始状态下空间旋转曲面0πi与单连通面σ0相交的轮廓0si包围形成的属于0π
1i
的部分，即有：
[0021][0022]
s53、面σ0上由轮廓0si沿着转轴方向的部分记作0σ
πi
；属于面σ0，并且转动副接触面πi、π
i+1
与面σ0的相交轮廓0si、0s
i+1
之间的部分记作0σ
πi(i+1)
上；
[0023]
s54、借鉴花朵上花瓣的内外相对位置关系，对同一转轴上的不同转动副接触面的相对位置关系进行描述；
[0024]
s55、魔方的可动构件是通过转动副接触面和空间体σ的面σ0的相交后得到，则转动副接触面的相交均设为指转动副接触面在空间体σ的面σ0上的相交；
[0025]
s56、借鉴图论中邻接矩阵的概念建立转动副接触面的邻接矩阵，对魔方中转动副接触面的布置规律进行研究，选取魔方中的转动副接触面为研究对象并且按照一定的规则标号，其邻接矩阵为：
[0026]
am(g)＝[(am)
ij
]n×nꢀꢀꢀ
(6)
[0027]
其中，(am)
ij
表示转动副接触面是否相交，即：
[0028][0029]
s6、在转动副接触面相交情况确定的情况下对其相交拓扑进行分析：当魔方的转轴个数、转轴布置方式、转轴上转动副接触面和转动副接触面相交情况均相同时，分析转动
副接触面相交拓扑对魔方机构拓扑结构的影响，相交的转动副接触面在魔方的外表面有相交公共区域，根据这个区域是否为一个点对魔方的拓扑结构进行分析；
[0030]
s7、综合得到各种不同拓扑结构的魔方。
[0031]
进一步，所述步骤s56中邻接矩阵能对转动副接触面的拓扑关系进行全面的描述，其包括如下特点：
[0032]
s561、邻接矩阵为实对称矩阵，其中的元素只含有1和0两种，若对角线元素为0，则表示转动副接触面之间是不存在相交关系的；
[0033]
s562、邻接矩阵中转动副接触面的重合是随着转轴的重合而进行的，转轴的重合是以分转轴为单元进行的，分转轴所绕着转动的转轴上的转动副接触面要同时和分转轴上的转动副接触面相交或不相交，其对应的邻接矩阵中的元素是1或0；
[0034]
s563、无论转轴上有几个转动副接触面，共线反向的转轴上的转动副接触面对应的邻接矩阵中的元素为0；同一个转轴上的不同的转动副接触面对应的邻接矩阵中的元素为0；
[0035]
s564、当转动副接触面a和转动副接触面b相交时，转动副接触面a一定和转动副接触面b外侧的转动副接触面都相交：按照转动副同一个转轴上转动副接触面由外到内的相对位置，设转轴lu上有u
t
个转动副接触面转轴lv上有v
t
个转动副接触面根据转动副接触面编号规则，则有：
[0036][0037]
当转动副接触面和相交时，则转动副接触面必定和转动副接触面相交；同理，转动副接触面必定和转动副接触面相交。与此同时，转动副接触面必定和转动副接触面分别相交；
[0038]
s565、当任意一个转动副接触面所在的行或者列对应的元素均为0时，这个转动副接触面不会与任意的转动副接触面相交形成可交换构件，则这样的转动副接触面不存在。
[0039]
进一步，所述步骤s11具体包括以下步骤：
[0040]
s111、假定魔方中含有n个转轴，记为l1、l2、
…
、ln，选定绕第j个转轴lj(j《n)转动；
[0041]
s112、根据魔方的转动规律，有mj(mj《n)个转轴绕该转轴lj转动，记为
[0042]
s113、所述mj个转轴在转动的整数倍后仍保持重合，记为
[0043]
s114、所述mj个转轴上转动副接触面的布置需根据转动角度进行确定，按逆时针的顺序选取个连续的转轴为一组，即表示为个连续的转轴为一组，即表示为
[0044]
s115、将绕着转轴lj转动重合的mj个转轴表示为对称性变换群
[0045][0046]
s116、魔方中能够绕着转轴进行重合的所有的对称性变换群g为：
[0047][0048]
优选的，所述步骤s54具体包括以下步骤：
[0049]
s541、类似于对花朵的观察，从正视于转轴的方向对转动副接触面在外表面σ0的相对位置进行观察，相对于观察位置距离越近，转动副接触面直径越小，转动副接触面越是靠近内侧，反之越靠近外侧；
[0050]
s542、根据同一个转轴上的转动副接触面相对位置关系对转动副接触面进行标号。转轴li上有j个转动副接触面，由外侧到内侧标号依次增大，分别记作π
i1
、π
i2
、
……
、π
ij
。
[0051]
进一步，所述步骤s11中当魔方的转轴绕着其中一个转轴lj(j《n)进行转动重合之后，还可继续绕着这些被转动的转轴l
j1
、l
j2
、
……
、l
jm
中的一个继续进行转动重合，按照魔方的转动规律，使得魔方中的转轴能够重合的对称变换构成的集合即为魔方中转轴的对称性变换群。
[0052]
优选的，所述步骤s3中所述转轴的布置原则为所有转轴至少构成同一类，且同一类转轴中至少有两个转轴；所述步骤s4中转轴确定的情况下的转动副接触面的布置原则为要确保同一类转轴上转动不同角度之后重合的转轴有相同的转动副接触面，且要根据所有转动副接触面对于整个魔方的切割进行是否相交。
[0053]
优选的，所述步骤s3中转轴第二端可布置在多面体的顶点、棱的等分点、面的中心以及能够使得转轴满足对称性布置的点四者中的任意一种或多种组合。
[0054]
与现有技术相比，本发明的技术效果为：
[0055]
1、本发明设计的一种基于对称空间多面体和邻接矩阵的魔方机构构型方法，根据魔方中转轴数量多且具有一定的对称性等特性，基于对称的空间多面体给出了魔方转轴的设计，并给出了魔方转动副接触面的布置原则，对魔方的设计奠定了基础和保障。
[0056]
2、本发明设计的一种基于对称空间多面体和邻接矩阵的魔方机构构型方法，借助邻接矩阵对魔方中转动副接触面的相交情况进行相应的描述和分析，根据转动副接触面之间邻接矩阵对应元素的值确定转动副接触面之间的相交关系，进而初步确定魔方的拓扑结构；通过对魔方机构转动副接触面的相交拓扑进行分析和判断，以进一步确定魔方机构的拓扑结构。
[0057]
3、本发明设计的一种基于对称空间多面体和邻接矩阵的魔方机构构型方法，所提方法对魔方的后续研究和设计均具有理论指导意义，不仅更好地适应了不同构态的需求，也丰富了魔方的设计研究，提高了魔方的创作兴趣。
附图说明
[0058]
通过阅读参照以下附图所作的对非限制性实施例所作的详细描述，本技术的其它特征、目的和优点将会变得更明显。
[0059]
图1为本发明的基于对称空间多面体和邻接矩阵的魔方机构构型方法的流程图；
[0060]
图2a为本发明的正六面体中转轴过6个面中心的布置示意图；
[0061]
图2b为本发明的正六面体中转轴过8个顶点的布置示意图；
[0062]
图2c为本发明的正六面体中转轴过棱的中点的布置示意图；
[0063]
图2d为本发明的正六面体中转轴过棱的四等分点的布置示意图；
[0064]
图2e为本发明的正六面体中转轴过6个面的中心和8个顶点的布置示意图；
[0065]
图2f为本发明的正六面体中转轴过6个面的中心和棱的中点的布置示意图；
[0066]
图2g为本发明的正六面体中转轴过8个顶点和棱的中点的布置示意图；
[0067]
图2h为本发明的正六面体中转轴过8个顶点和棱的四等分点的布置示意图；
[0068]
图2i为本发明的正六面体中转轴过6个面的中心和棱的四等分点的布置示意图；
[0069]
图3a为本发明的转轴过六面体的顶点一的示意图；
[0070]
图3b为本发明的转轴过六面体的顶点二的示意图；
[0071]
图3c为本发明的转轴过六面体的顶点三的示意图；
[0072]
图3d为本发明的转轴过六面体棱的中点一的示意图；
[0073]
图3e为本发明的转轴过六面体棱的中点二的示意图；
[0074]
图3f为本发明的转轴过六面体棱的中点三的示意图；
[0075]
图4为本发明的初始状态下空间旋转曲面、转动副接触面、空间多面体间关系示意图；
[0076]
图5为本发明的花朵上花瓣的内外相对位置关系示意图；
[0077]
图6a为本发明的转轴过正六面体面心且每个转轴上有2个转动副接触面的类型一示意图；
[0078]
图6b为本发明的转轴过正六面体面心且每个转轴上有2个转动副接触面的类型二示意图；
[0079]
图6c为本发明的转轴过正六面体面心且每个转轴上有2个转动副接触面的类型三示意图；
[0080]
图6d为本发明的转轴过正六面体面心且每个转轴上有2个转动副接触面的类型四示意图；
[0081]
图6e为本发明的转轴过正六面体面心且每个转轴上有2个转动副接触面的类型五示意图；
[0082]
图6f为本发明的转轴过正六面体面心且每个转轴上有2个转动副接触面的类型六示意图；
[0083]
图7a为本发明的转轴过正六面体过面心的类型一的示意图；
[0084]
图7b为本发明的转轴过正六面体过面心的类型二的示意图；
[0085]
图7c为本发明的转轴过正六面体过面心的类型三的示意图；
[0086]
图7d为本发明的转轴过正六面体过面心的类型四的示意图；
[0087]
图7e为本发明的转轴过正六面体过面心的类型五的示意图；
[0088]
图7f为本发明的转轴过正六面体过面心的类型六的示意图；
[0089]
图8a为本发明的转轴过正六面体顶点时转动副接触面分布情况类型一及其对应魔方；
[0090]
图8b为本发明的转轴过正六面体顶点时转动副接触面分布情况类型二及其对应
魔方；
[0091]
图8c为本发明的转轴过正六面体顶点时转动副接触面分布情况类型三及其对应魔方；
[0092]
图8d为本发明的转轴过正六面体顶点时转动副接触面分布情况类型四及其对应魔方；
[0093]
图8e为本发明的转轴过正六面体顶点时转动副接触面分布情况类型五及其对应魔方；
[0094]
图8f为本发明的转轴过正六面体顶点时转动副接触面分布情况类型六及其对应魔方；
[0095]
图9a为本发明的转轴过正六面体棱中点时转动副接触面分布情况类型一及其对应魔方；图9b为本发明的转轴过正六面体棱中点时转动副接触面分布情况类型二及其对应魔方；图9c为本发明的转轴过正六面体棱中点时转动副接触面分布情况类型三及其对应魔方；
[0096]
图9d为本发明的转轴过正六面体棱中点时转动副接触面分布情况类型四及其对应魔方；
[0097]
图10a为本发明的转动副接触面相交拓扑对魔方机构拓扑结构的影响的类型一的示意图；
[0098]
图10b为本发明的转动副接触面相交拓扑对魔方机构拓扑结构的影响的类型二的示意图；
[0099]
图11a为本发明的正六面体转轴过棱中心十二轴魔方的类型一示意图；
[0100]
图11b为本发明的正六面体转轴过棱中心十二轴魔方的类型二示意图。
具体实施方式
[0101]
下面结合附图和实施例对本技术作进一步的详细说明。可以理解的是，此处所描述的具体实施例仅仅用于解释相关发明，而非对该发明的限定。另外还需要说明的是，为了便于描述，附图中仅示出了与有关发明相关的部分。
[0102]
需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的特征可以相互组合。下面将参考附图并结合实施例来详细说明本技术。
[0103]
图1示出了本发明的基于对称空间多面体和邻接矩阵的魔方机构构型方法，该方法包括以下步骤：
[0104]
s1、对魔方中机构学特征之一转轴的对称性进行分析，并给出其相应的符号表示。
[0105]
s11、确定魔方中能绕转轴进行重合的所有对称性变换群的表示。
[0106]
s111、假定魔方中含有n个转轴，记为l1、l2、
…
、ln，选定绕第j个转轴lj(j《n)转动。
[0107]
s112、根据魔方的转动规律，有mj(mj《n)个转轴绕该转轴lj转动，记为l
j1
、l
j2
、
…
、l
jmj
。
[0108]
s113、mj个转轴在转动的整数倍后仍保持重合，记为其中表示mj的约数并满足即将mj个转轴分成组，每组有个转轴且被称为分转轴。
[0109]
s114、mj个转轴上转动副接触面的布置需根据转动角度进行确定，按逆时
针的顺序选取个连续的转轴为一组，即表示为个连续的转轴为一组，即表示为
[0110]
s115、将绕着转轴lj转动重合的mj个转轴表示为对称性变换群
[0111][0112]
s116、魔方中能够绕着转轴进行重合的所有的对称性变换群g：
[0113][0114]
当魔方的转轴绕着其中一个转轴lj(j《n)进行转动重合之后，还可继续绕着这些被转动的转轴l
j1
、l
j2
、
……
、l
jm
中的一个继续进行转动重合，按照魔方的转动规律，使得魔方中的转轴能够重合的对称变换构成的集合即为魔方中转轴的对称性变换群。
[0115]
s12、结合等价类的定义，确定在对称变换下能重合且交换的转轴间的关系：
[0116][0117]
其中，表示在转动操作下重合的关系；l
jm
表示绕着第j个转轴转动的第m个转轴；。
[0118]
s13、确定魔方绕转轴逆时针转动相应角度的操作中被操作的元素完成的相应变换。
[0119]
s14、不能够在魔方的转动规律下通过转动进行重合的转轴被定义为不同的类，所有的转轴通过式(3)进行分类，对魔方转轴的对称性进行一般性的描述。
[0120]
s2、对魔方中机构学特征之二转动副接触面的对称性进行分析：由母线方程对转动副接触面进行参数化表示，且转轴上的转动副接触面必须相同，表示如下：
[0121][0122]
其中，p表示转轴上的第p个转动副接触面。
[0123]
s3、确定魔方机构转轴的数量及其在空间中的布置形式：利用具有对称特性的空间多面体布置魔方转轴，以多面体的中心为原点，所有转轴从原点向外射出，第二端通过多面体的顶点、棱的等分点、面的中心以及能够使得转轴满足对称性布置的点四者中的任意一种或多种组合布置；转轴的布置原则为所有转轴至少构成同一类，且同一类转轴中至少有两个转轴。
[0124]
在一个具体实施例中，以正六面体为例，以其中心为原点，所有的转轴交于原点，另一个点可通过正六面体的顶点、棱的等分点、面的中心等，可以得到如图2a～2i所示的九种可能。除此之外，还可以选取棱的n等分点、过顶点、过面的中心点的组合，只要保证所组
合的魔方转轴满足转轴的布置原则即可，如转轴过正六面体的顶点，转轴过正六面体棱的中点，可以得到如图3a～3f所示的六种可能。除了借助正六面体进行转轴的布置之外，还可以借助任意具有对称特性的多面体进行类似转轴的布置。
[0125]
s4、根据转动副接触面布置原则确定转轴上的转动副接触面：根据所需综合魔方的拓扑类型，结合转轴确定的情况下转动副接触面的布置原则，对同一类不同转轴上的转动副接触面进行对称性的布置；其中转轴确定的情况下的转动副接触面的布置原则为要确保同一类转轴上转动不同角度之后重合的转轴有相同的转动副接触面，且要根据所有转动副接触面对于整个魔方的“切割”进行是否相交。
[0126]
s5、根据转动副接触面邻接矩阵中元素的改变进行转动副接触面相交情况的分析。
[0127]
s51、将魔方抽象成一个由单连通面σ0包络形成的空间体σ，假定该空间体σ上有转动副接触面，将未进行转动前且能够保持单连通面σ0完整性的状态称为初始状态。
[0128]
s52、空间旋转曲面0πi会和σ0相交，轮廓记作0si，则转动副接触面πi是指初始状态下空间旋转曲面0πi与单连通面σ0相交的轮廓0si包围形成的属于0π
1i
的部分，即有：
[0129][0130]
s53、面σ0上由轮廓0si沿着转轴方向的部分记作0σ
πi
；属于面σ0，并且转动副接触面πi、π
i+1
与面σ0的相交轮廓0si、0s
i+1
之间的部分记作0σ
πi(i+1)
上。
[0131]
在一个具体实施例中，以正六面体为例，当i＝1时，初始状态下的空间旋转曲面、转动副接触面、空间多面体之间的关系示意图如图4所示。
[0132]
s54、同一多花上会有不同的花瓣，不同花瓣会有相对位置关系，如图5所示，花朵上有多个花瓣，由外侧到内侧给花瓣进行标号π
f1
、π
f2
、π
f3
、π
f4
。同样地，魔方同一转轴上的多个转动副接触面类似于同一朵花上的不同花瓣，借鉴花朵上花瓣的“内外”相对位置关系对同一转轴上的不同转动副接触面的相对位置关系进行描述。
[0133]
s541、类似于对花朵的观察，从正视于转轴的方向对转动副接触面在外表面σ0的相对位置进行观察，相对于观察位置距离越近，转动副接触面直径越小，转动副接触面越是靠近内侧，反之越靠近外侧。
[0134]
s542、根据同一个转轴上的转动副接触面相对“位置”关系对转动副接触面进行标号。转轴li上有j个转动副接触面，由外侧到内侧标号依次增大，分别记作π
i1
、π
i2
、
……
、π
ij
。如图5所示，一个转轴上有2个转动副接触面π1、π2。根据以上描述，这2个转动副接触面相对转轴而言，π2在最内侧，π1在最外侧。
[0135]
s55、魔方的可动构件是通过转动副接触面和空间体σ的面σ0的相交后得到，则转动副接触面的相交均设为指转动副接触面在空间体σ的面σ0上的相交。
[0136]
s56、借鉴图论中邻接矩阵的概念建立转动副接触面的邻接矩阵，对魔方中转动副接触面的布置规律进行研究，选取魔方中的转动副接触面为研究对象并且按照一定的规则标号，其邻接矩阵为：
[0137]
am(g)＝[(am)
ij
]n×nꢀꢀꢀ
(6)
[0138]
其中，(am)
ij
表示转动副接触面是否相交，即：
[0139][0140]
其中，邻接矩阵能对转动副接触面的拓扑关系进行全面的描述，其包括如下特点：
[0141]
s561、邻接矩阵为实对称矩阵，其中的元素只含有1和0两种，若对角线元素为0，则表示转动副接触面之间是不存在相交关系的。
[0142]
s562、邻接矩阵中转动副接触面的重合是随着转轴的重合而进行的，转轴的重合是以分转轴为单元进行的，分转轴所绕着转动的转轴上的转动副接触面要同时和分转轴上的转动副接触面相交或不相交，其对应的邻接矩阵中的元素是1或0。
[0143]
s563、无论转轴上有几个转动副接触面，共线反向的转轴上的转动副接触面对应的邻接矩阵中的元素为0；同一个转轴上的不同的转动副接触面对应的邻接矩阵中的元素为0。
[0144]
s564、当转动副接触面a和转动副接触面b相交时，转动副接触面a一定和转动副接触面b外侧的转动副接触面都相交：按照转动副同一个转轴上转动副接触面由外到内的相对位置，设转轴lu上有u
t
个转动副接触面转轴lv上有v
t
个转动副接触面根据转动副接触面编号规则，则有：
[0145][0146]
当转动副接触面和相交时，则转动副接触面必定和转动副接触面相交；同理，转动副接触面必定和转动副接触面相交。与此同时，转动副接触面必定和转动副接触面分别相交。
[0147]
s565、当任意一个转动副接触面所在的行或者列对应的元素均为0时，这个转动副接触面不会与任意的转动副接触面相交形成可交换构件，则这样的转动副接触面不存在。
[0148]
在一个具体实施例中，以转轴过正六面体面心，并且每个转轴上有两个转动副接触面为例，给出其邻接矩阵的一般表示：
[0149][0150]
由于邻接矩阵是实对称阵，只给出右上三角的表达式。根据邻接矩阵中元素的特点给出了元素的参数表示ai(i＝1,2,
……
,12)，结合邻接矩阵的特点，这些参数满足如下关系：
[0151]
若a2＝1，则a1＝1；若a4＝1，则a3＝1；若a6＝1，则a5＝1；若a8＝1，则a7＝1；
[0152]
若a
10
＝1，则a9＝1；若a
12
＝1，则a
11
＝1；若a5＝1，则a1＝1；若a6＝1，则a2＝1；
[0153]
若a7＝1，则a3＝1；若a8＝1，则a4＝1；若a
11
＝1，则a9＝1；若a
12
＝1，则a
10
＝1；
[0154]
除了满足上述关系，式(9)中的元素ai(i＝1,2,
……
,12)还需要根据邻接矩阵中元素的特点进行0或者1的任意组合，得到所有的转动副接触面之间的相交情况，图6a～6f给出了部分参数值及其对应的魔方机构模型。
[0155]
在另一个具体实施例中，以转轴过正六面体面心，并且每个转轴上只有一个转动副接触面为例，给出其邻接矩阵的一般表示：
[0156][0157]
当对式(10)中邻接矩阵的参数按照魔方机构中转动副接触面的相交原则进行组合时，就会得到所有的转动副接触面相交的情况。这里给出部分参数值及其对应的转动副接触面相交情况下的魔方机构模型，如图7a～7d为b1＝b2＝b3＝1的可能结果，如图7e为b1＝1且b2＝b3＝0的可能结果，如图7f为b1＝b2＝b3＝0的可能结果，6个转轴在空间都是均匀分布。图7a是一般的经典三阶魔方，每个转轴上的只有一个平面型的转动副接触面，并可绕任意一个转轴转动90
°
的整数倍后还可继续绕连续转轴转动；图7b的每个转轴上都有一个完全相同的曲面型的转动副接触面，虽然它的外形和图7a不一样，但它们的转动副接触面
都满足式(4)，具有相同的拓扑结构、状态数以及转动特性，因此它们两个本质上是相同的；图7c所示的魔方中，含有3种不同的转动副接触面，共线的两个转轴上有相同的转动副接触面，不共线的转轴上的转动副接触面是不相同的，其实这是三阶魔方能够转动的一般情形，此时魔方只能构绕着算定的转轴转动180
°
的整数倍才能够实现连续转动操作，完成可重构运动；图7d所示的魔方中，其本质和图7c所示的魔方是一样的，但是由于转动副接触面的参数不同，就会给人一种视觉上的“不同”；图7e所示的魔方中，假定它含有6个转轴，每个转轴上都有一个转动副接触面，共线的两个转轴上都有相同的转动副接触面，但是由于转轴4l
h3
、4l
h6
对应的转动副接触面没有其余的转动副接触面相交，因此这两个转轴以及相应的转动副接触面是可以去掉的；更特殊地，图7f所示的魔方中，假定它含有6个转轴，每个转轴上都有一个转动副接触面，共线的两个转轴上都有相同的转动副接触面，但是由于任意的两个转动副接触面之间都没有相交，从本质上说这不是一个魔方。
[0158]
通过图7a～7f的例子也就可以直观明了的解释了为什么有的魔方可以转动90
°
的整数倍后就可以继续转动(图7a所示)，而有的魔方只有在转动180
°
的整数倍后才可以继续转动(图7c所示)。另一方面，通过上述综合出的这几个魔方，深刻地解释了转动副接触面相交情况及其邻接矩阵对魔方拓扑结构的优势。
[0159]
同理，在第三个具体实施例中，当转轴通过正六面体的8个顶点时，通过在转轴上布置满足式(4)的转动副接触面，给出转动副接触面相交情况的邻接矩阵，就可以得到相应的魔方机构。这里仅给出部分模型，如图8a～8f所示，邻接矩阵不予赘述。
[0160]
图8a和图8b所示的魔方，每个图的左边是魔方机构图，右边是魔方拓扑结构图，一种是为了表示新构型的结果，一种是显示内部应用的方法，是用两种不同形式表达出来。8个转轴上的转动副接触面均相同，本质上来讲这两种魔方具有相同的拓扑结构、状态数以及转动特性，因此它们两个是相同的。魔方转轴也可以只通过8个顶点中的一部分，只要转轴的布置满足对称性要求即可。例如图8c、图8d、图8e所示的两种布置方式，此时在转轴上布置相应的转动副接触面就可以得到对应拓扑结构的魔方。图8f所示的魔方，含有两种不同的转动副接触面，通过不相邻的两个顶点的转轴上的转动副接触面是不同的。
[0161]
同理，在第四个具体实施例中，当转轴通过正六面体的棱的中点时，通过在转轴上布置满足式(4)的转动副接触面，给出转动副接触面相交情况的邻接矩阵，就可以得到相应的魔方机构。这里仅给出部分模型，如图9a～9d所示，邻接矩阵不予赘述。图9a和图9b所示的魔方，12个转轴都通过棱的中点，并且同一魔方中每个转轴上的转动副接触面相同，所不同的就是转动副接触面之间的相交情况。图9c所示魔方中，正六面体棱的中点位于一个面上的转轴上的转动副接触面具有一定参数，他们之间的相交情况可以通过模型进行分析。图9d所示魔方中，每个转轴上都有两个转动副接触面，且不同转轴上这两个转动副接触面分别相同。
[0162]
综上，借助邻接矩阵可以对魔方中转动副接触面的相交情况进行相应的描述和分析，这样就可以根据转动副接触面之间邻接矩阵对应元素的值确定转动副接触面之间的相交关系，进而初步确定魔方的拓扑结构，这是本发明的重要发明点之一。
[0163]
s6、在转动副接触面相交情况确定的情况下对其相交拓扑进行分析：当魔方的转轴个数、转轴布置方式、转轴上转动副接触面和转动副接触面相交情况均相同时，分析转动副接触面相交拓扑对魔方机构拓扑结构的影响，相交的转动副接触面在魔方的外表面有相
交公共区域，根据这个区域是否为一个点对魔方的拓扑结构进行分析。
[0164]
当魔方机构转轴的数量和空间布置形式以及转动副接触面的对称布置和转动副接触面之间的相交情况确定之后，还需要对至少三个转动副接触面两两相交的情况进行转动副接触面相交拓扑的讨论分析。
[0165]
在一个具体实施例中，以正六面体为例，就n(n≥3)个转动副接触面的公共区域进行分情况讨论，进而得到不同拓扑结构的魔方，如图10a和10b所示。它们具有相同的转轴分布，同一个魔方中的转轴上有相同的转动副接触面，转动副接触面的相交情况及其邻接矩阵也是相同的。但是当改变转动副接触面之间相交拓扑的时候，会得到上述两种不同拓扑结构的魔方机构。
[0166]
在另一个具体实施例中，得到图11a和图11b所示的两种不同的魔方，它们的转轴都通过正六面体12条棱的中点，并且转轴都交于正六面体的中心，同一个魔方的每个转轴都有一个完全相同的转动副接触面，转动副接触面之间的相交情况也是相同的。
[0167]
综上，在魔方机构综合的过程中，对魔方机构转动副接触面的相交拓扑进行分析和判断，进而确定魔方机构的拓扑结构，这是本发明的又一重要发明点之一。
[0168]
s7、综合得到各种不同拓扑结构的魔方。
[0169]
本发明设计的一种基于对称空间多面体和邻接矩阵的魔方机构构型方法，根据魔方中转轴数量多且具有一定的对称性等特性，基于对称的空间多面体给出了魔方转轴的设计，并给出了魔方转动副接触面的布置原则，对魔方的设计奠定了基础和保障；借助邻接矩阵对魔方中转动副接触面的相交情况进行相应的描述和分析，根据转动副接触面之间邻接矩阵对应元素的值确定转动副接触面之间的相交关系，进而初步确定魔方的拓扑结构；通过对魔方机构转动副接触面的相交拓扑进行分析和判断，以进一步确定魔方机构的拓扑结构。
[0170]
本发明的魔方机构综合/设计过程中关注到了两个重要步骤，一个是基于对称空间多面体的转轴的对称性设计，一个是基于邻接矩阵的转动副接触面相交情况分析。本发明所提方法不仅更好地适应了不同构态的需求，也丰富了魔方的设计研究方案。
[0171]
最后所应说明的是：以上实施例仅以说明而非限制本发明的技术方案，尽管参照上述实施例对本发明进行了详细说明，本领域的普通技术人员应当理解：依然可以对本发明进行修改或者等同替换，而不脱离本发明的精神和范围的任何修改或局部替换，其均应涵盖在本发明的权利要求范围当中。