基于ladrc的伸缩套臂式无人机空基回收对接控制方法
技术领域
1.本发明涉及基于ladrc的伸缩套臂式无人机空基回收对接控制方法，属于无人机回收技术领域。


背景技术：

2.近年来，小型固定翼无人机凭借其体积小、速度快的特点得到各国军界的广泛关注，并被航空发达国家用于侦察、监控、突防、打击、集群协同火力打击等军事领域。但由于自身设计和作战使命限制，大多数小型固定翼无人机不具备远程作战能力，无法执行远程侦查、机动突防和敌后攻击等任务。即便采用大型运输机对其进行远程空基投放部署，由于远距离危险任务区域无可靠的陆基/舰基着陆平台，其在执行完任务后仍然面临无法有效回收的窘境。这不仅大大降低了其使用寿命，而且显著增加了作战成本。因此，在无可靠陆基/舰基回收平台情况下，如何采用大型空基回收平台飞机(以下称为母机)对小型固定翼无人机在空中进行快速、有效地回收，不仅可以实现无人机的重复使用、显著降低作战成本，而且还能为低成本无人机快速部署、机动突防、协同侦查和集群攻击等新型作战技术的发展提供技术支撑，具有重要的现实意义和可观的军事效能。
3.目前以美军“小精灵”项目为代表的空基回收方案主要有两种：拖曳缆绳
‑
浮标对接式回收、机械臂抓取式回收。其中，拖曳缆绳
‑
浮标对接式回收通过拖曳于母机的可收放缆绳
‑
浮标对接锁定无人机，并由缆绳将无人机卷收回母机机舱。该回收方式采用空中柔性对接方式，虽有效提高对接飞行安全，降低了对接事故率和无人机损伤。但由于柔性易扰缆绳
‑
浮标系统空中稳定性较差，使得对接过程较长，回收效率偏低。机械臂抓取式回收则是借助安装于母机的机械臂直接对稳定于期望位置的无人机进行硬式抓取对接，继而将其移动回收至母机机舱。此种回收方式虽避免了柔性易扰缆绳浮标系统空中稳定性差的问题，进一步提高了空基回收效率，但由于机械臂结构与尺寸限制，使得对接点距回收平台较近，对接风险稍高。因此，为使空基回收操作兼备高效性及安全性，需要提出一种新的无人机空基回收对接控制方法，在保障回收效率的同时使回收点远离母机平台，进一步降低回收风险。


技术实现要素：

4.本发明所要解决的技术问题是：提供基于ladrc的伸缩套臂式无人机空基回收对接控制方法，建立伸缩套臂回收装置仿射非线性模型，并基于此模型采用线性自抗扰技术(ladrc)设计了高抗扰对接控制方法，以实现空基回收环境扰流下伸缩套臂对接运动的精准控制，提高无人机空基回收的可靠性及回收效率。
5.本发明为解决上述技术问题采用以下技术方案：
6.基于ladrc的伸缩套臂式无人机空基回收对接控制方法，所述控制方法基于伸缩套臂式无人机空基回收装置实现，所述装置包括设置于空基回收平台飞机机舱舱尾的固定平台，所述固定平台下端连接有转动底座，所述转动底座通过可控俯仰关节与套臂连接，所
述套臂内部中空，且套装有伸缩臂，所述伸缩臂长度小于所述套臂长度，所述伸缩臂伸出末尾设有机械手；所述控制方法包括如下步骤：
7.步骤1，根据伸缩套臂式无人机空基回收装置结构及运动自由度，建立偏航、俯仰以及伸缩关节坐标系；
8.步骤2，根据关节运动效果不同，将伸缩套臂动力学模型分为偏航关节动力学方程、俯仰关节动力学方程和伸缩关节动力学方程，采用转动惯量质量投影法构建偏航关节动力学方程，采用拉格朗日方程法构建俯仰及伸缩关节动力学方程；
9.步骤3，将偏航、俯仰及伸缩关节动力学方程构成伸缩套臂三通道动力学模型，在考虑环境扰流的情况下对三通道动力学模型进行仿射非线性化处理，得到伸缩套臂三通道仿射非线性模型；
10.步骤4，针对步骤3伸缩套臂三通道仿射非线性模型中不可测瞬变扰动与空基回收环境扰流构成的系统集总扰动，构建扩张状态观测器，以重构各通道集总扰动；
11.步骤5，结合步骤4中扩张状态观测器，基于线性自抗扰技术设计伸缩套臂无人机空基回收对接控制器，实现环境扰流下伸缩套臂无人机空基回收对接控制。
12.作为本发明的一种优选方案，所述步骤1中，偏航关节坐标系为o0‑
x0y0z0，其坐标原点o0与所述转动底座中心重合，z轴方向与所述转动底座转轴方向重合，x轴与所述空基回收平台飞机航迹坐标系x轴平行，y轴与所述空基回收平台飞机航迹坐标系y轴平行，偏航关节坐标系满足右手法则；
13.俯仰关节坐标系为o1‑
x1y1z1，其坐标原点o1与所述可控俯仰关节中心重合，z轴方向为所述可控俯仰关节转轴方向，x轴方向指向所述伸缩臂伸缩方向，y轴方向依据右手法则确定；
14.伸缩关节坐标系为o2‑
x2y2z2，其坐标原点o2位于所述套臂末端中心处，其各轴方向与所述俯仰关节坐标系对应的各轴方向平行，且指向相同。
15.作为本发明的一种优选方案，所述步骤2中，采用转动惯量质量投影法构建偏航关节动力学方程，偏航关节动力学方程具体如下：
[0016][0017]
式中，m1、m2、m3、m4分别为转动底座、套臂、伸缩臂和机械手质量；r1、r2、r3分别为转动底座、套臂和伸缩臂截面半径；ξ为套臂与x0z0平面夹角；ω1为伸缩套臂偏航角速度；δ为套臂与x0y0平面夹角；l2为套臂长度；l3为伸缩臂长度；δl3为伸缩臂伸出套臂外长度；τ1为偏航关节驱动力矩；
[0018]
所述步骤2中，俯仰及伸缩关节动力学方程按照多关节机械臂的建模方法，在不求取系统内相互作用力的情况下，借助拉格朗日方程获取，俯仰及伸缩关节动力学方程具体如下：
[0019][0020][0021]
式中，ω2为伸缩套臂俯仰角速度；χ为机械手和伸缩臂组合刚体的质心位置，τ2为俯仰关节驱动力矩；f3为伸缩关节驱动力；g为重力加速度；v3为伸缩臂滑动速度；k3＝(m3+m4)。
[0022]
作为本发明的一种优选方案，所述步骤3中，在考虑空基回收环境扰流的情况下采用等效数学变换将伸缩套臂三通道动力学模型改写为仿射非线性形式，得到伸缩套臂仿射非线性模型，伸缩套臂仿射非线性模型具体形式如下：
[0023][0024]
式中，x1＝[ξ δ δl3]
t
、x2＝[ω
1 ω
2 v3]
t
均为伸缩套臂系统状态；b＝diag(b1,b2,b3)、u＝[τ
1 τ
2 f3]
t
分别为伸缩套臂系统输入矩阵及控制输入；f＝[0 f
2 f3]
t
为模型内不可测瞬变扰动；w＝[w
1 w
2 w3]
t
为空基回收环境扰流，w1＝0.25ρc
d
r2v2(l2+δl3)2sin2δsinξ，w2＝0.5ρc
d
r2v2(l2+δl3)2cosξsin3δ，w3＝0.5ρδl3c
d
r3v2cosξsin2δ，其中，ρ、c
d
、v分别为空气密度、阻力系数及空基回收平台飞机飞行速度；d＝[d
1 d
2 d3]
t
为模型内不可测瞬变扰动与空基回收环境扰流构成的系统集总扰动，d1、d2、d3分别为偏航、俯仰及伸缩通道集总扰动。
[0025]
作为本发明的一种优选方案，所述步骤4中，针对伸缩套臂三通道仿射非线性模型中不可测瞬变扰动及空基回收环境扰流构成的系统集总扰动，所构建扩张状态观测器具体如下：
[0026][0027]
式中，均为系统状态估计值，分别为ξ、δ、δl3估计值，分别为偏航角速度ω1、俯仰角速度ω2及伸缩臂滑动速度v3估计值；e
e
＝[e
e1 e
e2 e
e3
]
t
为观测器状态估计偏差，e
e1
、e
e2
、e
e3
分别为偏航、俯仰及伸缩通道观测器状态估计偏差；为系统集总扰动估计，分别为偏航、俯仰及
伸缩通道集总扰动估计；均为观测器系数，分别为三通道观测器带宽。
[0028]
作为本发明的一种优选方案，所述步骤5中，伸缩套臂无人机空基回收对接控制器具体形式如下：
[0029][0030]
式中，为伸缩套臂状态指令，分别为偏航、俯仰及伸缩通道状态指令；e
c1
＝[e
c11 e
c12 e
c13
]
t
、e
c2
＝[e
c21 e
c22 e
c23
]
t
均为系统跟踪误差，e
c11
、e
c12
、e
c13
分别为偏航、俯仰及伸缩通道跟踪误差，e
c21
、e
c22
、e
c23
分别为偏航、俯仰及伸缩通道跟踪误差微分；u
c
＝[u
c1 u
c2 u
c3
]
t
为控制输入，u
c1
、u
c2
、u
c3
分别为偏航、俯仰及伸缩通道控制输入；c1＝diag(c
11
,c
12
,c
13
)、c2＝diag(c
21
,c
22
,c
23
)为控制器系数，c
11
、c
21
为偏航通道控制器系数，c
12
、c
22
为俯仰通道控制器系数，c
13
、c
23
为伸缩通道控制器系数。
[0031]
本发明采用以上技术方案与现有技术相比，具有以下技术效果：
[0032]
本发明提供了一种基于ladrc的伸缩套臂式无人机空基回收对接控制方法，构建了伸缩套臂三通道仿射非线性模型，为后续开展空基回收伸缩套臂运动控制设计奠定了模型基础。并针对空基回收过程中存在环境扰流及模型内不可测量瞬变扰动的影响，设计了三通道扩张状态观测器，准确重构了系统不可测量集总扰动。同时，结合干扰观测技术，提出了一种基于ladrc的伸缩套臂式无人机空基回收对接控制器，有效提高了伸缩套臂运动控制精度及抗扰能力，显著提升了空基回收的效率及可靠性。
附图说明
[0033]
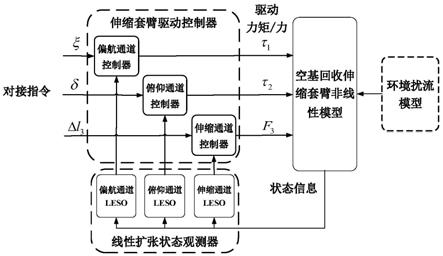
图1是本发明提供的基于ladrc的伸缩套臂式无人机空基回收对接控制方法示意图。
[0034]
图2是本发明中伸缩套臂式无人机空基回收装置整体示意图。
[0035]
其中，1
‑
母机；2
‑
固定平台；3
‑
转动底座；4
‑
可控俯仰关节；5
‑
套臂；6
‑
伸缩臂；7
‑
机械手；8
‑
待回收无人机。
[0036]
图3是本发明中扩张状态观测器集总扰动估计仿真结果图，其中，(a)是偏航关节集总扰动估计，(b)是俯仰关节集总扰动估计，(c)是伸缩关节集总扰动估计。
[0037]
图4是本发明提供的伸缩套臂对接控制方法仿真结果图，其中，(a)是偏航关节输出弧度变化，(b)是俯仰关节输出弧度变化，(c)是伸缩关节输出弧度变化。
[0038]
图5是本发明提供的伸缩套臂对接控制方法仿真结果图。
具体实施方式
[0039]
下面详细描述本发明的实施方式，所述实施方式的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施方式是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。
[0040]
本发明公开一种基于ladrc的伸缩套臂式无人机空基回收对接控制方法，首先，建立伸缩套臂非线性模型并对其进行仿射非线性处理；进而，综合考虑伸缩套臂受环境扰流及模型内不可测瞬变扰动的影响，设计扩张状态观测器，以准确重构系统内不可测集总扰动；然后，基于扩张状态观测器估计扰动，设计基于线性自抗扰技术的空基回收伸缩套臂高抗扰对接控制方法，以实现环境扰流下伸缩套臂精准对接控制。
[0041]
本实例中，设定安装有伸缩套臂的母机作定值平飞运动，飞行高度h＝3000m，飞行速度v＝100m/s，质量为136000kg，翼展为39.88m。
[0042]
如图1所示，基于ladrc的伸缩套臂式无人机空基回收对接控制方法，具体包括如下步骤：
[0043]
步骤一、根据图2所示的伸缩套臂式空基回收装置结构及运动自由度，建立偏航、俯仰、伸缩关节坐标系。
[0044]
其中，伸缩套臂式空基回收装置主要由转动底座3、可控俯仰关节4、套臂5、伸缩臂6、机械手7组成，并且整体通过固定平台2安装于母机1机身尾部。其中，转动底座3及可控俯仰关节4由液压装置进行驱动，可实现伸缩套臂自身的偏航及俯仰运动。同时，套臂5内部中空，且嵌套安装有伸缩臂6可实现回收装置伸缩运动。而机械手7则用于空基回收过程中抓取锁定待回收无人机8。
[0045]
所建关节坐标系中，o0‑
x0y0z0为偏航关节坐标系，其坐标原点与转动底座中心重合，z轴方向与转动底座转轴方向重合，x轴及y轴则分别与母机航迹坐标系x轴、y轴平行，且坐标系整体满足右手法则；o1‑
x1y1z1为俯仰关节坐标系，其坐标原点与可控俯仰关节中心重合，z轴方向为俯仰关节转轴方向，x轴方向指向伸缩臂伸缩方向，y轴方向依据右手法则确定；o2‑
x2y2z2为伸缩关节坐标系，坐标原点位于套臂末端中心处，其各轴方向与俯仰关节坐标系各轴方向平行，且指向相同；
[0046]
借助各关节坐标系齐次变换关系描述机械手运动状态，建立伸缩套臂运动学模型0p
e
：
[0047][0048]
式中：1p
e
为机械手质心在俯仰坐标系下位置；0t1为俯仰坐标系与偏航坐标系间变换矩阵；l2为套臂长度；δl3为伸缩臂伸出套臂外长度；δ为套臂与x0y0平面夹角；ξ为套臂与x0z0平面夹角；
[0049]
此步骤中，选取套臂长度l2＝8.7m。
[0050]
步骤二、根据关节运动效果不同，将伸缩套臂动力学模型分为偏航和俯仰
‑
伸缩两部分，分别采用转动惯量质量投影法及拉格朗日方程法构建；
[0051]
此步骤中，伸缩套臂偏航关节动力学方程，因偏航关节主要运动为驱动伸缩套臂整体绕转动底座进行旋转，故动力学模型可由关节驱动力矩τ1、伸缩套臂角速度ω1及转动
惯量i1表示，但由于套臂、伸缩臂及末端机械手与偏航运动转轴存在一定夹角，对应刚体转动惯量需通过质量投影法求取。而伸缩套臂俯仰及伸缩关节动力学方程可依照多关节机械臂的建模方法，在不求取系统内相互作用力的情况下，借助拉格朗日方程获取。偏航、俯仰及伸缩关节动力学模型具体如下：
[0052][0053][0054][0055]
式中：m1、m2、m3、m4分别为转动底座、套臂、伸缩臂和机械手质量；r1、r2、r3分别为转动底座、套臂和伸缩臂截面半径；l3为伸缩臂长度；ω2为伸缩套臂俯仰角速度；τ2为俯仰关节驱动力矩；v3为伸缩臂滑动速度；f3为伸缩关节驱动力；g为重力加速度；为机械手和伸缩臂组合刚体的质心位置；k3＝(m3+m4)。
[0056]
步骤三，偏航、俯仰及伸缩关节动力学方程构成伸缩套臂三通道动力学模型，在考虑环境扰流情况下采用等效数学变换将其改写为仿射非线性形式。伸缩套臂仿射非线性模型具体形式如下：
[0057][0058]
式中：x1＝[ξ δ δl3]
t
，x2＝[ω
1 ω
2 v3]
t
均为伸缩套臂系统状态；b＝diag(b1,b2,b3)，u＝[τ
1 τ
2 f3]
t
分别为伸缩套臂系统输入矩阵及控制输入；f＝[0 f
2 f3]
t
为模型内不可测瞬变扰动；w＝[w
1 w
2 w3]
t
为空基回收环境扰流，w1＝0.25ρc
d
r2v2(l2+δl3)2sin2δsinξ，w2＝0.5ρc
d
r2v2(l2+δl3)2cosξsin3δ，w3＝0.5ρδl3c
d
r3v2cosξsin2δ，其中，ρ,c
d
,v分别为空气密度、阻力系数及母机飞行速度；d＝[d
1 d
2 d3]
t
为模型内不可测瞬变扰动与空基回收环境扰流构成的系统集总扰动，d1、d2、d3分别为偏航、俯仰及伸缩通道集总扰动。
[0059]
此步骤中，选取转动底座、套臂、伸缩臂和机械手质量分别为m1＝30kg,m2＝250kg,
m3＝170kg,m4＝25kg；转动底座、套臂和伸缩臂截面半径分别为r1＝0.15m,r2＝0.1m,r3＝0.08m；伸缩臂长度l3＝8.3m；重力加速度g＝9.8；空气密度ρ＝0.73kg/m3；风阻系数c
d
＝0.2；母机飞行速度v＝100m/s。
[0060]
步骤四、针对步骤三中伸缩套臂三通道不可测瞬变模型扰动及空基回收环境扰流构成的系统集总扰动，分别构建扩张状态观测器，重构各通道集总扰动；
[0061]
此步骤中，针对伸缩套臂三通道不可测瞬变模型扰动及空基回收环境扰流构成的系统集总扰动，所构建扩张状态观测器具体如下：
[0062][0063]
式中：均为系统状态估计值，分别为ξ、δ、δl3估计值，分别为偏航角速度ω1、俯仰角速度ω2及伸缩臂滑动速度v3估计值；e
e
＝[e
e1 e
e2 e
e3
]
t
为观测器状态估计偏差，e
e1
、e
e2
、e
e3
分别为偏航、俯仰及伸缩通道观测器状态估计偏差；为系统集总扰动估计，分别为偏航、俯仰及伸缩通道集总扰动估计；均为观测器系数，分别为三通道观测器带宽；
[0064]
此步骤中，分别选取三通道观测器带宽为
[0065]
步骤五、结合步骤四中扩张状态观测器，提出一种基于ladrc的伸缩套臂式无人机空基回收对接控制器。
[0066]
该步骤中基于ladrc的伸缩套臂对接控制方法所使用控制器具体形式如下：
[0067][0068]
式中：为伸缩套臂状态指令，分别为偏航、俯仰及伸缩通道状态指令；e
c1
＝[e
c11 e
c12 e
c13
]
t
、e
c2
＝[e
c21 e
c22 e
c23
]
t
均为系统跟踪误差，e
c11
、e
c12
、e
c13
分别为偏航、俯仰及伸缩通道跟踪误差，e
c21
、e
c22
、e
c23
分别为偏航、俯仰及伸缩通道跟踪误差微分；u
c
＝[u
c1 u
c2 u
c3
]
t
为控制输入，u
c1
、u
c2
、u
c3
分别为偏航、俯仰及伸缩通道控制输入；c1＝diag(c
11
,c
12
,c
13
)，c2＝diag(c
21
,c
22
,c
23
)为控制器系数，c
11
、c
21
为偏航通道控制器系数，c
12
、c
22
为俯仰通道控制器系数，c
13
、c
23
为伸缩通道控制器系数。
[0069]
此步骤中，选取控制器具体控制系数为c1＝diag(60,50,70)；c2＝diag(80,70,90)。
[0070]
采用本发明基于ladrc的伸缩套臂式无人机空基回收对接控制方法，结合上述给定条件，在伸缩套臂起始状态为目标状态为的情况下，仿真获得观测器及对接控制结果。
[0071]
如图3中的(a)、(b)和(c)所示，为本实例所设计线性扩张状态观测器集总扰动估计结果。由图可知在回收对接过程中，伸缩套臂偏航、俯仰及伸缩关节集总扰动虽均较快变化，但所设计观测器仍能较好跟踪真实扰动，且估计偏差较小。因此，充分说明本发明所提出的线性扩张状态观测器针对伸缩套臂空基回收过程中各通道集总扰动具有较好的估计效果。
[0072]
图4
‑
5为本发明提供的伸缩套臂对接控制方法仿真结果图。由图4中的(a)、(b)和(c)可知，在所设计控制器控制下伸缩套臂各通道均能较好地跟踪对接指令，且整个过程跟踪误差较小。同时，结合图5可知回收对接过程中伸缩套臂各关节运动配合较好，对接轨迹较为平滑。因此，验证了本发明提供的伸缩套臂对接控制方法在环境扰流作用下依旧具有较好的控制效果和较高的抗扰能力。
[0073]
以上实施例仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明保护范围之内。