1.本发明属于自动化驾驶领域，具体涉及一种基于避障路径规划的无人车自适应调头控制算法。


背景技术：

2.人工智能技术开拓了一个崭新的时代，而自动驾驶是人工智能在汽车行业与交通领域的延伸与应用。现如今世界上许多国家都在积极进行智能车辆的研究和开发设计，然而无人车所带来的安全隐患也不可小觑。
3.在自动驾驶领域中，无人车的自主避障技术还有很大的发展空间，而路径规划问题是无人车避障研究中一个最为基本和关键的问题，在无人车的众多路径规划任务中，完成避障和调头任务只是其中的一部分，按照无人车所掌握的地理数据和障碍物的不同，对已知环境信息的静态障碍物进行避障路径规划已经成为各研究者的研究热点，特别是在无人车进行转弯、调头等操作时所带来的安全问题也激发了各个相关领域的研究者们的思考，在避障的同时还要不压车道线且完成调头任务的问题上仍然存在一定的困难，因此解决此问题使无人车行驶至目标领域对无人车的安全问题，路径规划问题具有重大意义。
4.为确保无人车的安全行驶，使得能够实现车道线的跟随以及避开障碍物，其转向角和车速生成的安全且平缓的行车轨迹格外重要。因此在结合无人车的位置坐标、方向角、曲率、曲率变化率、速度、加速度及运动到此点时的时间等关键参数，从而使用一种基于无人车避障路径规划的自适应车辆调头控制算法预测安全的行驶轨迹十分重要。


技术实现要素：

5.针对上述现有技术的不足：在避障的同时还要不压车道线且完成调头任务的问题上存在一定的困难，本发明提出了一种基于避障路径规划的无人车自适应调头控制算法来实现无人车在调头过程中规避障碍物的安全行驶。
6.本发明提供如下技术方案：
7.一种基于避障路径规划的无人车自适应调头控制算法，包括以下步骤：
8.s1：标定无人车行驶场地与障碍物，定义无人车控制点和解空间；
9.s2：将无人车调头的过程划分为直线行驶阶段和调头转弯阶段，将在无人车调头过程中划分为三个阶段来简化模型；
10.s3：提出基于避障路径规划的无人车自适应调头控制算法；
11.s4：结合基于避障路径规划的无人车自适应调头控制算法，使用欧拉法对无人车的直线行驶阶段和调头转弯阶段计算无人车调头路径规划轨迹；
12.s5：进行模拟仿真实验。
13.进一步地，在s1中，包括以下步骤：
14.标定无人车行驶场地与障碍物，无人车行驶场地测距，以无人车的控制点为原点，确定场地范围的四个坐标点、障碍物的四个坐标点、外车道线的两个坐标点、内车道线的两
个坐标点；
15.选取控制点，将无人车的两个前轮看作一个整体，连接两个前车轮的轴心，然然后取两点的中心点位于a点，将两个后轮看作一个整体，连接两个后车轮的轴心，取两点的中心点位于b点，取ab两点对称轴方向的中间点，将其令为c点，作为无人车的控制点；
16.定义解空间，根据障碍物和边界约束，将无人车安全轨迹限制在空间集合s中，将空间分为三个矩形部分s1,s2,s3，解空间s满足：
[0017][0018]
si＝{(x,y)|ai《x《bi,ci《y《di}。
[0019]
进一步地：在s2中，包括以下步骤：
[0020]
在直线行驶过程无人车以不超过3m/s的加速度行驶；
[0021]
将无人车调头转弯过程视为u型，在调头过程中总共分为ι、ιι、ιιι阶段；
[0022]
在ι阶段，无人车直线行驶达到速度v0开始进行方向盘的旋转；
[0023]
在ιι阶段，无人车的前轮以可变的角度行驶，直到无人车方向盘的可转动角度达到条件状态；
[0024]
在ιιι阶段方向盘的转速达到极限状态时即方向盘回正的同时车身转至指定角度完成调头。
[0025]
进一步地：在s3中，包括以下步骤：
[0026]
在无人车调头过程中的第i阶段，将无人车调头行驶简化后无人车的调头轨迹呈现u形，在这个过程中考虑两个角度的变化，其中δ
fmax
表示无人车前轮偏角达到的最大角度，δδf表示前轮偏角的变化量，ψi(i＝1,2,3)表示无人车第i阶段的ψ的偏移角度，即车身的偏角；
[0027]
由正弦法则可列等式：
[0028][0029]
展开后有：
[0030][0031]
联立后有：
[0032][0033]
由于无人车在调头行驶的整个过程中都是匀速行驶的，则设无人车的方向变化率等于车辆的角速度，则车辆的角速度有最后可得：
[0034][0035]
设方向盘的角速度为ωd，因为方向盘与前轮转角的传动比为16:1，则前轮摆动的角速度ω＝ωd/16/180*π,由于在速度保持匀速的前提条件下打方向盘的速度越小其转弯的弧度越大，即无人车在调头过程中的弯道半径越大，则引入控制无人车前轮的角速度的
可变函数控制无人车加速度的可变函数用这两个函数以此实现无人车在调头过程中自主变化方向与加速度实现路径规划完成调头任务；
[0036]
得到基于避障路径规划的无人车自适应调头控制算法，其中(xn,yn)表示无人车的调头轨迹：
[0037][0038]
在无人车调头过程中的第ii阶段，由于规定方向盘最大转角为470
°
，且方向盘与前轮转角的传动比为16:1，因此前轮转角的最大角度为29.375
°
,当前轮转动角度达到最大时即δf＝δ
fmax
则进入第二阶段，此时δf＝δ
max
,,第ii阶段模型有为：
[0039][0040]
在无人车调头过程中的第iii阶段，定义第i阶段、第ii阶段、第iii阶段的航向角偏移量为ψ1、ψ2、ψ3，为了控制在弯道后无人车沿垂直驶出，控制在第三阶段方向盘回正后航向角偏移量恰好为180
°
，即：
[0041]
ψ1+ψ2+ψ3＝180
°
[0042]
第一阶段和第三阶段由于前轮转角的角速度恒定，且速度v恒定，可以得出：
[0043]
ψ2＝180
°‑
(ψ1+ψ3)
[0044]
即第二阶段仿真时保证ψ2达到该值时，则停止迭代，进入第三阶段，第ii阶段模型为：
[0045][0046]
在第i阶段初无人车前车轮的偏角为δ
f0
＝0，在第ii阶段无人车前车轮的偏角始终保持为δ
f1
＝δ
fmax
，在第iii阶段开始回方向盘,无人车前车轮的偏角由δ
fmax
变为0，在第iii阶段末无人车的车身旋转180
°
，即航向角此时方向盘已经回正、δf＝0。
[0047]
进一步地：在s4中，主要包括以下步骤：
[0048]
结合基于避障路径规划的无人车自适应调头控制算法，使用欧拉公式进行无人车行驶轨迹求解，得：
[0049][0050]
则有初值条件v0＝0，δ
f,0
＝0，x0＝0，y0＝0，两个约束条件为：
[0051]
约束条件1：
[0052][0053]
约束条件2：
[0054][0055]
其中s为解空间。
[0056]
进一步地：步骤s5中，为使用matlab软件进行模拟仿真实验，以无人车不同初速度与角速度为特征进行模拟仿真。
[0057]
同现有技术相比，本发明具有以下有益结果：
[0058]
本发明首先在传统的单车运动算法基础上，考虑到控制车辆行驶的参数，引入了两个函数变量，包括无人车前轮角速度的可变函数以及控制无人车加速度的可变函数发明了一种基于避障路径规划的无人车自适应调头控制算法，结合euler差分迭代法求解满足规避障碍物和边界约束条件的无人车调头的行驶轨迹和相关参数，最后使用matlab软件进行了模拟仿真和可视化，仿真实验表明本发明公开的方法能够有效的完成已知环境中规避障碍物，且在不压车道线的条件下完成调头任务，证明了该发明于自动驾驶领域中提高了无人车行驶的安全性，以及在规避障碍物路径规划的调头任务中的可靠性和实用性。
附图说明
[0059]
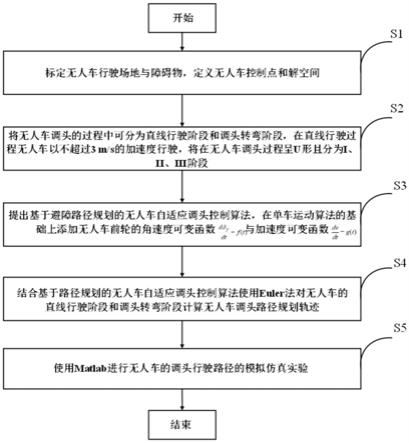
图1为本发明公开的一种可变角度的车辆控制调头模型的流程图；
[0060]
图2为控制点的选取示意图；
[0061]
图3为解空间示意图；
[0062]
图4为无人车u型调头过程场景图；
[0063]
图5为无人车可变角度的车辆控制调头模型示意图；
[0064]
图6(a)至图6(d)为matlab模拟仿真图。
具体实施方式
[0065]
下面结合附图对本发明作进一步的详细说明。
[0066]
如图1，为本发明公开的一种可变角度的车辆控制调头模型的流程图，具体包括以下步骤：
[0067]
s1：
[0068]
标定无人车行驶场地与障碍物，定义无人车控制点和解空间；
[0069]
在此步骤中，包括以下步骤：
[0070]
在本步骤s1中，包括以下具体步骤：
[0071]
s100：标定无人车行驶场地与障碍物，无人车行驶场地测距，以无人车的控制点为原点，场地范围的四个坐标点(x,y)分别为(1.5024，-4.9270)，(1.5024,26.5489)，(-13.5194，27.6157)，(-13.4342，-5.3108)，障碍物的四个坐标点分别为(-1.5024，-5.0730)，(-1.4853,10.9527)，(-3.0210,10.7992)，(-2.9785，-5.6640)，外车道线的两个
坐标点分别为(-9.9915,11.0347)，(-9.9489，-5.4286)，内车道线的两个坐标点分别为(-6.5063,10.9170)，(-6.4637，-5.5463)，无人车在此基础上行驶，规避障碍物以及完成调头任务。
[0072]
s101：选取无人车控制点，将无人车的两个前轮看作一个整体，连接两个前车轮的轴心，然后取两点的中心点位于a点，将两个后轮看作一个整体，连接两个后车轮的轴心，取两点的中心点位于b点，取a点、b点两点对称轴方向的中间点，将其令为c点，作为无人车的控制点，如图2所示。因为选取的控制点需要符合传统单车模型的中心点，所以按照上述方法选取控制点是符合要求的。
[0073]
s102：定义解空间，参阅图3，由于障碍物和边界约束，将无人车安全轨迹限制在空间集合s中，蓝色的框表示边界，将空间分为三个矩形部分s1,s2,s3，表1为解空间矩形的边界坐标，且解空间s满足：
[0074][0075]
si＝{(x,y)|ai《x《bi,ci《y《di}
[0076]
其中，ai,bi,ci,di表示第i个矩形的四个点，且有(x
l
,y
l
)∈s,(xr,yr)∈s
[0077]
表1解空间矩形的边界坐标
[0078][0079]
s2：
[0080]
将无人车调头的过程分为直线行驶阶段和调头转弯阶段，在直线行驶过程无人车以不超过3m/s的加速度行驶，将在无人车调头过程呈u形且分为i、ii、iii阶段；
[0081]
在步骤s2中，包括以下具体步骤：
[0082]
s200：将无人车的行驶过程分为直线行驶阶段和调头转弯阶段。在直线行驶过程中无人车以不超过3m/s的加速度行驶，将无人车调头转弯过程视为u型，在调头过程中总共分为ι、ιι、ιιι阶段，如图4所示，在ι阶段，无人车直线行驶达到速度v0开始进行方向盘的旋转，在ιι阶段，无人车的前轮以可变的角度行驶，直到无人车方向盘的可转动角度达到条件状态，在ιιι阶段方向盘的转速达到极限状态时即方向盘回正的同时车身转至指定角度完成调头，至此无人车实现调头过程。
[0083]
s201：考虑两个可变角度的变化。将可变角度的车辆控制模型进行简化后无人车的调头轨迹呈现u形，在这个过程中需要考虑两个角度的变化，其中δ
fmax
表示无人车前轮偏角达到的最大角度，δδf表示前轮偏角的变化量，ψi(i＝1,2,3)表示无人车第i阶段的ψ的偏移角度，即车身的偏角。
[0084]
s3：
[0085]
提出一种基于避障路径规划的无人车自适应调头控制算法，即在单车运动算法的基础上添加无人车前轮的角速度可变函数与加速度可变函数
[0086]
具体实施时，在步骤s3中，包括以下具体步骤：
[0087]
s300：在无人车调头过程中的第i阶段，以控制点为基准，如图5所示，航向角ψ由方向盘转动的角度来控制，无人车前轮转动的角速度为ω，β为滑移角。设在t0时刻小车为起始位置，在小车进行直线行驶到t1点开始进行方向盘的转动，此时的入弯速度为v0，由于无人车属于前轮转向，后轮驱动，因此在无人车调头过程中设δr恒为0。
[0088]
s301：传统的单车运动模型并没有考虑到方向盘转动的可控制性以及无人车的加速度，在此基础上在引入关于控制无人车方向盘角度随时间变化的函数f(t)从而约束无人车前轮的转动角度，以及引入关于控制无人车的加速度随时间变化的可控函数g(t)从而约束无人车在行驶过程中的速度变化。
[0089]
s302：由正弦法则可列等式：
[0090][0091]
展开可得：
[0092][0093]
联立可得：
[0094][0095]
s303：设无人车在调头行驶的整个过程中都是匀速行驶的，则此时设无人车的方向变化率等于车辆的角速度，则车辆的角速度有：
[0096][0097]
则有：
[0098][0099]
s304：设方向盘的角速度为ωd，因为方向盘与前轮转角的传动比为16:1，则前轮摆动的角速度ω＝ωd/16/180*π,由于在速度保持匀速的前提条件下打方向盘的速度越小其转弯的弧度越大，即无人车在调头过程中的弯道半径越大，则引入控制无人车前轮的角速度的可变函数控制无人车加速度的可变函数则有可变角度的车辆控制调头模型：
[0100][0101]
s305：在调头转弯的第ii阶段，由于方向盘最大转角为470
°
,且方向盘与前轮转角的传动比为16:1，因此前轮转角的最大角度为29.375
°
,当前轮转动角度达到最大时即δf＝δ
fmax
则进入第ii阶段，此时δf＝δ
max
,,则第ii阶段模型有：
[0102][0103]
s306：在无人车调头转弯中的第iii阶段。定义第i阶段，第ii阶段，第iii阶段的航向角偏移量为ψ1,ψ2,ψ3，为了控制在弯道后无人车沿垂直驶出，我们必须控制在第三阶段方向盘回正后航向角偏移量恰好为180
°
即ψ1+ψ2+ψ3＝180
°
,第一阶段和第三阶段由于前轮转角的角速度恒定，且速度v恒定，因此可以通过仿真直接计算ψ1,ψ3又因上述约束条件可以解出ψ2＝180
°‑
(ψ1+ψ3),即第二阶段仿真时保证ψ2达到该值时，则停止迭代，进入第iii阶段。则第iii阶段模型有：
[0104][0105]
s307：在oxy坐标系中δf表示无人车前轮偏转角度与车身形成的夹角，因此在第i阶段初无人车前车轮的偏角为δ
f0
＝0，在第ii阶段无人车前车轮的偏角始终保持为根据可变角度车辆调头模型在第iii阶段开始回方向盘,无人车前车轮的偏角由δ
fmax
变为0，在第iii阶段末无人车的车身旋转180
°
，即航向角此时方向盘已经回正δf＝0，最后无人车直线行驶即可。
[0106]
s4：
[0107]
结合基于避障路径规划的无人车自适应调头控制算法使用euler法对无人车的直线行驶阶段和调头转弯阶段计算无人车调头路径规划轨迹；
[0108]
具体实施时，在步骤s4中，包括以下具体步骤：
[0109]
s400：结合基于避障路径规划的无人车自适应调头控制算法，使用欧拉法求解无人车的行驶轨迹。对于可变角度的车辆控制调头模型由euler法得：
[0110][0111]
s401：有初始条件v0＝0，δ
f,0
＝0，x0＝0，y0＝0，约束条件1：
[0112][0113]
约束条件2：
[0114][0115]
其中，s为解空间。
[0116]
s402：直线行驶阶段求解。因为曲率约束入弯速度，因此，当曲率不高于0.205对应入弯速度大于1.63m/s，曲率不高于0.21对应入弯速度大于1.585m/s，最后设满足曲率的最小入弯速度v0＝1.63m/s。令无人车的加速度为a＝3m/s2做匀加速运动，在满足不触碰障碍物和边界的要求，无人车的最大行驶速度v0＝10.0519m/s，故v0最后的取值范围为(1.63,10.0519)。若要使得小车通过障碍物，由图可推测需保证小车先直线行驶到最小位移x。通过代入小车的最小入弯速度1.63m/s和方向盘最大转速为400
°
/s(此时小车过弯曲率最大半径最小)计算得到当x》10.0150m时，小车能擦边通过障碍物。假设当小车以最小入弯速度1.63m/s通过直线行驶路段，以方向盘最大转速400
°
/s入弯临界碰到外框a上边界，计算得到此时x＝21.6913m，即小车的最大直线行驶距离x＝21.6913m,故x最后的取值范围为(10.0150,21.6913)
[0117]
s403：将靠近无人车起始点的车道称为内车道，靠近边界的左边界称为外车道，中间的车道称为中车道。在极限条件下无人车车身的左边界刚好越过障碍物也会压住车道线，因此无人车无法从内车道抵达目标区域边界，可能调头轨迹只能在中车道和外车道。设无人车向左打方向盘的方向为加速度的正方向，向右则为加速度的反方向，设δt＝0.01，当t＝[0,1,2,3,4,5,6,6.18]时，其轨迹点为(xi,yi)(i＝[1:8]取整)。当入弯速度v0＝6m/s，方向盘角速度为ωd＝200时无人车的中车道轨迹线的部分结果如表2；当入弯速度v0＝6m/s，方向盘角速度ωd＝400时外车道轨迹线的部分结果如表3。
[0118]
表2无人车的中车道轨迹线结果
[0119][0120]
表3无人车的外车道轨迹线结果
[0121][0122][0123]
s5：
[0124]
使用matlab进行无人车的调头行驶路径的模拟仿真实验。
[0125]
具体实施时，在步骤s5中，包括以下具体步骤：
[0126]
s500：如图6(a)至图6(d)所示为无人车完成调头轨迹的仿真结果展示。其中蓝色的框表示是无人车调头边界，橙色和黄色的线表示外车道线和内车道线(均表示虚线)，紫色的框表示障碍物，轨道线为黑色、红色、绿色、深蓝色组成，分别表示无人车行驶直线行驶阶段，调头转弯阶段的ι、ιι、ιιι阶段。其中实线表示的无人车控制点行驶的轨迹，虚线表示
的是加上车身和障碍物必须间隔30cm的条件之后的行驶轨迹。
[0127]
图6(a)为当v0＝6m/s，ωd＝200时无人车的调头轨迹从中道线行驶至道目标区域的轨迹线，图6(b)表示当v0＝6m/s，ωd＝400时无人车的调头轨迹从中道线行驶至道目标区域的轨迹线，图6(c)表示v0＝3.4m/s，ωd＝100，直线行驶距离x＝11时的极限情况，恰在不触碰边界的条件下从外车道完成调头，图6(d)表示v0＝0.7m/s，ωd＝400，直线行驶距离x＝11时的极限情况，即刚好压到内车道线从中车道完成调头。
[0128]
从上述的轨迹和模拟仿真结果可以看出，对于本发明公开方法的一种可变角度的车辆控制调头模型在初速度分别为6m/s，6m/s，3.4m/s，0.7m/s，角速度分别为200,400,100，400的条件下，能够使无人车有效规避障碍物以及不触碰车道线的情况下完成调头转弯任务行驶至，显然，本发明公开的方法能够在自动驾驶领域无人车规避障碍物的同时完成调头任务中有较好的表现力。
[0129]
最后说明的是，以上仅是本发明优选的实施方式，需指出的是，对于本领域技术人员在不脱离本技术方案的前提下，还可以做出若干变形和改进，上述变形和改进的技术方案应同样视为落入本技术要求保护的范围。