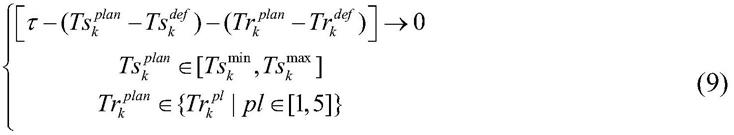
1.本发明涉及等间隔行车调整方法。


背景技术：

2.等间隔调整是一种在突发情况时使用的特殊行车指挥方式，通过合理的规划列车停站时长、运行等级，使列车之间的追踪间隔保持一致。在城市轨道交通中，若正在运营的列车发生故障，故障列车将在原地停留一段时间，待故障修复后，其它列车的早晚点现象可能非常严重，运行图严重紊乱。若车站发生火灾等自然灾害，列车无法经过该站，只能在不经过该站的小交路上行车。在这些突发情况下，列车无法按原有运行图行驶，通过等间隔调整可简单、有效地恢复运营秩序，能大大减少调度人员的工作量。
3.现有技术中存在多种等间隔调整方法，大部分方法没有考虑全体列车的分布情况，只是在局部考虑与前后几辆车的间隔，根据实际间隔和理想间隔的差异进行调整。有些现有技术既在局部考虑了前后车间隔，也根据列车群在半个交路上疏密程度，对整体分布情况进行了粗糙考虑，但方法较为复杂，实现的难度较大。还有些现有技术先选择列车数最多的区间里最中间的列车作为参考车，然后根据其它车与参考车的实际间隔和理想间隔的差异进行调整，这种方法较好地考虑了整体分布情况，但如果站台多列车少，选取的参考车不一定合适。
4.综上，目前已有的方法都没有以调整效率为优化目标，虽然能实现等间隔行车效果，但调整效率不够理想。


技术实现要素：

5.为了弥补已有方法的不足，本发明考虑了全体列车的分布情况，并以调整阶段所需的时长为优化目标，能高效地将列车群调整至等间隔行驶。
6.本发明提供了一种等间隔行车调整方法，所述方法的目标在于使每辆列车之间的追踪间隔保持一致，所述方法包括：
7.计算列车之间的追踪间隔，得到初始状态圆；
8.通过不断旋转等间隔状态圆，直至求得每辆列车的最优待调整时长；
9.通过调整停站时长和运行等级将每辆列车的最优待调整时长调整至零，以使得所述初始状态圆调整至与所述等间隔状态圆一致；
10.其中，所述初始状态圆或所述等间隔状态圆的周长表示列车按默认停站时长和默认运行时长行驶完一个交路所需的时长，在所述初始状态圆或所述等间隔状态圆的周长上设有多个圆点，每个圆点代表一辆列车，其顺时针方向的下一个圆点为其行驶方向的前一辆列车，圆点之间的弧长为列车之间按默认方式行驶的追踪间隔；
11.其中，所述初始状态圆表示初始状态列车在时间维度的相对位置，其周长上的各圆点位置通过所述计算列车之间的追踪间隔获得；所述等间隔状态圆表示等间隔行驶状态列车在时间维度的相对位置，其周长上的圆点分布均匀；
12.其中，所述待调整时长的计算方式为：列车从所述初始状态圆的对应圆点位置调整至所述等间隔状态圆上的对应圆点位置的过程中，在每个站台的停站时长和每个区间的运行时长相对于默认时长的改变量之和。
13.在一个实施例中，所述计算列车之间的追踪间隔，得到初始状态圆的步骤包括：
14.计算后车预计到达前车前方站台的时间，再计算前车预计到达其前方站台的时间，将两者相减，即为所述列车之间的追踪间隔；
15.其中，计算后车预计到达前车前方站台的时间或计算前车预计到达其前方站台的时间均采用公式(1)计算得出：
[0016][0017]
其中，tp为列车下次到达站台的预计时间，v为列车下次到达站台的编号，u为列车当前所在站台或区间编号，ts为停站时长，tr为区间运行时长，上缀plan表示计划停站时长或计划运行时长，上缀past表示已经停站时长或已经运行时长，上缀def表示默认停站时长或默认运行时长。
[0018]
在一个实施例中，规定：
[0019]
列车的数量为n，编号分别为1,2
…
n，其中2车在1车前方，3车在2车前方，以此类推；
[0020]
站台的数量为m，编号分别为1,2
…
m，每个编号对应上行或下行的一个站台，m个站台组成一个交路，其中2站在1站前方，3站在2站前方，以此类推；
[0021]
i车的待调整时长为τi，i车的待调整时长调整至零所需要的时长γi，最优待调整时长为best_τi；
[0022]
n车的前一车为1车；m站的前一站为1站；i+1表示i车或站的前一车或站；i-1表示i车或站的后一车或站；此规则同样适用于带有σ的表达式中；
[0023]
i区间表示i站至i+1站之间的区间；
[0024]
折返站的停站时长为折返时长。
[0025]
在一个实施例中，所述通过不断旋转等间隔状态圆，直至求得每辆列车的最优待调整时长的步骤包括：
[0026]
步骤501：令τ1＝0，best_τ1＝0；
[0027]
计算τ2～τn；计算γ1～γn；
[0028]
计算min_γ
max
＝max{γi|i∈[1,n]}
[0029]
步骤502：令τ1＝τ1－1；
[0030]
计算τ2～τn；计算γ1～γn；
[0031]
计算γ
max
＝max{γi|i∈[1,n]}
[0032]
步骤503：判断γ
max
是否小于min_γ
max
；
[0033]
如果γ
max
小于min_γ
max
，则令min_γ
max
＝γ
max
，best_τ1＝τ1；并返回执行步骤502；
[0034]
如果γ
max
不小于min_γ
max
，则执行步骤504；
[0035]
步骤504：令τ1＝0；
[0036]
步骤505：令τ1＝τ1+1；
[0037]
计算τ2～τn；计算γ1～γn；
[0038]
γ
max
＝max{γi|i∈[1,n]}
[0039]
步骤506：判断γ
max
是否小于min_γ
max
；如果γ
max
小于min_γ
max
，则令min_γ
max
＝γ
max
，best_τ1＝τ1，并返回执行步骤505；若γ
max
不小于min_γ
max
，则执行步骤507；
[0040]
步骤507：根据best_τ1计算best_τ2～best_τn。
[0041]
在一个实施例中，所述计算τ2～τn的方式为：
[0042]
在确定了1车的待调整时长τ1后，i车的待调整时长τi为：
[0043]
τi＝τ1+(i-1)δt
ideal-δt1→i,i∈[2,n]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0044][0045]
其中，
△
t
ideal
为理想追踪间隔，
△
t1→i为1车至i车的追踪间隔，t
period
为按默认方式行驶完一条交路所需的时长；
[0046]
所述根据best_τ1计算best_τ2～best_τn的方式与所述计算τ2～τn的方式相同。
[0047]
在一个实施例中，所述计算γ1～γn的方式为：
[0048]
若已知一列车的待调整时长τ，可估算出将该列车的待调整时长调整至零所需要的时长γ为：
[0049][0050]
其中，t
period
为按默认方式行驶完一条交路所需的时长，a
posi
和a
nega
分别为列车行驶完一条交路最多能增加和减少的停站时长以及运行时长。
[0051]
在一个实施例中，所述a
posi
和a
nega
计算方式为：
[0052][0053][0054]
其中，ts为停站时长，tr为区间运行时长式中，上缀max表示最大停站或运行时长，上缀min表示最小停站或运行时长，上缀def表示默认停站时长或默认运行时长。
[0055]
在一个实施例中，所述通过调整停站时长和运行等级将每辆列车的最优待调整时长调整至零的步骤包括：
[0056]
每次列车到达一站台时，如公式(8)更新该列车的待调整时长，且设该站台为k站：
[0057][0058]
通过公式(9)计算所述列车在k站的计划停站时长和在k区间的计划运行等级；
[0059][0060]
其中，上缀pl表示运行等级，存在5个运行等级，tr
pl
表示按该运行等级行驶所需的运行时长，ts表示停站时长，tr表示区间运行时长，上缀plan表示计划停站时长或计划运行时长，上缀real表示列车实际的停站时长或运行时长，上缀def表示默认停站时长或默认运行时长；上缀max表示最大停站或运行时长，上缀min表示最小停站或运行时长；
[0061]
计算了所述计划停站时长和所述计划运行等级后，通过自动列车监督系统将计划下发给列车执行。
[0062]
在一个实施例中，每隔一段时间重新计算各列车的所述最优待调整时长，以修正列车追踪间隔计算不准、真实停站时长或真实运行时长获取不准的系统误差。
[0063]
本发明首次将调整阶段所需的时长作为目标进行优化处理，大大提高了等间隔调整的效率。此外，本发明提出待调整时长的概率，在调整过程中，每辆列车只需将自己的待调整时长调整至零即可，无需重复计算与其它车的间隔，节省了计算资源。
附图说明
[0064]
本发明的以上发明内容以及下面的具体实施方式在结合附图阅读时会得到更好的理解。需要说明的是，附图仅作为所请求保护的发明的示例。在附图中，相同的附图标记代表相同或类似的元素。
[0065]
图1示出等间隔调整目标的抽象示意图；
[0066]
图2示出由初始状态调整至等间隔状态的示意图；
[0067]
图3示出列车编号和站台编号示意图；
[0068]
图4示出旋转等间隔状态圆对待调整时长的影响；
[0069]
图5示出根据本发明的等间隔行车调整方法的计算最优待调整时长的流程图。
具体实施方式
[0070]
以下在具体实施方式中详细叙述本发明的详细特征以及优点，其内容足以使任何本领域技术人员了解本发明的技术内容并据以实施，且根据本说明书所揭露的说明书、权利要求及附图，本领域技术人员可轻易地理解本发明相关的目的及优点。
[0071]
图1示出等间隔调整目标的抽象示意图。
[0072]
等间隔行车调整的目标是使每辆列车之间的追踪间隔保持一致，将目标抽象化表示为图1。在图1中，大圆的周长为列车按默认停站时长和默认运行时长行驶完一个交路所需的时长，一个小圆点为一辆列车，其顺时针方向的下一个圆点为其行驶方向的前一辆列车，圆点之间的边长为列车之间按默认方式行驶的追踪间隔。称图1中左圆为“初始状态圆”，表示初始状态列车在时间维度的相对位置，称右圆为“等间隔状态圆”，表示等间隔行驶状态列车在时间维度的相对位置，等间隔调整的目标就是将混乱的左圆调整至均匀分布的右圆。
[0073]
若要移动小圆点在大圆上的位置，只能通过改变停站时长和运行时长。在默认时
长的基础上，增大停站时长和运行时长，列车与前车间隔拉大，与后车间隔变小，因此小圆点逆时针移动；同理，减小停站时长和运行时长，小圆点顺时针移动。
[0074]
图2示出初始状态调整至等间隔状态的示意图。
[0075]
将初始状态圆和等间隔状态圆重叠在一起，如图2所示，可清楚地看出每辆车需要调整多少时长，才能从初始状态(实心点)变为理想等间隔状态(空心点)。
[0076]
待调整时长定义为：列车从初始状态至理想等间隔状态的过程中，在每个站台的停站时长和每个区间的运行时长相对于默认时长的改变量之和。若待调整时长为正数，则需要增加停站时长、或通过调整运行等级增加运行时长；待调整时长为负数，则需要减少停站时长、或通过调整运行等级减少运行时长；待调整时长为零，则不需要调整。
[0077]
为方便后文描述，参考图3，规定如下：
[0078]
1)列车的数量为n，编号分别为1,2
…
n，其中2车在1车前方，3车在2车前方，以此类推；
[0079]
2)站台的数量为m，编号分别为1,2
…
m，每个编号对应上行或下行的一个站台，m个站台组成一个交路，其中2站在1站前方，3站在2站前方，以此类推；
[0080]
3)n车的前一车为1车；m站的前一站为1站；i+1表示i车或站的前一车/站；i-1表示i车或站的后一车或站；此规则同样适用于σ表达式中；
[0081]
4)i区间表示i站至i+1站之间的区间；
[0082]
5)折返站的停站时长为折返时长。
[0083]
本发明的方法分为三步：
[0084]
首先，计算列车之间的追踪间隔，得到初始状态圆；其中，追踪间隔指的是间隔时长。
[0085]
然后，通过旋转等间隔状态圆，求得每辆列车的最优待调整时长；
[0086]
最后，通过调整停站时长和运行等级将每辆列车的待调整时长调整至零。
[0087]
计算列车之间的追踪间隔
[0088]
步骤“计算列车之间的追踪间隔，得到初始状态圆”描述如下。
[0089]
从自动列车监督系统(ats)中，容易获取以下信息：列车当前处于停站状态或是运行状态、所在站台/区间、计划停站/运行时长、已经停站/运行的时长、以及所有站台的默认停站时长和区间的默认运行时长。根据这些信息，可以计算出列车下次到达某站台的预计时间tp。
[0090][0091]
式(1)中，v为预计到达站台的编号，u为当前所在站台/区间编号，ts为停站时长，tr为区间运行时长，plan上缀表示计划停站/运行时长，past上缀表示已经停站/运行的时长，def上缀表示默认停站/运行时长。
[0092]
通过这种方法计算后车预计到达前车前方站台的时间，再计算前车预计到达其前方站台的时间，将两者相减，即为两车的追踪间隔。
[0093]
得到每辆车之间的追踪间隔后，假定1车位于初始状态圆的最上方，容易得到其它
列车在初始状态圆上的位置。
[0094]
计算最优待调整时长
[0095]
步骤“通过旋转等间隔状态圆，求得每辆列车的最优待调整时长”描述如下。
[0096]
图4示出旋转等间隔状态圆对待调整时长的影响。
[0097]
若将等间隔状态圆进行旋转，每辆车的待调整时长发生改变。在图4中，可直观的看出，旋转等间隔状态圆之后，大部分列车待调整时长的绝对值减小了，能更快达到等间隔效果。因此存在一个最优的理想等间隔状态(通过第一辆车的待调整时长τ1体现)，使列车群以最短的时长完成等间隔调整。
[0098]
如果确定了第一辆车的待调整时长τ1，容易知道其它车的待调整时长：
[0099]
τi＝τ1+(i-1)δt
ideal-δt1→i,i∈[2,n]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0100][0101]
其中，
△
t
ideal
为理想追踪间隔，
△
t1→i为1车至i车的追踪间隔，t
period
为按默认方式行驶完一条交路所需的时长。
[0102]
若已知列车的待调整时长τ，可估算出将该车的待调整时长调整至零所需要的时长γ：
[0103][0104]
其中a
posi
和a
nega
分别为列车行驶完一条交路最多能增加和减少的停站时长以及运行时长：
[0105][0106][0107]
式中，max上缀表示最大停站/运行时长，min上缀表示最小停站/运行时长。
[0108]
当最后一辆车的待调整时长调整至零时，列车群才实现了等间隔行驶，因此，优化目标为：
[0109]
minγ
max
＝max{γi|i∈[1,n]}
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0110]
图5示出根据本发明一实施例的等间隔行车调整方法的寻优流程图。
[0111]
步骤501：设τi表示i车的待调整时长，best_τi表示i车的最优待调整时长。
[0112]
令τ1＝0，best_τ1＝0；
[0113]
计算τ2～τn；计算γ1～γn；
[0114]
计算min_γ
max
＝max{γi|i∈[1,n]}
[0115]
步骤502：令τ1＝τ1－1；
[0116]
计算τ2～τn；计算γ1～γn；
[0117]
计算γ
max
＝max{γi|i∈[1,n]}
[0118]
步骤503：判断γ
max
是否小于min_γ
max
；如果小于，则令min_γ
max
＝γ
max
，best_τ1＝τ1(步骤508)，并返回步骤502；若不小于，则执行步骤504；
[0119]
步骤504：令τ1＝0；
[0120]
步骤505：令τ1＝τ1+1；
[0121]
计算τ2～τn；计算γ1～γn；
[0122]
γ
max
＝max{γi|i∈[1,n]}
[0123]
步骤506：判断γ
max
是否小于min_γ
max
；如果小于，则令min_γ
max
＝γ
max
，best_τ1＝τ1(步骤509)；并返回执行步骤505；若不小于，则执行步骤507；
[0124]
步骤507：根据best_τ1计算best_τ2～best_τn。所获得的最优待调整时长也就是其中，根据best_τ1计算best_τ2～best_τn的方式与计算τ2～τn的方式相同。
[0125]
调整策略
[0126]
步骤“通过调整停站时长和运行等级将每辆列车的待调整时长调整至零”描述如下。
[0127]
每次列车到达某一站台(假设为k站台)时，先更新该列车的待调整时长：
[0128][0129]
式中real上缀表示列车实际的停站/运行时长。然后通过下式计算列车在k站的计划停站时长和在k区间的计划运行等级。
[0130][0131]
式中，pl表示运行等级，假设存在5个运行等级，tr
pl
表示按该运行等级行驶所需的运行时长。计算了计划停站时长和运行等级后，通过ats将计划下发给列车执行。
[0132]
经过时间迭代，列车的待调整时长的绝对值将逐渐减小，当每辆车的待调整时长调整至零(或接近于零)时，列车群实现了等间隔行驶。
[0133]
此外，每隔一段时间，如5分钟，可按以上方法重新计算各列车的最优待调整时长，以修正列车追踪间隔计算不准、真实停站/运行时长获取不准等系统误差。
[0134]
这里采用的术语和表述方式只是用于描述，本发明并不应局限于这些术语和表述。使用这些术语和表述并不意味着排除任何示意和描述(或其中部分)的等效特征，应认识到可能存在的各种修改也应包含在权利要求范围内。其他修改、变化和替换也可能存在。相应的，权利要求应视为覆盖所有这些等效物。
[0135]
同样，需要指出的是，虽然本发明已参照当前的具体实施例来描述，但是本技术领域中的普通技术人员应当认识到，以上的实施例仅是用来说明本发明，在没有脱离本发明精神的情况下还可做出各种等效的变化或替换，因此，只要在本发明的实质精神范围内对上述实施例的变化、变型都将落在本技术的权利要求书的范围内。