1.本发明属于小型飞行器、旋翼空气动力学技术领域，尤其涉及一种全驱万向四旋翼飞行器及其控制方法。


背景技术：

2.无人机是基于无线电遥控设备或自身程序控制装置操纵来实现遥控飞行或自主飞行的无人驾驶飞行器。鉴于多旋翼飞行器具有垂直起降、空中悬停、低速飞行以及机动灵活性等优点，多旋翼飞行器被广泛地应用于森林防火、交通监控、资源勘探以及航空摄影等领域，在军事方面，常常被用于侦察探测、网络通信等极具危险性的任务。经典的多旋翼飞行器是一个欠驱动系统，因为螺旋桨产生的推力是沿着平行轴方向，为了抵消外部干扰，自身身体旋转是必需的。在某些应用中，这种限制会非常严重。


技术实现要素：

3.有鉴于此，为了填补现有技术的空白，克服现有技术中四旋翼螺旋桨的倾斜角控制的限制，避免冗余输入，本发明提供一种全驱万向四旋翼飞行器及其控制方法，将多旋翼系统的优点和全驱动无人机的敏捷性和机动性集合起来，可以解耦位置，并进行各种姿态运动，能够在任何位置和任何方向飞行。
4.其由两对旋翼组成，能够在任何位置和任何方向飞行。通过框架式的设计能够同时修改所有螺旋桨的倾斜角，从而解耦位置和姿态运动。在机架上安装了四个转子，通过两个转动接头转动机架，实现了两轴(滚动和俯仰)框架机构。这样就避免了采用复杂的闭链机构。这种解决方案不同于其他倾斜螺旋桨的全驱动uav，它避免了由于螺旋桨轴不平行而产生的内力和能量耗散。具有抵消水平面扰动的能力，提高了飞行的稳定性。特别适用于需要uav携带夹持器或机械臂来执行操作任务的应用当中。
5.本发明具体采用以下技术方案：
6.一种全驱万向四旋翼飞行器，其特征在于，包括用于安装控制组件的平台、移动框架和转子框架；所述移动框架环绕平台设置，并与平台在第一平面构成铰接；所述转子框架环绕移动框架设置，并与移动框架在第二平面构成铰接；所述第一平面和第二平面正交；四个螺旋桨分别安装在所述转子框架上。
7.其中平台一般用于承载计算硬件、电子器件和传感器等部件。
8.进一步地，所述平台与移动框架通过第一旋转接头连接，形成滚动关节轴；所述转子框架与移动框架通过与第一旋转接头正交的第二旋转接头连接，形成俯仰关节轴。通过两个转动接头转动机架，实现了两轴(滚动和俯仰)框架机构。
9.以上设计实现了：在运动过程中，飞行器通过改变转子框架的方向来产生沿任意方向的推力分量。这样，平台可以独立于转子架的任意方向。
10.进一步地，每一螺旋桨的驱动电机与所述转子框架相对固定设置。相对于现有技术，本发明通过对转子框架的控制可以同时修改所有螺旋桨的倾斜角，从而解耦位置和姿
态运动。
11.进一步地，飞行控制器由位置控制器、姿态控制器和滚距控制器组成。基于双环控制方法：外环实现位置控制器，其输出是为了实现期望的位置轨迹所需要施加到平台上的力和所述滚动关节轴的参考角度；内环根据飞行器的期望方向和所述俯仰关节轴的参考关节角度，计算关节实现期望角运动所需的力矩。
12.其可以类比现有的航空机械臂的控制方法。
13.与现有技术相比，本发明及其优选方案提供了一种全驱万向四旋翼飞行器设计方案，避免了采用复杂的闭链机构，这种解决方案不同于其他倾斜螺旋桨的全驱动uav它避免了由于螺旋桨轴不平行而产生的内力和能量耗散。具有抵消水平面扰动的能力，提高了飞行的稳定性。特别适用于需要uav携带夹持器或机械臂来执行操作任务的应用当中。
附图说明
14.下面结合附图和具体实施方式对本发明进一步详细的说明：
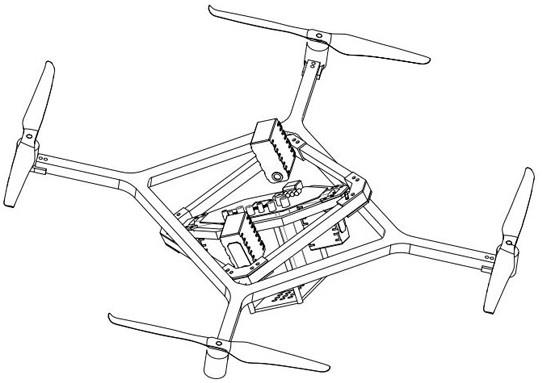
15.图1为本发明实施例全驱万向四旋翼飞行器结构示意图；
16.图2为本发明实施例全驱万向四旋翼飞行器中滚动关节轴的示意图；
17.图3为本发明实施例全驱万向四旋翼飞行器中俯仰关节轴的示意图；
18.图4为本发明实施例全驱万向四旋翼飞行器的飞行平台示意图；
19.图5为本发明实施例控制系统结构框图。
20.图中：1-平台；11-控制组件；2-移动框架；3-转子框架；4-螺旋桨。
具体实施方式
21.为让本专利的特征和优点能更明显易懂，下文特举实施例，作详细说明如下：
22.如图1-图5所示，本实施例提供的全驱万向四旋翼飞行器包括用于承载控制组件11(主要包括计算硬件、电子器件和传感器)的平台1、移动框架2和转子框架3。其中，移动框架2环绕平台设置，并与平台1在第一平面构成铰接，具体为平台1与移动框架2通过第一旋转接头连接；转子框架3环绕移动框架2设置，并与移动框架2在第二平面构成铰接第一平面和第二平面正交，具体为转子框架与移动框架通过与第一旋转接头正交的第二旋转接头连接；四个螺旋桨4分别安装在转子框架3上。
23.通过两个转动接头转动机架，实现了两轴(滚动和俯仰)框架机构。在运动过程中，飞行器通过改变转子框架3的方向来产生沿任意方向的推力分量。这样，平台1则可以独立于转子架3的任意方向。
24.每一螺旋桨4的驱动电机与转子框架3相对固定设置，因此其倾斜角度完全由转子框架3决定。相对于现有技术，本实施例通过对转子框架3的控制可以同时修改所有螺旋桨4的倾斜角，从而解耦位置和姿态运动。
25.对于控制部分，如图5所示，本实施例飞行控制器由位置控制器、姿态控制器和滚距控制器组成。基基于双环控制方法：外环实现位置控制器，其输出是为了实现期望的位置轨迹所需要施加到平台上的力和万向节的参考角度；内环根据飞行器的期望方向和参考关节角度，计算关节实现期望角运动所需的力矩。其可以类比现有的航空机械臂的控制方法。
26.本实施例提供下述基于全驱动全驱万向四旋翼飞行器的动力模型作为具体的控
制方案。
27.建立惯性坐标系σ{o,x,y,z}；
28.坐标系σ0{o0,x0,y0,z0}与平台相连，其轴x0与滚动接头轴重合；
29.坐标系σ1{o1,x1,y1,z1}，连接到移动框架上，使x1轴与节距轴重合；
30.坐标系σ2{o2,x2,y2,z2}，以这样的方式连接到转子框架，轴x1与x2重合。
31.∑0，∑1和∑2被选为o0≡o1≡o2。坐标系之间的相对方向由下列旋转矩阵给出:
[0032][0033][0034]
其中α为俯仰角，α为横摇角，c
α
＝cosα，s
α
＝sinα，c
β
＝cosβ，s
β
＝sinβ，表示σi到σj的方向。
[0035]
根据欧拉-拉格朗日公式，推导出系统的动力学模型：
[0036][0037][0038][0039]
其中p0∈ir3为o0相对于惯性系的位置，φ0＝[φ θ ψ]
t
∈ir3为欧拉角向量(如滚动-俯仰-偏转角)，α＝[α β]
t
∈ir2为万向节位置。
[0040]
将坐标系∑c0附在平台的质心c0上，并且与∑0具有相同的方向。c0相对于惯性系的位置可以表示为:
[0041][0042]
其中r0为表示平台相对于惯性系的姿态的旋转矩阵，r0为向量，c0为c0相对于o0的位置，表达式为∑0。通过微分(6)，得到∑c0的线速度和角速度:
[0043][0044]
其中是坐标系∑
*
(*＝c0,0),的角速度，在惯性坐标系中表示，s(.)是执行叉乘[17]的斜对称算子。式(7)可以用广义坐标表示为：
[0045][0046]
其中雅可比矩阵和由：
[0047][0048][0049]
t(φ0)是欧拉角的导数φ0与角速度的关系矩阵，i3、o3分别是(3
×
3)单位
矩阵和零矩阵，o3是(3
×
1)零向量。
[0050]
考虑一个坐标系∑c1，附加在移动坐标系的质心c1上，并且与∑1具有相同的方向。质心c1的位置，在惯性系中可以表示为:
[0051][0052]
其中向量r1,c1表示c1相对于01的位置，表达式为∑1；；是表示∑1与相对于惯性系方向的旋转矩阵。由于o1≡o0，(11)可以写成:
[0053][0054]
∑c1的线速度和角速度由：
[0055][0056]
当
[0057][0058]
jacobian矩阵和由:
[0059][0060][0061]
其中x0是r0的第一列。
[0062]
考虑一个坐标系∑c2它附着在转子坐标系的质心c2上，并且与∑2具有相同的方向。c2的位置在惯性系中可以表示为:
[0063][0064]
其中向量c2表示c2相对于o2的位置，表达式为∑2；而；而表示∑2相对于惯性系的方向。由于o2≡o0,(17)可以写成:
[0065][0066]
∑2的线速度和角速度是由：
[0067][0068]
其中x1是r1的第一列，雅可比矩阵和由:
[0069]
[0070]
第i个物体(i＝0,1,2)的动能t由：
[0071][0072]
其中mi质量，是惯性系中表示的惯性张量，mi是∑i中表示的惯性张量。
[0073]
第i个物体(i＝0,1,2)的势能u可以写成：
[0074][0075]
这里为重力加速度矢量。
[0076]
通过(3)(22)(23)，动态模型可以写成紧凑形式为：
[0077][0078]
m(q)∈ir8×8惯性矩阵：
[0079][0080]
科里奥利和离心项：
[0081][0082]
g(q,)∈ir8包含广义引力:
[0083][0084]
是在低速时收集摩擦力和空气动力学扰动的术语。向量ζ收集作为输入的外部广义力，即:
[0085][0086]
其中f0和μ0分别为作用在平台上的力和力矩，τ
δ
∈ir2为作用在万向节上的力矩。力f0取决于四个螺旋桨的推力，σi(i＝1,
…
4)。这样的推力是沿着z2轴方向的，因此作用在平台上的总力(∑2)有以下表达式:利用f0可以表示为:
[0087][0088][0089]
其中，μ2为框架∑2中螺旋桨产生的力矩。和μ2可以表达为:
[0090]
[0091]
其中l》0为每个电机到原点o2的距离，c＝γd/γ
t
，其中γd和γ
t
分别为阻力系数和推力系数。力矩矢量τ
δ
由关节执行器τc所产生的力矩和推力对关节的影响之和给出:
[0092][0093][0094]
出于控制设计的目的，(24)中的矩阵可以写成块矩阵：
[0095][0096]
其中m
pp
∈ir3×3,m
pφ
∈ir3×3,m
pδ
∈ir3×2,m
φφ
∈ir3×3,m
φδ
∈ir3×3和m
δδ
∈ir2×2和：
[0097][0098]cp
∈ir3×8,c
φ
∈ir3×8,c
δ
∈ir2×8,f
p
∈ir3×8,f
φ
∈ir3×8f
δ
∈ir2×8g
p
∈ir3[0099]gφ
∈ir3,g
δ
∈ir2[0100]
块分解允许重新安排动态模型(24)为:
[0101][0102]
控制目标是跟踪平台的理想位置和姿态轨迹(即坐标系∑0)，分别由向量p
0d,
(t)和φ
0d,
(t)表示以及相应的速度和加速度,
[0103]
位置控制器的控制方法：
[0104]
位置控制器是基于现有的逆动力学方法，旨在实现闭环动力学的全局线性化。为此目的，将对平台施加的命令力计算为：
[0105][0106]
假设和f
p
能够被忽略，因为通常，没有实验证明它是不可用的。这一假设在实践中得到了极好的近似验证，可以使内外环解耦。辅助输入γ
*
＝(*＝p,φ)计算为:
[0107][0108][0109]
姿态和滚距控制器的控制方法；
[0110]
力f0,与在惯性坐标系中表示的施加到平台上的控制输入一致。为了计算参考的
滚距角值，需要在∑0框架中表示控制输入，即并根据(29)将其与四个螺旋桨提供的命令总力联系起来。因此：
[0111][0112]
由(1)和(2)可以得出：
[0113][0114]
因此，期望的关节角和螺旋桨提供的总推力可以计算为：
[0115][0116][0117][0118]
关节的期望速度和加速度可以通过数值微分得到。由于在实际应用中，α和β受噪声的影响较大，因此需要使用合适的鲁棒噪声滤波器来计算所需的速度和加速度。采用时变滤波器来计算参考值的一阶和二阶时间导数。
[0119]
用于平台的命令力矩和关节力矩可按(34)计算：
[0120][0121]
其中辅助输入γδ被计算为
[0122][0123]
具有k
d,δ
，k
p,δ
和k
i,δ
ki对称和正定增益矩阵。值得注意的是，由于与f
p
相同的原因，f
φ
和f
δ
被忽略了。
[0124]
根据式(30)，可计算出四个螺旋桨所能提供的指令总力矩：
[0125][0126]
最后，通过(31)可以获得转子推力：
[0127][0128]
本专利不局限于上述最佳实施方式，任何人在本专利的启示下都可以得出其它各种形式的全驱万向四旋翼飞行器及其控制方法，凡依本发明申请专利范围所做的均等变化与修饰，皆应属本专利的涵盖范围。