一种抛物面体制星载sar场景匹配模式卫星控制方法
技术领域
1.本发明属于合成孔径雷达(synthetic aperture radar，简称sar)技术领域，尤其涉及一种抛物面体制星载sar场景匹配模式卫星控制方法。


背景技术：

2.星载场景匹配sar是星载sar的一种特有的工作模式。相对于传统星载sar，星载场景匹配sar通过连续调整俯仰维、方位维波束指向，直接生成沿目标地形的测绘带，而不是传统的沿卫星轨道生成测绘带，这使得其在对某些“斜向场景”如地震带、海岸线成像时具有独特的优势。抛物面天线结构简单，易于设计且性能优越，在卫星通信、远程通信、跟踪雷达、气象雷达和成像雷达等方面获得了广泛应用。抛物面天线主要由馈源和抛物面两部分组成，通过在抛物面焦点上放置并激发馈源，形成高增益的定向波束。
3.在成像过程中，星载场景匹配sar的波束指向沿两维方向变化，导致卫星姿态变化更加复杂，姿态控制较传统模式更为困难。同时，受限于抛物面天线本身的结构，往往采用机械控制天线转角的方法来调整波束指向。因此，亟需一种适用于抛物面天线体制的星载sar场景匹配模式卫星姿态控制方法，以解决抛物面体制星载场景匹配sar模式中卫星姿态控制难的问题。


技术实现要素：

4.为解决上述问题，本发明提供一种抛物面体制星载sar场景匹配模式卫星控制方法，可精准有效的控制场景匹配模式下的卫星姿态，实现完整的回波数据获取。
5.一种抛物面体制星载sar场景匹配模式卫星控制方法，包括以下步骤：
6.s1：获取卫星轨道坐标系到卫星本体坐标系的转换矩阵h
orbit2sat
(t)如下：
7.h
orbit2sat
(t)＝h
x
(θ
dr
(n))
×
h
y
(
‑
θ
da
(n))
×
h
z
(η(t,α))
×
h
x
(β(t))
×
h
z
(
‑
θ
tilt
(t))
8.其中，其中，β(t)为t时刻的卫星下视角，θ
tilt
(t)为t时刻的斜视角在地面的投影角，α为场景匹配模式下的观测斜角，η(t,α)为t时刻且观测斜角为α时的调整角度，θ
dr
(n)为第n个子波束在距离向的偏转角度，θ
da
(n)为第n个子波束在距离向的偏转角度，h
u
(v)表示以u轴正方向为轴，沿着右手定则的正方向将坐标轴旋转v度，其中，u＝x,y,z，v＝θ
dr
(n),θ
da
(n),η(t,α),β(t),
‑
θ
tilt
(t)；
9.s2：构建以偏航
‑
俯仰
‑
滚转为姿态转序，并构建该姿态转序下的卫星轨道坐标系到卫星本体坐标系的转换矩阵l
orbit2sat
(t)如下：
[0010][0011]
其中，表示滚转角，θ＝θ(t)表示俯仰角，ψ＝ψ(t)表示偏航角；
[0012]
s3：联立转换矩阵h
orbit2sat
(t)与转换矩阵l
orbit2sat
(t)得到卫星在场景匹配模式下，姿态转序为偏航
‑
俯仰
‑
滚转时的姿态控制指令如下：
[0013][0014]
其中，l
13
(t)表示l
orbit2sat
(t)中第一行第三列的元素，l
12
(t)表示l
orbit2sat
(t)中第一行第二列的元素l
23
(t)表示l
orbit2sat
(t)中第二行第三列的元素。
[0015]
进一步地，转换矩阵h
orbit2sat
(t)的获取方法为：
[0016]
s11：获取卫星轨道坐标系到sar坐标系的转移矩阵h
orbit2sar
(t)：
[0017]
h
orbit2sar
(t)＝h
z
(η(t,α))
×
h
x
(β(t))
×
h
z
(
‑
θ
tilt
(t))
[0018]
s12：获取sar坐标系到卫星本体坐标系的转移矩阵h
sar2sat
(t)：
[0019]
h
sar2sat
(t)＝h
x
(θ
dr
(n))
×
h
y
(
‑
θ
da
(n))
[0020]
s13：转移矩阵h
orbit2sar
(t)与转移矩阵h
sar2sat
(t)相乘得到卫星轨道坐标系到卫星本体坐标系的转换矩阵h
orbit2sat
(t)。
[0021]
进一步地，η(t,α)的解算方法如下：
[0022][0023]
其中，为t0时刻且观测斜角为α时天线距离向平面与地球的交向量，t0为成像中心时刻，h
iner2orbit
(t)为地惯系到卫星轨道坐标系的转换矩阵，u
x
(t)和u
y
(t)分别为辅助向量在轨道坐标系下的x、y轴坐标。
[0024]
进一步地，θ
tilt
(t)的解算方法如下：
[0025][0026]
其中，为地惯系下波足的位置坐标，为地惯系下卫星的位置坐标，h
iner2orbit
(t)为地惯系到卫星轨道坐标系的转换矩阵，ω(t)为升交点赤经，i(t)为轨道倾角，ψ(t)为纬度幅角，k
x
(t)和k
y
(t)分别为中间向量在轨道坐标系下的x轴、y轴坐标。
[0027]
进一步地，β(t)的解算方法如下：
[0028][0029]
其中，为地惯系下波足的位置坐标，为地惯系下卫星的位置坐标。
[0030]
有益效果：
[0031]
1、本发明提供一种抛物面体制星载sar场景匹配模式卫星控制方法，给出了卫星
在场景匹配模式下，姿态转序为偏航
‑
俯仰
‑
滚转时的姿态控制指令，可精准有效的控制卫星姿态，解决了基于抛物面天线的星载场景匹配sar卫星姿态变化复杂导致的姿态控制困难问题，实现场景匹配模式下完整的回波数据获取，弥补了场景匹配模式下卫星姿态控制的技术空白。
[0032]
2、本发明提供一种抛物面体制星载sar场景匹配模式卫星控制方法，给出t时刻且观测斜角为α时的调整角度η(t,α)的解算方法，进而能够更准确且快速的获取卫星在场景匹配模式下的姿态控制指令。
附图说明
[0033]
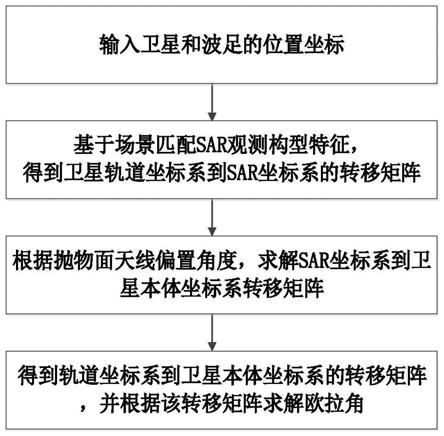
图1为本发明提供的抛物面体制星载sar场景匹配模式卫星控制方法流程图；
[0034]
图2为本发明提供的星载sar场景匹配模式观测场景；
[0035]
图3(a)为本发明提供的下视角
‑
成像时间变化曲线图；
[0036]
图3(b)为本发明提供的斜视角
‑
成像时间变化曲线图；
[0037]
图4为本发明提供的卫星三轴欧拉角
‑
成像时间变化曲线图(3
‑2‑
1转序)；
[0038]
图5为本发明提供的波足轨迹理想值与本发明设计值间的误差示意图。
具体实施方式
[0039]
为了使本技术领域的人员更好地理解本技术方案，下面将结合本技术实施例中的附图，对本技术实施例中的技术方案进行清楚、完整地描述。
[0040]
本发明提供一种适用于抛物面天线体制的星载sar场景匹配模式卫星姿态控制方法，流程图如图1所示，其具体步骤包括：
[0041]
步骤一、建立卫星轨道坐标系，卫星本体坐标系以及sar坐标系，并获取地惯系下卫星和波足的位置坐标。
[0042]
建立卫星轨道坐标系，sar坐标系以及卫星本体坐标系，其定义如下所示：卫星轨道坐标系中，x轴方向为卫星运动速度方向；z轴矢量在卫星轨道平面内且指向地心；y轴按照右手法则求解；sar天线坐标系中，x轴正方向与卫星运动方向同向，xoz面为天线沿方位向的剖面；z轴为天线波束中心指向；卫星本体坐标系的三轴矢量理论上与sar天线坐标系的三轴矢量同向，在实际工程应用中会存在少量偏移。同时，获取地惯系下卫星的位置坐标和波足的位置坐标
[0043]
步骤二、基于卫星和波足的位置坐标以及场景匹配sar观测构型特征，得到卫星轨道坐标系到sar坐标系的转移矩阵。
[0044]
场景匹配sar观测构型特征，也即卫星轨道坐标系到sar天线坐标系的转换矩阵h
orbit2sat
(t)由式(1)给出：
[0045]
h
orbit2sar
(t)＝h
z
(η(t,α))
×
h
x
(β(t))
×
h
z
(
‑
θ
tilt
(t))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0046]
其中，β(t)为t时刻卫星下视角；θ
tilt
(t)为t时刻斜视角在地面的投影角；η(t,α)为t时刻且观测斜角为α时的调整角度，保证α在成像期间保持不变；α为场景匹配模式特有的观测斜角。需要注意的是，h
x
(β(t))分别代表以x轴正方向为轴，沿着右手定则的正方向将坐标轴旋转β(t)度，h
z
(η(t,α))与h
z
(
‑
θ
tilt
(t))分别代表以z轴正方向为轴，沿着右手定则的正方向将坐标轴旋转η(t,α)度和
‑
θ
tilt
(t)度。
[0047]
θ
tilt
(t)的求解方法如式(2)所示：
[0048][0049]
其中，为地惯系下波足的位置坐标，为地惯系下卫星的位置坐标，h
iner2orbit
(t)为地惯系到卫星轨道坐标系的转换矩阵，ω(t)为升交点赤经，i(t)为轨道倾角，ψ(t)为纬度幅角，k
x
(t)和k
y
(t)分别为中间向量在轨道坐标系下的x轴、y轴坐标。
[0050]
β(t)的求解方法如式(3)所示，其正负取决于观测中卫星的左右侧视，当为右侧视时，取负值；为左侧视时，取正值：
[0051][0052]
η(t,α)的求解方法如式(4)所示：
[0053][0054]
其中，为t0时刻且观测斜角为α时天线距离向平面与地球的交向量，t0为成像中心时刻，h
iner2orbit
(t)为地惯系到卫星轨道坐标系的转换矩阵，u
x
(t)和u
y
(t)分别为辅助向量在轨道坐标系下的x、y轴坐标。
[0055]
需要说明的是，将式(2)、(3)、(4)得到的角度带入式(1)即可求解出每一时刻卫星轨道坐标系到sar坐标系的转移矩阵。
[0056]
步骤三、根据天线偏置角度，求解sar坐标系到卫星本体坐标系转移矩阵；具体的，sar天线坐标系到卫星本体坐标系的转换矩阵由式(5)给出：
[0057]
h
sar2sat
(t)＝h
x
(θ
dr
(n))
×
h
y
(
‑
θ
da
(n))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0058]
其中，θ
dr
(n)为第n个子波束在距离向的偏转角度，θ
da
(n)为第n个子波束在距离向的偏转角度；h
x
(θ
dr
(n))分别代表以x轴正方向为轴，沿着右手定则的正方向将坐标轴旋转θ
dr
(n)度，h
y
(
‑
θ
da
(n))代表以x轴正方向为轴，沿着右手定则的正方向将坐标轴旋转
‑
θ
da
(n)度。
[0059]
步骤四、依据步骤二、三，两个转换矩阵相乘可以直接求出卫星轨道坐标系到卫星本体坐标系的转换矩阵h
orbit2sat
(t)，如式(6)所示：
[0060][0061]
同时，构建轨道坐标系到卫星本体坐标系的转移矩阵l
orbit2sat
(t)，并根据该转移
矩阵求解欧拉角。具体的，对于卫星姿态控制指令来讲，一般采用欧拉角对姿态进行描述。对于相同的转移矩阵来说，不同的欧拉角转序对应不同的求解方法。本发明以3
‑2‑
1(偏航
‑
俯仰
‑
滚转)的姿态转序为例，根据该转序表示的卫星轨道坐标系到卫星本体坐标系的矩阵l
orbit2sat
(t)如式(7)所示，其中为滚转角，θ(t)为俯仰角，ψ(t)为偏航角。
[0062][0063]
其中，表示滚转角，θ＝θ(t)表示俯仰角，ψ＝ψ(t)表示偏航角。
[0064]
需要说明的是，由于公式(6)为已知量，公式(7)为未知量，两者都表示卫星轨道坐标系到卫星本体坐标系的转换矩阵，联立即可求解出卫星的3
‑2‑
1(偏航
‑
俯仰
‑
滚转)姿态控制量，如式(8)所示：
[0065][0066]
其中，l
13
(t)表示l
orbit2sat
(t)中第一行第三列的元素，l
12
(t)表示l
orbit2sat
(t)中第一行第二列的元素l
23
(t)表示l
orbit2sat
(t)中第二行第三列的元素。
[0067]
进一步地，为验证基于抛物面天线的星载场景匹配sar姿态控制方法的可行性与精确度，表1为场景匹配sar部分仿真参数，现以美国安吉利斯港及周边地区为例进行仿真验证，场景示意如图2。
[0068]
表1星载sar场景匹配模式仿真参数
[0069][0070]
基于上述场景和轨道参数，下视角及斜视角随时间变化曲线如图3(a)和图3(b)所示，可以发现在场景匹配模式下卫星下视角、斜视角均具有较大的时变，这使得卫星对波束控制精度有很高的要求；天线的三轴转角随时间变化曲线如图4所示，需要注意的是本实施例中的三轴转角是基于3
‑2‑
1转序的，其他转序下转角的求解方式与步骤四类似。为了验证该抛物面体制星载sar场景匹配模式卫星控制方法的准确性，我们给出了理想波足轨迹与该采用方法设计的波足轨迹间的误差示意如图5所示，该实施例下波束指向设计误差不超
过0.01m满足一般工程需求(在实际使用中受限于硬件精度会有一定程度的下降)。基于以上仿真结果，本专利所提的一种抛物面体制星载sar场景匹配模式卫星控制方法可精准有效的控制卫星姿态，实现完整的回波数据获取。
[0071]
当然，本发明还可有其他多种实施例，在不背离本发明精神及其实质的情况下，熟悉本领域的技术人员当然可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。