1.本发明涉及机器人控制技术领域，特别涉及一种误差矫正的地坪磨抛机器人轨迹纠偏方法及装置。


背景技术：

2.地坪磨抛机器人是一种用于地面打磨和抛光的设备，主要应用于混凝土、人造石、花岗岩、环氧地面的处理，通过高速转动的磨盘打磨地面使地面平整光滑，是地坪工程处理的主流设备。因为打磨地面平整度不一致导致打磨过程中机器人导航精度降低；地面凹陷、突起、水渍等摩擦力不一致的因素导致机器人产生跳动，主要表现为航向角偏离和横向侧滑，对机器人高精度路径导航、自主偏差轨迹纠正提出了新的挑战，研究其轨迹矫正自校正算法是提升自主导航地坪磨抛机器人导航精度的关键之一。
3.由于地面的情况复杂，外界干扰种类多，机器人实际的轨迹偏差复杂多样，因此很难确定精确的机器人数学模型，利用传统的控制理论难以应对实际机器人移动过程中的轨迹纠偏。因此，前人提出多种解决方案用于解决机器人移动过程中的轨迹偏离问题。潘世举等人提出一种基于线性时变模型预测控制的控制策略，与普通的mpc算法对比，通过仿真和实车实验证明该算法的轨迹跟踪误差在理想范围内，缺点是没有充分考虑机器人实时速度的变化，与实际运动情况存在偏差。黄刚提出一种实时修正机器人偏差的方法，并结合粒子群轨迹规划算法应用到实际的麦科勒姆轮机器人上，实现机器人快速，有效的轨迹纠偏，能够处理较小的偏差情况，美中不足的是该实验所处理的轨迹偏差值较小。s.mata、li s e等人将模型预测控制用于实际场合，考虑实际车辆运行中的情况设置控制器，具有较好的控制效果，缺点是由于车辆的运动学模型差异每次都需要重新设计控制模型。


技术实现要素：

4.本发明要解决的技术问题，在于提供一种误差矫正的地坪磨抛机器人轨迹纠偏方法及装置，实现快速修正偏移量，保证导航精度。
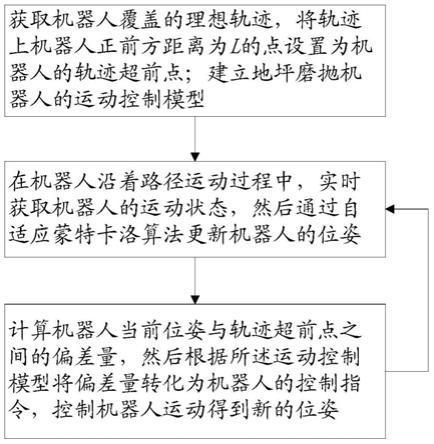
5.第一方面，本发明提供了一种误差矫正的地坪磨抛机器人轨迹纠偏方法，包括：
6.步骤10、获取机器人覆盖的理想轨迹，将轨迹上机器人正前方距离为l的点设置为机器人的轨迹超前点；建立地坪磨抛机器人的运动控制模型；
7.步骤20、在机器人沿着路径运动过程中，实时获取机器人的运动状态，然后通过自适应蒙特卡洛算法更新机器人的位姿；
8.步骤30、计算机器人当前位姿与轨迹超前点之间的偏差量，然后根据所述运动控制模型将偏差量转化为机器人的控制指令，控制机器人运动得到新的位姿，然后返回步骤20。
9.进一步地，所述步骤10中，当应用于两轮差速结构底盘的地坪磨抛机器人时，运动控制模型具体为：
[0010][0011]
其中，w表示机器人的转动角速度，v表示由驱动轮产生的前进方向速度分量，θ表示磨抛机器人在全局坐标下的方向角度，α表示地坪磨抛机器人受力方向与运动方向的夹角，f表示磨盘受到的来自地面的力，j表示地坪磨抛机器人的转动惯量，m表示地坪磨抛机器人的质量，l为超前距离。
[0012]
进一步地，所述步骤30中，计算机器人当前位姿与轨迹超前点之间的偏差量，具体为：
[0013]ex
＝x
t-xn[0014]ey
＝y
t-yn[0015][0016]
其中，e
x
代表x方向距离偏差，ey代表y方向距离偏差，e
θ
代表角度偏差，pn(xn,yn,θn)为机器人当前位姿，p
t
(x
t
,y
t
,θ
t
)为轨迹超前点。
[0017]
进一步地，所述步骤30中，将偏差量转化为机器人的控制指令，具体为：
[0018]
根据pid算法，将角度偏移量e
θ
以及x轴和y轴方向的距离偏移量e
x
、ey分别带入公式，得到两组pid输出；
[0019][0020]
其中，u(t)为偏差量修正量，k
p
为比例系数，ki为积分系数，kd为微分系数，当输入角度偏差e
θ
时输出为角度控制量，当输入为距离偏移量时输出为速度控制量。
[0021]
进一步地，所述步骤20具体为：在机器人进行正常位移时，自适应蒙特卡洛算法在原有分布的基础上叠加运动学模型更新粒子位姿；在机器人发生跳机的情况下，自适应蒙特卡洛算法重新分布粒子，开始全新一轮的迭代计算，最终得到准确表示机器人真实坐标的结果。
[0022]
第二方面，本发明提供了一种误差矫正的地坪磨抛机器人轨迹纠偏装置，包括：初始化模块、位姿更新模块以及运动控制模块；
[0023]
所述初始化模块，用于获取机器人覆盖的理想轨迹，将轨迹上机器人正前方距离为l的点设置为机器人的轨迹超前点；建立地坪磨抛机器人的运动控制模型；
[0024]
所述位姿更新模块，用于在机器人沿着路径运动过程中，实时获取机器人的运动状态，然后通过自适应蒙特卡洛算法更新机器人的位姿；
[0025]
所述运动控制模块，用于计算机器人当前位姿与轨迹超前点之间的偏差量，然后根据所述运动控制模型将偏差量转化为机器人的控制指令，控制机器人运动得到新的位姿，然后返回位姿更新模块。
[0026]
进一步地，所述初始化模块中，当应用于两轮差速结构底盘的地坪磨抛机器人时，运动控制模型具体为：
[0027][0028]
其中，w表示机器人的转动角速度，v表示由驱动轮产生的前进方向速度分量，θ表示磨抛机器人在全局坐标下的方向角度，α表示地坪磨抛机器人受力方向与运动方向的夹角，f表示磨盘受到的来自地面的力，j表示地坪磨抛机器人的转动惯量，m表示地坪磨抛机器人的质量，l为超前距离。
[0029]
进一步地，所述运动控制模块中，计算机器人当前位姿与轨迹超前点之间的偏差量，具体为：
[0030]ex
＝x
t-xn[0031]ey
＝y
t-yn[0032][0033]
其中，e
x
代表x方向距离偏差，ey代表y方向距离偏差，e
θ
代表角度偏差，pn(xn,yn,θn)为机器人当前位姿，p
t
(x
t
,y
t
,θ
t
)为轨迹超前点。
[0034]
进一步地，所述运动控制模块中，将偏差量转化为机器人的控制指令，具体为：
[0035]
根据pid算法，将角度偏移量e
θ
以及x轴和y轴方向的距离偏移量e
x
、ey分别带入公式，得到两组pid输出；
[0036][0037]
其中，u(t)为偏差量修正量，k
p
为比例系数，ki为积分系数，kd为微分系数，当输入角度偏差e
θ
时输出为角度控制量，当输入为距离偏移量时输出为速度控制量。
[0038]
进一步地，所述位姿更新模块具体为：在机器人进行正常位移时，自适应蒙特卡洛算法在原有分布的基础上叠加运动学模型更新粒子位姿；在机器人发生跳机的情况下，自适应蒙特卡洛算法重新分布粒子，开始全新一轮的迭代计算，最终得到准确表示机器人真实坐标的结果。
[0039]
本发明实施例中提供的技术方案具有如下技术效果或优点：
[0040]
本发明实施例采用超前点控制的方法能够保证机器人的轨迹偏差为正，机器人一边进行矫正一边沿着轨迹运行，接着通过自适应蒙特卡罗算法实时获取机器人位态，根据当前位姿与轨迹超前点求取偏差量，然后将偏差量解算为机器人运动控制指令，最后定位算法获取修正后的位姿，重新计算误差和控制量，形成闭环控制。本发明实施例提出的轨迹纠偏方法能够应对较大程度的偏移量，有效解决了地坪磨抛机器人的轨迹偏离问题。
[0041]
上述说明仅是本发明技术方案的概述，为了能够更清楚了解本发明的技术手段，而可依照说明书的内容予以实施，并且为了让本发明的上述和其它目的、特征和优点能够更明显易懂，以下特举本发明的具体实施方式。
附图说明
[0042]
下面参照附图结合实施例对本发明作进一步的说明。
[0043]
图1为本发明实施例一中方法的流程图；
[0044]
图2为本发明实施例一中地坪磨抛机器人控制系统流程图；
[0045]
图3为本发明实施例一中磨抛机器人运动学示意图；
[0046]
图4为本发明实施例一中偏差量计算示意图；
[0047]
图5为本发明实施例一中两次无扰动实验轨迹示意图；
[0048]
图6为本发明实施例一中扰动实验轨迹示意图；
[0049]
图7为本发明实施例一中相对实验偏差示意图；
[0050]
图8为本发明实施例一中两次干扰实验绝对偏差示意图；
[0051]
图9为本发明实施例二中装置的结构示意图。
具体实施方式
[0052]
本技术实施例通过提供一种误差矫正的地坪磨抛机器人轨迹纠偏方法及装置，实现快速修正偏移量，保证导航精度。
[0053]
本发明实施例中的技术方案，总体思路如下：
[0054]
本发明针对地坪磨抛机器人自主导航过程中抖动和跳机产生轨迹偏差的问题，提出一种基于误差量的轨迹矫正方法，解决由于地面不均匀导致机器人抖动，跳动出现大程度偏离轨迹的问题，进而实现地坪磨抛机器人的自主导航精确控制。
[0055]
首先规划地坪磨抛机器人覆盖的理想轨迹并设定轨迹超前点。然后，根据机器人当前位姿选择理想轨迹点作为跟踪目标点，通过自适应蒙特卡洛算法(adaptive deterministic monte carlo,amcl)实时获取机器人位置和姿态，从而计算目标点与机器人当前位置存在的偏差，偏差量经过距离、角度两个pid控制器解算得到电机的控制指令，控制机器人运动得到新的位姿。不断循环控制机器人循迹纠偏，实现定位到矫正的闭环系统。
[0056]
为了精准的控制机器人，纠正机器人跳机、抖动时导致轨迹偏移轨迹，本发明实施例提出一种基于误差量的轨迹纠偏方法，轨迹纠偏方法主要包括机器人定位、超前点误差计算方法、偏差量与控制指令的解算算法。
[0057]
实施例一
[0058]
本实施例提供一种误差矫正的地坪磨抛机器人轨迹纠偏方法，如图1所示，包括：
[0059]
步骤10、获取机器人覆盖的理想轨迹，将轨迹上机器人正前方距离为l的点设置为机器人的轨迹超前点；建立地坪磨抛机器人的运动控制模型；
[0060]
步骤20、在机器人沿着路径运动过程中，实时获取机器人的运动状态，然后通过自适应蒙特卡洛算法更新机器人的位姿；
[0061]
步骤30、计算机器人当前位姿与轨迹超前点之间的偏差量，然后根据所述运动控制模型将偏差量转化为机器人的控制指令，控制机器人运动得到新的位姿，然后返回步骤20。
[0062]
通过超前点控制的方法能够保证机器人的轨迹偏差为正，机器人一边进行矫正一边沿着轨迹运行，接着通过自适应蒙特卡罗算法实时获取机器人位态，根据当前位姿与轨
迹超前点求取偏差量，然后将偏差量解算为机器人运动控制指令，最后定位算法获取修正后的位姿，重新计算误差和控制量，形成闭环控制。
[0063]
本发明的方法可以适用于所有轮式结构的地坪磨抛机器人，图2是地坪磨抛机器人的控制系统流程图。首先规划地坪磨抛机器人覆盖的理想轨迹。然后，根据机器人当前位姿选择理想轨迹点作为跟踪目标点，通过自适应蒙特卡洛算法(adaptive deterministic monte carlo,amcl)实时获取机器人位置和姿态，从而计算目标点与机器人当前位置存在的偏差，偏差量经过距离、角度两个pid控制器解算得到电机的控制指令，控制机器人运动得到新的位姿。不断循环控制机器人循迹纠偏，实现定位到矫正的闭环系统。
[0064]
作为本发明的一种具体实现方式，以采用两轮差速结构底盘的地坪磨抛机器人为对象，两轮差速结构底盘包含公转的大磨盘和自转的小磨盘。其中，通过自转磨盘的相对转动平均来自地面的摩擦受力，而大磨盘的公转可以使受力出现周期性变化，减小受力不均匀的影响。
[0065]
1、地坪磨抛机器人运动控制模型
[0066]
为了分析磨抛机器人在磨抛地面时的受力情况，搭建了机器人在磨抛运动过程中的运动控制模型。磨抛机器人某一时刻，以机器人两轮中心为原点建立机器人坐标系x
c-yc，绝对坐标系x-y。如图3所示，其中θ为y和yc的夹角，机器人在全局坐标系中的姿态可表示为(x,y,θ)。对机器人受力状态展开分析，运动过程中的受力包括磨盘受力和两个驱动轮的动力。f表示磨盘受到的来自地面的力，f的大小和方向随着磨盘的转动不断发生变化，f
x
表示f垂直机器人运动方向的分量，fy表示f沿着机器人运动方向的分量。
[0067]fx
作用点与机器人的转向中心距离为l，根据刚体转动定律，受力造成机器人发生刚体转动，如公式2所示。平行于机器人运动方向的受力应用牛顿第二定律公式推导，fy产生机器人沿着机器人方向的位移动作，如公式3所示。两个力的作用效果相互叠加出现机器人发生角度改变和沿着角度方向的跳动位移。
[0068]
jω
′
＝fsinα*l
ꢀꢀꢀꢀꢀ
(1)
[0069][0070]
其中，w表示机器人的转动角速度，vy表示机器人前进方向的瞬时速度，α表示地坪磨抛机器人受力方向与运动方向的夹角，j表示地坪磨抛机器人的转动惯量，m表示地坪磨抛机器人的质量。
[0071]
磨抛机器人的运动控制模型由磨盘动力学模型叠加差速机器人运动学模型组成。差速机器人运动学模型分析需假定机器人在运动过程中不发生侧滑，此时轮子运动为纯滚动无滑动的情况，机器人运动学模型可以用速度和角速度表示，如公式3。
[0072][0073]
其中，θ表示磨抛机器人在全局坐标下的方向角度，v表示由驱动轮产生的前进方向速度分量(单位：m/s)，w表示由两驱动轮产生的角速度度(单位：rad/s)。
[0074]
综上分析，通过两轮差速模型的动力学模型公式(1)(2)叠加磨盘受力的运动学模
型公式(3)，得到地坪磨抛机器人的运动控制模型公式(4)。
[0075][0076]
其中，w表示机器人的转动角速度，v表示由驱动轮产生的前进方向速度分量，θ表示磨抛机器人在全局坐标下的方向角度，α表示地坪磨抛机器人受力方向与运动方向的夹角，f表示磨盘受到的来自地面的力，j表示地坪磨抛机器人的转动惯量，m表示地坪磨抛机器人的质量，l为超前距离。
[0077]
2、轨迹纠偏算法
[0078]
为了精准的控制机器人，纠正机器人跳机、抖动时导致轨迹偏移轨迹，本实施例提出一种基于误差量的轨迹纠偏方法，轨迹纠偏方法主要包括机器人定位、超前点误差计算方法、偏差量与控制指令的解算算法。
[0079]
2.1自适应蒙特卡洛定位
[0080]
在沿着路径运动过程中，由于地面均匀度不同，机器人自身抖动、跳动等因素，对机器人定位提出了新的挑战。传统的绝对定位方案在长距离下表现了较差的鲁棒性，如里程计时常出现信号飘移、imu产生累积误差，因此采用自适应蒙特卡洛方法(adaptive monte carlo localization,amcl)。amcl是应用广泛的激光雷达相对定位方法，分为预测阶段、测量阶段和重采样阶段，通过迭代更新粒子的方式得到机器人的准确位姿。
[0081]
预测阶段：设置粒子参数n，参数大小根据环境地图面积设定；随机散布粒子，根据机器人运动学模型和先验概率分布，随机生成n个粒子；初始时刻每一个粒子的权重如下：
[0082][0083]
所述测量阶段为：根据上一时刻粒子姿态信息和运动学模型推算产生下一时刻粒子的位姿，遍历每个粒子计算下一时刻的粒子位姿；更新粒子权重，根据建议分布函数与贝叶斯概率分布计算的后验概率密度函数的关系，利用测量数据计算粒子的权重如公式(5)。其中，p(x
k0:t
|z
1:t
,u
1:t
)表示后验概率，q(x
k0:t
|z
1:t
,u
1:t
)表示建议分布。
[0084][0085]
其中，x
tk
表示n个粒子的集合，上标k表示集合中的第k个粒子，下标t指时刻；p(z
t
|x
t
)是观测模型，表示当移动机器人姿态信息x
t
已知时，观测到z
t
的概率；p(x
t
|x
t-1
,u
t
)是运动模型，表示移动机器人在控制输入信息的作用下不同状态之间的转移概率，x
t-1
是机器人上一时刻的位姿，u
t
表示当前的控制向量，在贝叶斯理论中将这一部分描述为后验概率；分母中的q(x
t
|x
t-1
,u
t
)是p(x
t
|x
t-1
,u
t
)的理论值。
[0086]
所述重采样阶段为：根据w
tk
的大小来选择保留或者舍弃该粒子，丢弃权重小的粒子，保留权重高的粒子，并且加入随机粒子来规避粒子绑架问题，提高算法鲁棒性。经过迭代，最终粒子集中在一个区域，这个区域即机器人此时的坐标pr(xr,yr,θr)。
[0087]
自适应蒙特卡洛算法是一种相对定位的方法，利用激光雷达数据，迭代更新位姿有效避免了磨抛机器人抖动、跳机导致的定位误差累加、定位失灵的情况。正常情况下，机
器人产生位移时，算法在原有分布的基础上叠加运动学模型更新粒子位姿。在发生跳机的情况下，算法重新分布粒子，开始全新一轮的迭代计算，最终准确表示机器人真实坐标，因此之前的定位结果不会对跳机之后的定位产生影响，不会造成误差累加。
[0088]
2.2偏差量获取
[0089]
在沿着路径运动过程中，由于机器人打磨地面造成的抖动、跳动等问题，出现实际运行轨迹偏离理想轨迹的情况。不加矫正会造成后续轨迹完全偏离，导致出现更加严重的生产事故。机器人出现跳动的情况比较复杂，由于其受力方向和大小的不确定性，导致其可能发生的跳动情况比较多，可能出现前向跳机，后向跳机，侧向跳机等多种情况。为了保证在出现跳机的同时能够继续控制机器人继续沿着轨迹运行，不出现原地矫正或倒车的情况，保证控制的连续性和路径的平滑性，使用超前点控制的方法。超前点是指超前于机器人一个固定距离的路径对应点。将轨迹上机器人正前方距离为l的点设置为机器人的跟踪点，从而保证机器人跟踪点与定位点之间的误差值始终为正，能够控制机器人矫正过程中继续朝着超前点移动。
[0090]
机器人跳机的情况复杂，其中前向跳动和后向跳动的误差较为简单，最为复杂的是发生侧向跳机的情况，如图4所示。发生侧向跳机时，机器人的坐标由pr(xr,yr,θr)突变为pn(xn,yn,θn)。此时，传统的矫正方法机器人会发生原地转向调整，造成了轨迹的断续。采用超前点控制的方法能够保证机器人的轨迹偏差为正，机器人一边进行矫正一边沿着轨迹运行。此时机器人与超前点的偏差由amcl计算定位pn(xn,yn,θn)和机器人轨迹超前点p
t
(x
t
,y
t
,θ
t
)。用(e
x
,ey,e
θ
)表示机器人位置与超前点的偏差。其中：包括x方向距离偏差e
x
、y方向距离偏差ey，以及角度偏差e
θ
。
[0091]ex
＝x
t-xnꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0092]ey
＝y
t-ynꢀꢀꢀꢀꢀꢀꢀꢀ
(8)
[0093][0094]
使用当前位置与超前点的偏差计算方式，不论是出现哪种跳机工况的都能够保证偏差值为正，此时既保证了机器人运行的连续性，又保证了控制的鲁棒性。
[0095]
2.3偏移量修正
[0096]
偏移量的修正实际是将偏差量转化为机器人的控制指令，本实施例结合经典pid算法设计距离、角度控制器，如公式(10)。角度pid控制器进行机器人航向角的控制，距离pid控制器输出机器人速度指令。该控制方法将速度与角度分别控制，在误差出现时可以快速矫正，能够更加灵活的应对不同情况下的偏差。
[0097]
根据pid算法，将角度偏移量e
θ
以及x轴和y轴方向的距离偏移量e
x
、ey分别带入公式(10)，得到两组pid输出；
[0098][0099]
其中，u(t)为偏差量修正量，k
p
为比例系数，ki为积分系数，kd为微分系数，当输入角度偏差e
θ
时输出为角度控制量，当输入为距离偏移量时输出为速度控制量。
[0100]
超前点的误差计算方法有助于保证运行轨迹的平滑性，pid算法快速跟踪误差量，
两种算法保证了机器人在轨迹矫正的过程中，保证轨迹跟踪的平滑性、和误差跟踪的快速性。
[0101]
3、实验与结果分析
[0102]
轨迹矫正实验是在安装vicon光学轨迹捕捉系统的空间下进行，实现并记录机器人的移动轨迹。实验设备包含vicon光学轨迹捕捉系统和地坪磨抛机器人平台。其中，使用7个vicon光学捕捉镜头能够实时捕捉、记录空间中光学标记物的轨迹。光学反光球用于标记机器人，vicon镜头捕捉光学反光球并建立对应机器人刚体，通过刚体反应机器人姿态。7个捕捉摄像机捕捉到的位置数据通过vicon自身的交换机汇总到tracker中，tracker会对每个摄像机的数据处理然后可视化，并通过局域网共享数据，最终经过matlab、numpy进行分析处理。
[0103]
轨迹自校正实验的基本参数设置如表1所示，其中vicon光学镜头分辨率130万，频率120hz，能够捕捉高速移动目标的移动轨迹。地坪磨抛机器伺服电机额定转速3000r/min，最大线速度为每秒1m/s，最大角速度每秒1rad/s，磨盘转速每分钟2700rad/s。使用北阳激光雷达utm-30lx，有效扫描范围0.1-30m，距离分辨率0.001m，有效扫描角度270
°
，角度分辨率0.25
°
。
[0104]
表1机器人和vicon基本参数设置
[0105][0106]
3.1无扰动真值轨迹实验
[0107]
进行两组无扰动误差实验，并以第一次无扰动实验作为轨迹真值，后续实验对照均以第一组无扰动实验为基础。实验中参数设置如表2所示，设置机器人最大速度0.3m/s，机器人超前点距离为0.3m，机器人最大角速度0.25rad/s，以及相关pid参数。
[0108]
表2机器人轨迹跟踪参数设置
[0109][0110]
分别在相同实验环境下进行两次正常工况下的地坪磨抛机器人轨迹实验，测量实
验设备的误差。其中，u字形轨迹横向位移2m、纵向位移1m，记录实验轨迹如图5，机器人出发点(-1.472，-1.213)，终点(-1.618，-0.201)。实验结果可以看出，在没有扰动的情况下，两次实验的轨迹基本重合，在拐角处出现较大偏离，原因是磨抛机器人体积庞大，且转弯中心和磨盘受力点不在同一点上，属于正常现象。此时两条轨迹的偏差平均值作为对照值。
[0111]
3.2扰动实验
[0112]
地坪磨抛机器人在生产过程中，产生的跳动和角度突变处于一个较小的范围内，大约在(10，-10)的角度范围内，横向跳机小于10cm。为了测试极端情况下的轨迹矫正效果，通过人为模拟机器人受力进行两组大程度的扰动实验，第一次测试机器人在出现横向跳动的时候的矫正效果，实验中在出发0.25m处横向推动机器人，产生一个横向作用力，使机器人产生横向跳动位移，经过计算位移为22cm。第二次测试机器人在产生角度偏离时的轨迹矫正效果，在机器人出发0.5m处施加一个外力使机器人产生刚体转动，经过计算该角度偏差15度，测试其轨迹自校正能力，实验结果如图6所示。
[0113]
通过实验分析可以得到，两次扰动最终机器人都能完成轨迹的矫正，表现出较好的轨迹自校正能力，能够纠正大角度偏差和横向跳动的情况。机器人在经过直线矫正和直角转弯后基本矫正完成，此时轨迹的误差较小，机器人轨迹与无扰动轨迹贴近。在第二个拐角(0.237，-0.05104)附近由于机器人航向角未完成矫正，此时偏差增大的趋势。转弯完成后偏差逐渐减小，再经过1m的直线矫正，机器人回归轨迹，到达(-1.557，-0.163)处矫正完成，此时误差趋近于为零，后续轨迹与无扰动实验轨迹重合。
[0114]
3.3评价指标
[0115]
轨迹跟踪评估指标用机器人轨迹偏差表示。轨迹偏差指的是两条轨迹的偏离度，计算轨迹之间的偏离程度，以第一次无扰动轨迹作为轨迹真值，第二条轨迹与真值之间的欧式距离公式(11)表示。
[0116][0117]
将第一次无扰动实验作轨迹真值，求出后续三组实验对其轨迹的偏差如图7所示，实线是添加横向22cm跳动时的误差情况，点划线表示添加15度偏差时的轨迹误差情况，虚线表示第二次无扰动实验的误差情况。
[0118]
实验结果可见，无扰动实验的偏差小于0.025m。在添加扰动的一段时间内，轨迹误差持续增大，此时由于误差较大，amcl定位算法处于迭代阶段，尚未准确识别机器人位姿。后误差增加的速度快速降低，此时开始矫正轨迹，误差最大时达到0.34m，之后误差快速降低，此时机器人已经准确定位且快速矫正。当添加横向移动偏差时，机器人快速定位偏差并矫正轨迹，误差不断较小。机器人经过扰动后快速进行误差矫正，最终误差在一个较小的范围内调整，在第二个拐角后快速较小误差，最终轨轨迹矫正完成。过程中机器人经过1.5m到达第一次拐角处时误差已经小于0.05m，后续出现波动。从误差开始到矫正结束总共经过2.5m的路程，最终误差处于约等于无扰动实验误差。取轨迹稳定后的500个误差数据，计算器矫正后稳态误差数据及整个过程中最大误差如表3给出。
[0119]
表3实验误差
[0120]
组别稳态误差均值稳态最小误差稳态误差方差实验最大误差角度偏航(m)0.02880.00030.01820.3464
横向跳机(m)0.01100.00720.00440.1788无扰动(m)0.00960.00560.00120.0361
[0121]
机器人无扰动试验下其稳态误差均值为0.0096m，该误差来源于设备的不稳定性。加入横向跳机扰动后，机器人最大偏差0.1788m经过2.5m的矫正后，机器人稳态误差约0.0110m，加入角度偏航后机器人最大偏差约0.3464m，机器人经过2.5m的矫正后，稳态误差约0.0288m，矫正效果明显。
[0122]
实际工作中，在地坪磨抛机器人产生的跳动和角度突变一般处于一个较小的范围内，极少出现实验中设置的极端条件。图8为长距离下(42米)地坪磨抛机器人工作轨迹，当产生轨迹偏差时，机器人可以即时矫正位姿，整体轨迹效果较好、精度较高。因此，本实施例提出的轨迹自校正算法能够很好的解决自主导航地坪磨抛机器人实际工作中的问题。
[0123]
本实施例针对地坪磨抛机器人自主导航过程中抖动和跳机产生轨迹偏差的问题，提出一种基于误差量的轨迹矫正方法。解决由于地面不均匀导致机器人抖动，跳动出现大程度偏离轨迹的问题，进而实现地坪磨抛机器人的自主导航精确控制。为了验证算法，本实施例借助vicon光学捕捉系统进行实验，分别对机器人22cm的横向跳动，15度大角度偏差进行实验，最终经过2.5m路程的矫正后轨迹偏差小于0.03m，属于正常范围。在长距离的实际场景中，机器人也能较好地应对轨迹偏离问题。因此，本实施例提供的方法能够矫正地坪磨抛机器人自主导航过程中的轨迹偏差，具有较高导航精度。
[0124]
基于同一发明构思，本技术还提供了与实施例一中的方法对应的装置，详见实施例二。
[0125]
实施例二
[0126]
在本实施例中提供了一种误差矫正的地坪磨抛机器人轨迹纠偏装置，如图9所示，包括：初始化模块、位姿更新模块以及运动控制模块；
[0127]
所述初始化模块，用于获取机器人覆盖的理想轨迹，将轨迹上机器人正前方距离为l的点设置为机器人的轨迹超前点；建立地坪磨抛机器人的运动控制模型；
[0128]
所述位姿更新模块，用于在机器人沿着路径运动过程中，实时获取机器人的运动状态，然后通过自适应蒙特卡洛算法更新机器人的位姿；
[0129]
所述运动控制模块，用于计算机器人当前位姿与轨迹超前点之间的偏差量，然后根据所述运动控制模型将偏差量转化为机器人的控制指令，控制机器人运动得到新的位姿，然后返回位姿更新模块。
[0130]
本实施例的一种具体实现方式：
[0131]
所述初始化模块中，当应用于两轮差速结构底盘的地坪磨抛机器人时，运动控制模型具体为：
[0132][0133]
其中，w表示机器人的转动角速度，v表示由驱动轮产生的前进方向速度分量，θ表示磨抛机器人在全局坐标下的方向角度，α表示地坪磨抛机器人受力方向与运动方向的夹角，f表示磨盘受到的来自地面的力，j表示地坪磨抛机器人的转动惯量，m表示地坪磨抛机
器人的质量，l为超前距离。
[0134]
所述运动控制模块中，计算机器人当前位姿与轨迹超前点之间的偏差量，具体为：
[0135]ex
＝x
t-xn[0136]ey
＝y
t-yn[0137][0138]
其中，e
x
代表x方向距离偏差，ey代表y方向距离偏差，e
θ
代表角度偏差，pn(xn,yn,θn)为机器人当前位姿，p
t
(xt,yt,θ
t
)为轨迹超前点。
[0139]
所述运动控制模块中，将偏差量转化为机器人的控制指令，具体为：
[0140]
根据pid算法，将角度偏移量e
θ
以及x轴和y轴方向的距离偏移量e
x
、ey分别带入公式，得到两组pid输出；
[0141][0142]
其中，u(t)为偏差量修正量，k
p
为比例系数，ki为积分系数，kd为微分系数，当输入角度偏差e
θ
时输出为角度控制量，当输入为距离偏移量时输出为速度控制量。
[0143]
所述位姿更新模块具体为：在机器人进行正常位移时，自适应蒙特卡洛算法在原有分布的基础上叠加运动学模型更新粒子位姿；在机器人发生跳机的情况下，自适应蒙特卡洛算法重新分布粒子，开始全新一轮的迭代计算，最终得到准确表示机器人真实坐标的结果。
[0144]
由于本发明实施例二所介绍的装置，为实施本发明实施例一的方法所采用的装置，故而基于本发明实施例一所介绍的方法，本领域所属人员能够了解该装置的具体结构及变形，故而在此不再赘述。凡是本发明实施例一的方法所采用的装置都属于本发明所欲保护的范围。
[0145]
虽然以上描述了本发明的具体实施方式，但是熟悉本技术领域的技术人员应当理解，我们所描述的具体的实施例只是说明性的，而不是用于对本发明的范围的限定，熟悉本领域的技术人员在依照本发明的精神所作的等效的修饰以及变化，都应当涵盖在本发明的权利要求所保护的范围内。